
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Краткие теоретические сведенияСодержание книги
Поиск на нашем сайте
Таблица 2.2 – Основные законы и формулы
Алгоритм решения задач по теме: «Элементы статики»
1.Сделать рисунок, показать все силы, действующие на тело (или тела системы),находящиеся в положении равновесия, выбрать систему координат и определить направление координатных осей. 2. Для тела, не имеющего оси вращения, записать первое условие равновесия в векторной форме ∑F = 0, затем записать это условие равновесия в проекциях на оси координат и получить уравнение в скалярной форме. 3. Для тела, с закрепленной осью вращения, следует определить плечи всех сил относительно этой оси и использовать второе условие равновесия (правило моментов): ∑М = 0.Если из условия задачи следует, что ось вращения тела не закреплена, то необходимо использовать оба условия равновесия. При этом положение оси вращения следует выбирать так, чтобы через нее проходило наибольшее число линий действия неизвестных сил. 4. Решить полученную систему уравнений и определить искомые величины Примеры решения задач
1. Треугольник с углами α = 30° и β=60° составлен из легких жестких стержней, скрепленных шарнирно. Груз массой М = 2 кг подвешен так, как изображено на рисунке а. Определить силы, действующие на груз со стороны стержней. Дано: α = 30°, β=60°, М = 2 кг. Найти: F1 –? F2 –? Решение.
Рисунок 2.12 (а,б)
Укажем направления сил реакции, действующих на груз (рис. б). Запишем условие равновесия груза в векторной форме:
и в проекциях на вертикальное и горизонтальное направления:
Отсюда В подобных задачах очень часто предлагается найти силы, с которыми тело действует на связи. Решение в этом случае остается таким же: находят силы, с которыми связи действуют на тело, а потом, воспользовавшись третьим законом Ньютона, делают вывод; силы, действующие со стороны данного тела на связи, равны по модулю, противоположны по направлению щ приложены не к телу, а к связям.
Вычислим:
Ответ: 2.К вертикальной гладкой стене в точке А на веревке длиной l подвешен шар массой m (рис.). Определить силу натяжения веревки и силу давления шара на стену, если радиус шара R. Дано: l m R Найти: Т –? N –?
Рисунок 2.13 Решение. Укажем на рисунке силы, действующие на шар со стороны веревки и стены. Запишем условие равновесия шара в проекциях на горизонтальное и вертикальное направлениях:
Из рисунка 22 находим, что
а
Тогда
Силой Т шар растягивает веревку, а силой N давит на стену. Состояние равновесия – этоне обязательно состояние покоя. Из второго закона Ньютона следует: если равнодействующая приложенных к телу сил равна нулю, то тело может двигаться прямолинейно и равномерно. При таком движении тело тоже находится в состоянии равновесия. Ведь всегда можно выбрать инерциальную систему отсчета, движущуюся с такой же скоростью, в которой данное тело будет неподвижным. Например, парашютист после раскрытия парашюта опускается с постоянной скоростью и находится в состоянии равновесия. В состоянии равновесия будет и самолет, летящий прямолинейно и равномерно. Ответ: 3. Однородное бревно длиной l и массой m = 100 кг лежит на двух опорах. Расстояние от правого конца бревна до ближней опоры равно Дано: l m = 100 кг,
Найти: N1 –? N2 –? F –?
Рисунок 2.14
Решение. Выберем координатную ось так, чтобы она прошла через точку А (рис. 30). Запишем условие равновесия бревна:
где N1 и N2– силы реакции опор. Отсюда найдем:
Согласно третьему закону Ньютона бревно давит на опоры с силами Запишем теперь условие равновесия для случая, если бревно приподнято за правый конец:
Ответ: 4. Шар массой m опирается на две гладкие плоскости, образующие двугранный угол. Нижняя плоскость наклонена к горизонту под углом α, а верхняя – подуглом β к нижней (рис. 31). Определить силы давления шара на плоскости.
Дано: α β Найти: N1 –? N2 –? Решение.
Рисунок 2.15
Запишем правило моментов сил относительно точки А:
отсюда
Точно с такой же по модулю силой шар давит на верхнюю плоскость. Силу N1 определим из правила моментов сил относительно точки В:
отсюда
Точно с такой же по модулю силой шар давит на нижнюю плоскость. Ответ: 5. Цилиндр массой m = 150 кг удерживается на наклонной плоскости с помощью ленты, с одной стороны закрепленной на наклонной плоскости, а с другой направленной параллельно плоскости. Найти силу натяжения ленты. Угол наклона плоскости α = 30°. Дано: m = 150 кг, α = 30°. Найти: Т –?
Решение.
Рисунок 2.16
Задачу можно решить, применяя либо только первое условие равновесия, либо только второе. 1 способ. Используем первое условие равновесия. Запишем сумму всех действующих сил:
где Т – сила натяжения ленты, N – сила реакции опоры, mg – сила тяжести цилиндра. Возьмем проекции сил на оси ОХ и OY. Направим ось ОХ вдоль силы натяжения ленты, а ось OY перпендикулярно выбранной оси и по направлению действия силы N. На ось ОХ: 2Т – mg sinα =0 На ось OY: N – mg cosα = 0 Решая полученную систему уравнений относительно Т получим:
2 способ. Применим правило моментов относительно оси, проходящей через точку A. Момент силы тяжести M 1 = mg · d 1. Момент силы натяжения ленты M 2 = T · d 2. Плечо силы тяжести d1определим из треугольника ОАВ, где ОА= R. Угол АОВ равен углу наклона плоскости. Тогда d 1 = R · sinα. Плечо силы натяжения ленты d2 равно диаметру цилиндра или d 2 =2 R. Тогда правило моментов относительно оси А: М1 – М2=0 или mg · R · sinα – T ·2 R =0. Из данного уравнения получим:
Ответ: 6. Однородная тонкая балка АВ массой 100 кг опирается одним концом на гладкий горизонтальный пол, а другим — на гладкую плоскость, наклоненную под углом 30° к горизонту. Конец балки В поддерживается веревкой с грузом, перекинутой через блок С (см. рис.). Определить массу груза и силы нормальной реакции пола и наклонной плоскости. Трением в блоке пренебречь. Дано: m1 = 100 кг, β = 300. Найти: m2 –? Решение.
Рисунок 2.17 Рассмотрим силы, действующие на балку: m1g – сила тяжести; N1 и N 2 – силы нормальной реакции пола и наклонной плоскости; Т – сила натяжения веревки. Под действием этих сил балка находится в равновесии. Напишем для балки первое условие равновесия:
Выбрав направление осей OX и OY (как показано на рисунке) проецируем на них уравнение, получаем на ось ОХ:
на ось OY:
Запишем для балки второе условие равновесия относительно оси, проходящей через точку В: М1 – М2 = 0. Здесь M1=N1· d 1, М2=m1g· d 2 – моменты сил N1 и m1g относительно выбранной оси, где
– плечи сил N1 и m1g., где L – длина балки. Подставив выражения для М1 и М2 получим
откуда
Подставив численные данные, получим N1=490Н. Подставим полученное выражение
в уравнение
а также используя уравнение
получим:
Так как грузы находятся в равновесии, то
причем
Тогда
Подставив численные данные m 2 =25кг. Подставив значение выражения для Т найдем N 2.
Подставив численные данные N 2 =426Н. 7. Лестница длиной 4 м приставлена к идеально гладкой стене под углом 60° к горизонту. Коэффициент трения между лестницей и полом 0,33. На какое расстояние вдоль лестницы может подняться человек, прежде чем лестница начнет скользить? Массой лестницы пренебречь.
Дано: l = 4 м, α = 600, μ = 0,33. Найти: S –? Решение.
Рисунок 2.18
Обозначим все силы действующие на лестницу: N1 и N2 – силы нормальной реакции стены и пола, F – сила давления человека на лестницу; Fтp – сила трения. Скольжение лестницы можно рассматривать как совокупность двух движений: вращательного (около точки О) и поступательного (в направлении против оси X). Запишем первое условие равновесия лестницы:
Спроецируем полученное уравнение на оси OX:
и ось OY:
Запишем второе условие равновесия лестницы относительно точки О: М1 – М2 = 0, где М1= N 1 d 1 и М2= Fd 2 – моменты сил N 1 и F относительно выбранной оси, где
– плечи сил N 1 и F. Учитывая это, перепишем условие равновесия лестницы относительно точки О:
Из этого уравнения
Используя уравнения первого условия равновесия лестницы:
а также определение силы трения
найдем N 1 =μ F. Тогда, Подставляя численные данные, получаем S ≈2,3м. Ответ: S ≈2,3м
|
|||||||||||||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 178; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.107.101 (0.01 с.) |

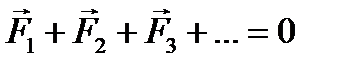
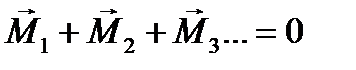
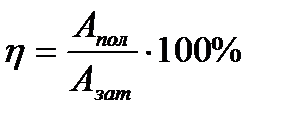


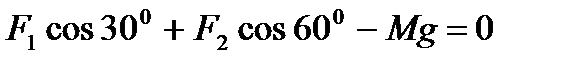 ,
, .
.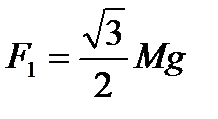 и
и 
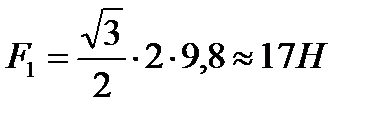
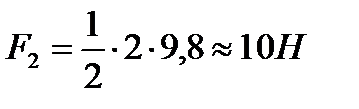
 ,
, 
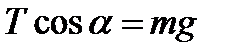 и
и 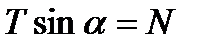 .
. ,
, .
. и
и  .
. ,
,  , а от левого -
, а от левого -  С какой силой давит бревно на каждую опору? Какую минимальную силу нужно приложить, чтобы немного приподнять бревно за правый конец?
С какой силой давит бревно на каждую опору? Какую минимальную силу нужно приложить, чтобы немного приподнять бревно за правый конец?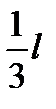 ,
, .
.
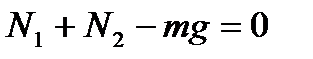 ;
;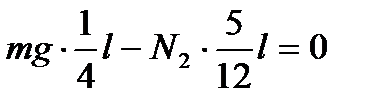
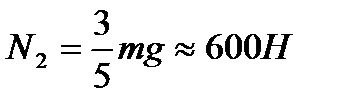 ,
,
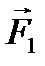 и
и  равными по модулю силам
равными по модулю силам  и
и  но противоположно направленными. Следовательно,
но противоположно направленными. Следовательно,  = 400 Н,
= 400 Н, 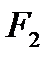 =600 Н.
=600 Н.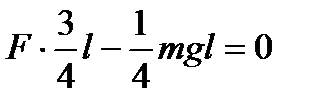 ,
,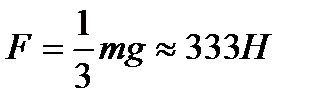
 ,
,  ,
, 
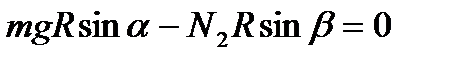

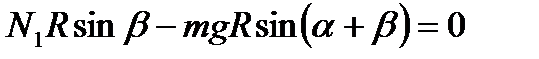 ,
,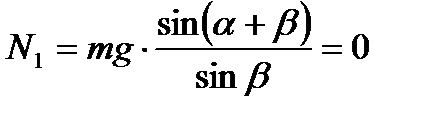
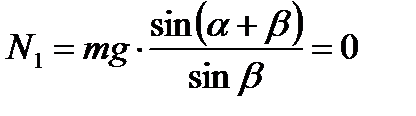 ,
,  .
.
 ,
,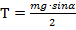 .
.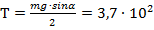 Н.
Н. Н.
Н.
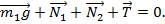
 .
.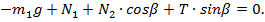
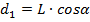 ,
,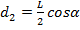
 ,
, .
. ,
, .
. ,
, .
.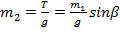 .
.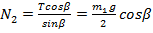 .
.



 ,
, 
 .
. .
.

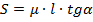 .
.


