Описание логических функций при помощи таблиц истинности.

Правило перехода от таблицы истинности к аналитической форме записи.

Для получения СКНФ выбираем случаи равенства функции нулю и записываем через И эти случай, причем, каждый случай описывается при помощи записи через ИЛИ значения аргументов функции, причем, при равенстве аргумента единице, он берется инверсным. То есть, на примере функции М2

x	y	M2
0	0	0
0	1	1
1	0	1
1	1	0

СКНФ=(A#B)& (!A#!B)

СДНФ=(!A&B)# (A&!B)

 

Доопределение функции.

Если функция

 

 

ДНФ – это такая нормальная форма, которая имеет вид дизъюнкций конъюнкций литералов.

По – русски:

 

Любые логические функции выражаются через элементарные функции булева базиса.

 

СДНФ - это такая ДНФ, которая удовлетворяет трём условиям:

§ в ней нет одинаковых элементарных конъюнкций

§ в каждой конъюнкции нет одинаковых пропозициональных букв

§ каждая элементарная конъюнкция содержит каждую пропозициональную букву из входящих в данную ДНФ пропозициональных букв, причем в одинаковом порядке.

По – русски:

 

Любая сложная функция представляется в виде (на примере двухвходовой функции M2) (!A&B)# (A&!B)

 

СКНФ

-||-, только наоборот.

По – русски:

Любая сложная функция представляется в виде (на примере двухвходовой функции M2) (A#B)& (!A#!B)

8. Логические константы и переменные. Элементы булевой алгебры. Булев базис. Взаимное преобразование логических функций(правило Де Моргана), логические элементы.

Логические константы.

Логическое выражение может быть либо истиной, либо ложью. Истине соответствует константа True, значению "ложь" - константа False.

Логические переменные.

Это переменные, принимающие только 2 значения – 1, или 0.

Элементы булевой алгебры.

Булева алгебра – формальный аппарат описания логической стороны процессов, происходящих в цифровых устройствах. Оперирует с логическими переменными.

Операции над этими переменными называются логическими операциями.

Простейшие логические операции:

НЕ

Обозначение:

Свойства:

!!a=а

И

Обозначение:

Y = a ^ b Y = ab Y = a ⋅ b Y = a & b

Свойства:

a & 0 = 0

a & 1 = a

a & a = a

a &!a = 0

Применение:

ИЛИ

Обозначение:

Y = aVb Y = a + b Y = a#b

Свойства:

a # 0 = a

a # 1 = 1

a # a = 1

a #!a = 1

Применение:

М2(исключающее ИЛИ)

Y = a ⊕ b Y = a $ b

Свойства:

а⊕0=а
а⊕1=!а

(а⊕b) ⊕b = а
!а⊕b = a⊕!b

Применение:

И-НЕ

ИЛИ – НЕ

Правило Де Моргана.

!(!a &!b) = a # b!(!a #!b) = a & b

 

Логические элементы — устройства, предназначенные для обработки информации в цифровой форме.

 

Функционально полные системы логических элементов. Синтез логических устройств в функционально полном базисе.

 

Функционально полная система логических элементов - это такой набор логических элементов, используя который, можно реализовать любую сколь угодно сложную логическую функцию. Поскольку всякая логическая функция есть комбинация простейших функций - дизъюнкции, конъюнкции и инверсии, то набор из элементов трех типов, реализующих соответственно функции И, ИЛИ и НЕ, естественно, является функционально полным.

 

ФПБ является базис И-НЕ.

Для проверки этого утверждения получим, используя только функцию И-НЕ, все функции Булева базиса.

1) ИЛИ

При соединении входов функции 2И-НЕ получаем просто НЕ (очевидно). Берется 2 элемента 2И-НЕ с соединенными входами, их выходы прикрепляются к еще одному 2И-НЕ. Получаем на выходе третьего элемента!(!A&!B), что, согласно правилу ДеМоргана = A#B, читд.

1) И

На входы 2И-НЕ подаем сигналы. На выходе имеем!(A&B). Подаем его на еще 1 элемент с соединенными входами(то есть, инвертируем)

2) НЕ

-||-

ФПБ является базис ИЛИ-НЕ.

1) ИЛИ

2) И

3) НЕ

Все функции получаются точно такой же комбинацией логических элементов, согласно правилу Де Моргана.

 

Базис Жегалкина.

Базис Жегалкина состоит из следующих логических элементов:

1) И

2) M2(Исключающее ИЛИ)

3) Константы «1»

Докажем, что он является ФПБ.

 

1) НЕ

Приведем таблицу истинности ф-и М2

x	y	M2
0	0	0
0	1	1
1	0	1
1	1	0

 

Очевидно, что при подаче на один из входов постоянной единицы, на выходе М2 присутствует сигнал, подаваемый на второй из входов, но с обратным знаком. То есть, М2 работает как инвертор.

 

2) ИЛИ

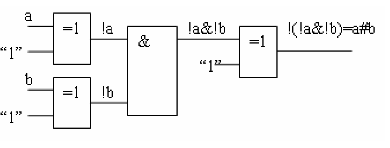
Берем два инвертора на основе M2, полученных выше, пихаем их выходы на вход функции И, после чего ставим еще один такой инвертор. В результате получаем!(!A&!B), по ДеМоргану = A#В, читд.

 

3) И

Уже есть в базисе.