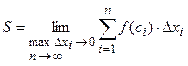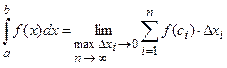Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование рациональных дробей методом неопределённых коэффициентовСодержание книги
Поиск на нашем сайте
Теорема. Всякая правильная дробь
При этом простейшими рациональными дробями называют дроби вида: Неизвестные постоянные Пример 14. Найти неопределённый интеграл Решение. Выпишем подынтегральную дробно-рациональную функциюи представим её как сумму двух простейших дробей. Чтобы не мучиться с запоминанием формулы, приведённой в теореме в начале параграфа, можно запомнить простое правило: при разложении многочлен числителя простейшей дроби должен быть на порядок меньше многочлена её знаменателя. Тогда:
Приводим правую часть равенства к общему знаменателю:
Так как знаменатели у обеих полученных рациональных дробей равны, для выполнения равенства должны быть равны и числители. Приравниваем их:
Неизвестные коэффициенты А, В и С находим способом частных значений, задаваясь значениями х и подставляя их в левую и правую части равенства:
Нам требуется решить систему уравнений:
Если для нахождения коэффициентов А, В и С использовать способ сравнения коэффициентов, то в исходном равенстве желательно раскрыть скобки:
Теперь выписываем коэффициенты, стоящие при одинаковых степенях х:
Как видим, нам придётся решить более сложную систему уравнений, чем в предыдущем случае, но результат вычислений полностью совпадает со сделанными ранее. Итак, коэффициенты найдены, можем вернуться к интегралу:
Неберущиеся» неопределённые интегралы
___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Часть 2. Определённый интеграл Задача о вычисление площади криволинейной трапеции, приводящая к понятию определенного интеграла
____________________________________________________________ ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Как найти площадь криволинейной трапеции?
Постановка задачи.________________________________________________________________________ ___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
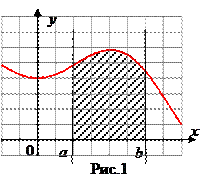
(В первом приближении)_____________________________ ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
(Во втором приближении) ____________________________ ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
(Переход к интегральной сумме)_______________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ *) Аппроксим а ция, замена одних математических объектов другими, в том или ином смысле близкими к исходным.
(Получаем точное значение)_______________________________________________________________ ___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
(2)
Обобщим полученный предел на любую непрерывную на отрезке [ a; b ] функцию.
Определение определённого интеграла. ____________________________________________________ ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
(3)
Здесь числа a и b называются ________________________________________________________________ _________________________________________________________________________________________ отрезок [ a; b ] называется ___________________________________________________________________
|
||||||||||||||
|
Последнее изменение этой страницы: 2019-12-14; просмотров: 150; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.104.121 (0.01 с.) |

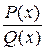 может быть представлена в виде суммы конечного числа простейших дробей:
может быть представлена в виде суммы конечного числа простейших дробей: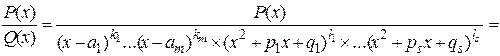

 .
.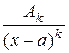 и
и 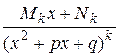 , где
, где  ,
, 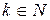 ,
, 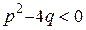 .
.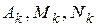 находят методом неопределённых коэффициентов, включающий два равносильных способа: сравнение коэффициентов и способ частных значений. В зависимости от задачи эти способы можно применять как по отдельности, так и комбинировать. Разберём их непосредственно на примере.
находят методом неопределённых коэффициентов, включающий два равносильных способа: сравнение коэффициентов и способ частных значений. В зависимости от задачи эти способы можно применять как по отдельности, так и комбинировать. Разберём их непосредственно на примере.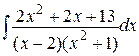 , разложив подынтегральную функцию на простейшие дроби.
, разложив подынтегральную функцию на простейшие дроби. .
.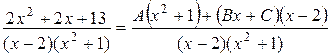 .
.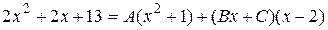 .
.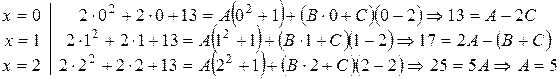
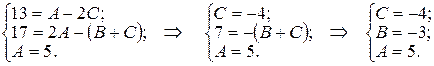
 .
.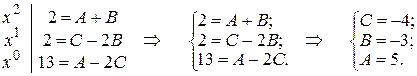
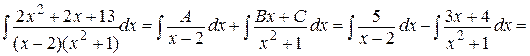
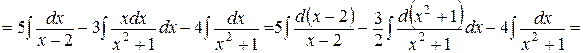
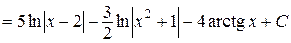 .
. Определение криволинейной трапеции.
Определение криволинейной трапеции.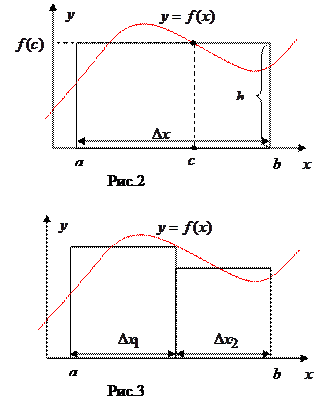
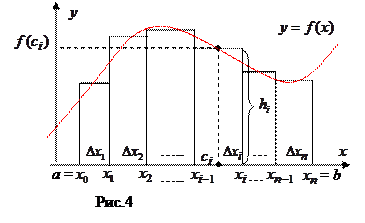 ____________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________