Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные шаги метода переменного многогранника Нелдера-Мида.Содержание книги
Поиск на нашем сайте
1) «Подготовка». Вначале выбирается 2) «Сортировка». Из вершин симплекса выбираем три точкиx h {\displaystyle x_{h}} 3) Нахождение центра тяжести всех точек, за исключением
4) «Отражение». Отразим точку
5) Далее смотрим, насколько нам удалось уменьшить функцию, ищем место · Если
и значение функции o Если o Если · Если · Если · Если 6) «Сжатие». Строим точку
и вычисляем в ней значение 7) Если 8) Если 9) Последний шаг – проверка сходимости. Может выполняться по-разному, например, оценкой дисперсии набора точек. Суть проверки заключается в том, чтобы проверить взаимную близость полученных вершин симплекса, что предполагает и близость их к искомому минимуму. Если требуемая точность ещё не достигнута, можно продолжить итерации с шага 2.
Блок – схема метода переменного многогранника Нелдера-Мида.
Блок-схема вышеописанного алгоритма метода Нелдера-Мида выглядит следующим образом:
Рисунок 3 – Блок-схема алгоритма метода Нелдера-Мида.
Тестовая функция.
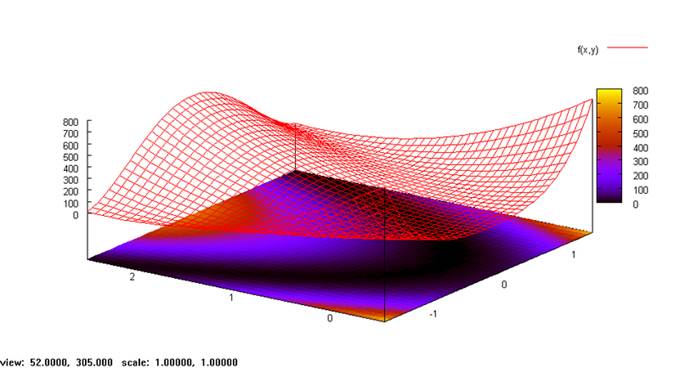
В качестве тестовой функции для метода Нелдера-Мида, была использована функция Розенброка. Это невыпуклая функция, используемая для оценки производительности алгоритмов оптимизации, предложенная Ховардом Розенброком в 1960 году. Считается, что поиск глобального минимума для данной функции является нетривиальной задачей. Является примером тестовой функции для локальных методов оптимизации. Функция Розенброка для двух переменных определяется как:
Она имеет глобальный минимум в точке
Рисунок 4 - Значение функции Розенброка для двух переменных в окрестности точки (x,y) = (0,0).
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2019-11-02; просмотров: 325; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.161.43 (0.005 с.) |

 точка
точка  , образующие симплекс n-мерного пространства. В этих точках вычисляются значения функции:
, образующие симплекс n-мерного пространства. В этих точках вычисляются значения функции: 
 :
:  c наибольшим (из выбранных) значением функции f h {\displaystyle f_{h}}
c наибольшим (из выбранных) значением функции f h {\displaystyle f_{h}}  ,
,  x g {\displaystyle x_{g}} со следующим по величине значением f g {\displaystyle f_{g}}
x g {\displaystyle x_{g}} со следующим по величине значением f g {\displaystyle f_{g}}  и
и  x l {\displaystyle x_{l}} с наименьшим значением функции f l {\displaystyle f_{l}}
x l {\displaystyle x_{l}} с наименьшим значением функции f l {\displaystyle f_{l}}  . Целью дальнейших манипуляций будет уменьшение по крайней мере f h {\displaystyle f_{h}}
. Целью дальнейших манипуляций будет уменьшение по крайней мере f h {\displaystyle f_{h}} 
 не обязательно.
не обязательно. с коэффициентом α (при α=1 это будет центральная симметрия, в общем случае – гомотетия), получим точку
с коэффициентом α (при α=1 это будет центральная симметрия, в общем случае – гомотетия), получим точку  и вычислим в ней функцию:
и вычислим в ней функцию:  . Координаты новой точки вычисляются по формуле:
. Координаты новой точки вычисляются по формуле:
 f r {\displaystyle f_{r}} в ряду f h, f g, f l {\displaystyle f_{h},f_{g},f_{l}}
f r {\displaystyle f_{r}} в ряду f h, f g, f l {\displaystyle f_{h},f_{g},f_{l}}  .
. , то направление выбрано удачное и можно попробовать увеличить шаг. Производим «растяжение». Новая точка
, то направление выбрано удачное и можно попробовать увеличить шаг. Производим «растяжение». Новая точка
 .
. , то можно расширить симплекс до этой точки: присваиваем точке
, то можно расширить симплекс до этой точки: присваиваем точке  и заканчиваем итерацию (переход к шагу 9).
и заканчиваем итерацию (переход к шагу 9).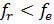 , то переместились слишком далеко: присваиваем точке
, то переместились слишком далеко: присваиваем точке  , то выбор точки неплохой (новая лучше двух прежних). Присваиваем точке
, то выбор точки неплохой (новая лучше двух прежних). Присваиваем точке  , то меняем местами значения
, то меняем местами значения  . Также нужно поменять местами значения
. Также нужно поменять местами значения 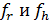 .Переход к шагу 6.
.Переход к шагу 6. , то переход к шагу 6.
, то переход к шагу 6.
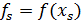 .
. , то присваиваем точке
, то присваиваем точке  и переходим к шагу 9.
и переходим к шагу 9. , то первоначальные точки оказались самыми удачными. Делаем «глобальное сжатие» симплекса – гомотетию к точке с наименьшим значением
, то первоначальные точки оказались самыми удачными. Делаем «глобальное сжатие» симплекса – гомотетию к точке с наименьшим значением 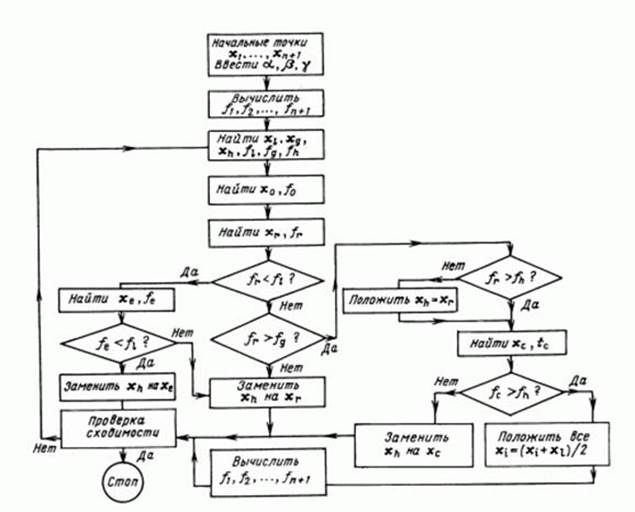

 , где
, где  .
.