Постановка задачи нелинейного программирования

Введение

 

Решение широкого круга задач автоматизированного проектирования и управления связано с поиском оптимальных вариантов, что требует использования соответствующих процедур оптимизации. Оптимизация связана с определением в соответствии с установленными критериями наилучшего (оптимального) решения из множества допустимых вариантов. Методы оптимизации имеют широкий круг практических приложений. В настоящее время разработано множество численных методов для задач как безусловной, так и условной оптимизации. Естественным является стремление выбрать для решения конкретной задачи наилучший метод, позволяющий за наименьшее время использования ЭВМ получить решение с заданной точностью.

Качество численного метода характеризуется многими факторами: скоростью сходимости, временем выполнения одной итерации, объемом памяти ЭВМ, необходимым для реализации метода, классом решаемых задач и т. д. Решаемые задачи также весьма разнообразны: они могут иметь высокую и малую размерность, быть унимодальными (обладающими одним экстремумом) и многоэкстремальными и т. д. Один и тот же метод, эффективный для решения задач одного типа, может оказаться совершенно неприемлемым для задач другого типа. Очевидно, что разумное сочетание разнообразных методов, учет их свойств позволят с наибольшей эффективностью решать поставленные задачи.

В качестве объектов оптимизации могут рассматриваться технические, социально-экономические, производственные, организационные, информационно-телекоммуникационные системы, технологические процессы, транспортные и вычислительные сети, информационные потоки, маршруты и. т. д. При этом структурная оптимизация связана с определением оптимальной структуры объекта. При параметрической оптимизации определяются значения параметров объекта заданной структуры, при которых достигается наилучшее сочетание его свойств.

Целью курсовой работы является изучение методов нелинейной оптимизации, в частности решение задач нелинейной оптимизации методом нулевого порядка – методом переменного многогранника Нелдера-Мида, а также получение практических навыков их программной реализации при проектировании информационных систем. Она заключается в построении математических оптимизационных моделей и разработке алгоритмического и программного обеспечения для решения задач методом переменного многогранника Нелдера-Мида

Выполнение курсовой работы предполагает постановку следующих целей и задач:

§ Формирование постановки задачи нелинейного программирования (ЗНП);

§ Сравнение основных методов решения задач оптимизации данного класса;

§ Углубленное изучение метода Нелдера-Мида поиска оптимального решения и рассмотрение алгоритма его работы;

§ Разработка программного продукта, реализующего рассмотренный алгоритм работы данного метода;

§ Получение в процессе разработки практических навыков программной реализации изученного алгоритма.

 

Теоретическая часть

Блок – схема метода переменного многогранника Нелдера-Мида.

 

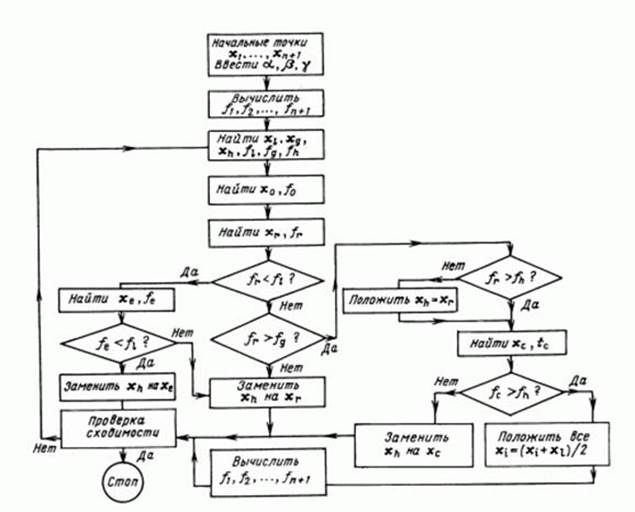
Блок-схема вышеописанного алгоритма метода Нелдера-Мида выглядит следующим образом:

 

Рисунок 3 – Блок-схема алгоритма метода Нелдера-Мида.

 

Тестовая функция.

 

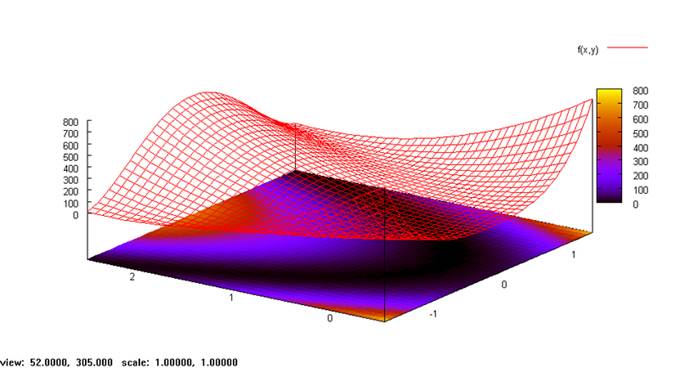
       В качестве тестовой функции для метода Нелдера-Мида, была использована функция Розенброка. Это невыпуклая функция, используемая для оценки производительности алгоритмов оптимизации, предложенная Ховардом Розенброком в 1960 году. Считается, что поиск глобального минимума для данной функции является нетривиальной задачей. Является примером тестовой функции для локальных методов оптимизации.

    Функция Розенброка для двух переменных определяется как:

 

(2.5)

 

Она имеет глобальный минимум в точке , где .

Рисунок 4 - Значение функции Розенброка для двух переменных в окрестности точки (x,y) = (0,0).

 

 

Руководство пользователя

 

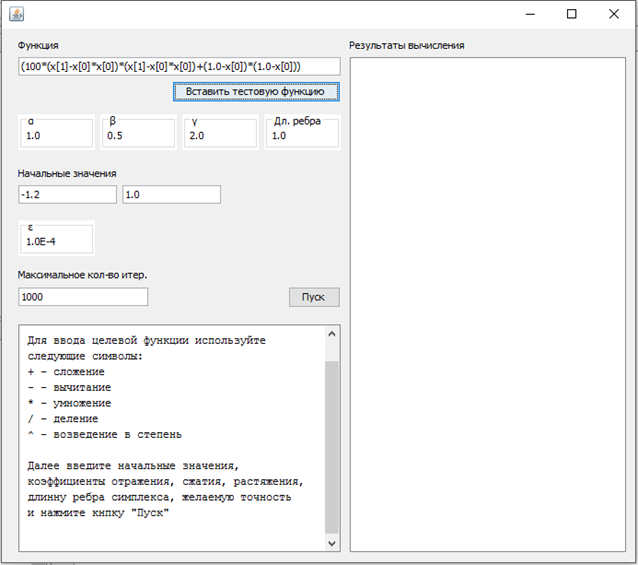
При запуске программы отображается главное окно (Рисунок 5), в котором происходит ввод исходных данных и последующее отображение решения задачи.

 

Рисунок 5 – Главное окно программы.

 

Если работа с программой вызывает затруднения, обратите внимание на справку в нижней части окна.

Далее вводятся значения в поля ввода. Сначала вводится выражение для целевой функции, потом параметры симплекса, начальные значения (начальная точка), точность и максимальное количество итераций. На рисунке 6 показана программа с заполненными полями ввода:

Рисунок 6 – Пример заполнения полей ввода.

 

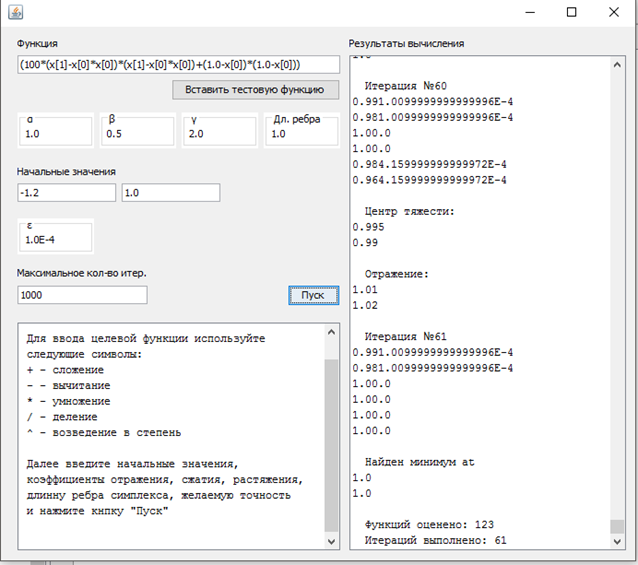
Следующим после заполнения полей ввода действием является нажатие кнопки “Пуск” программы. Сразу после этого в поле вывода, расположенном в правой части окна, будет представлено решение задачи (Рисунок 7):

 

Рисунок 7 – Вывод программой решения задачи.

 

Заключение

 

В результате выполнения данной курсовой работы были изучены основные методы покоординатной оптимизации в задачах нелинейного программирования, в частности, подробному изучению подлежал метод переменного многогранника Нелдера-Мида или метод деформируемого многогранника Нелдера-Мида.

Трудно переоценить важность задач нелинейного программирования для современной экономики и промышленности.

Симплекс-метод Нелдера-Мида является очень эффективным алгоритмом поиска экстремума функции многих переменных, не накладывающим ограничений на гладкость функции. На каждой итерации алгоритма производится как правило одно-два вычисления значений функции, что чрезвычайно эффективно если эти вычисления очень медленны. Кроме того, алгоритма очень прост в реализации. Главным же его недостатком является отсутствие теории сходимости и наличие примеров, когда метод расходится даже на гладких функциях.

Разработанное по заданию программное средство, имеющее в своей основе алгоритм метода Нелдера-Мида, позволяет автоматизировано решать задачи нелинейного программирования и предоставлять результат в удобном для пользователя виде с использованием графического интерфейса.

Непосредственные результаты исследований по данной теме курсовой работы выглядят следующим образом:

§ Сформирована постановки задачи нелинейного программирования (ЗНП) и изучена математическая модель;

§ Проведен сравнительный обзор методов покоординатной оптимизации, позволяющих решать данный класс задач оптимизации;

§ Рассмотрен алгоритм работы метода Нелдера-Мида;

§ Разработан программный продукт, позволяющий автоматизировано решать ЗНП;

§ В процессе разработки получены теоретические и практические навыки использования изученного алгоритма.

 

Список используемой литературы:

 

1. Белецкая С.Ю. Технология автоматизированного решения задач оптимизации: учеб. пособие / С.Ю. Белецкая. – Воронеж: ВГТУ, 2009. – 179 с.

2. Белецкая С.Ю. Математические методы поиска оптимальных решений: учеб.пособие / С.Ю. Белецкая. – Воронеж: ВГТУ, 2006. – 200 с.

3. Батищев Д.И., Львович Я.Е., Фролов В.Н. Оптимизация в САПР / Д.И. Батищев, Я.Е. Львович, В.Н. Фролов. – Воронеж: ВГТУ, 1997. – 416 с.

4. Банди Б. Основы линейного программирования / Б. Банди. – М.: Радио и связь, 1989. – 86 с.

5. Пантелеев А.В. Методы оптимизации в примерах и задачах: учеб.пособие / А.В. Пантелеев, Т.А. Летова. – М.: Высш. шк., 2002. – 544 с.

6. Галеев Э.М. Оптимизация: Теория, примеры, задачи. – М.: Либрком, 2010. – 336 с.

7. Гончаров. В.А. Методы оптимизации: учеб.пособие / А.В. Гончаров. – М.: Высшее образование, 2009. – 191 с.

8. Васильев Ф.П. Методы оптимизации. – М.: Факториал пресс, 2002. – 824 с.

9. Шилд Г. Java 8. Полное руководство – 9-е изд. – CПб.: Издательский дом "Вильяме", 2015. – 1 376 с.

 

 

ПРИЛОЖЕНИЕ A

(обязательное)

 

Form1.cs

 

using System;

using System.Collections.Generic;

using System.ComponentModel;

using System.Data;

using System.Drawing;

using System.Linq;

using System.Text;

using System.Threading.Tasks;

using System.Windows.Forms;

using info.lundin.math;

 

namespace Method_Hook_Jeeves

{

public partial class MainForm: Form

{

   string ogran;

   double f; // функция f(x1,x2)

   double x1, x2, xt1, xt2; // точки

   double vpx1, vpx2; // вектор приращения

   double step; // коэффициент уменьшения шага

   double acc; // точность

   string func; // строка для сохранения функции

   Boolean flag; //флаг проверки

   double[] fun; //массив хранящий значения функций

   int count; //счетчик

   Boolean xflag; //переменная отражает успех или неудачу исследующего поиска x1,x2

   double f_old; // переменная нужна для сравнения новой функции

   double fkm1; // значение предыдущей функции

   Boolean iflag; // флаг отражает был ли весь поиск успешным или нет

   double[] mainx1, mainx2; //массивы хранящие базовые точки

   double kp1, kp2, kp1_old, kp2_old; // точки, построенные при движении по образцу

 

   private void button2_Click(object sender, EventArgs e)

   {

       this.Width = 652;

   }

 

   private void button1_Click(object sender, EventArgs e)

   {

       this.Width = 387;

   }

 

   double ftest,x1test,x2test; // функция для проверки поля

   int proverka; // счетчик для предотвращения зацикливания

 

   public MainForm()

   {

       InitializeComponent();

   }

 

   private void calculation_Click(object sender, EventArgs e)

   {

       // параметры формы

       try

       {

           x1 = Convert.ToDouble(textBox2.Text);

           x2 = Convert.ToDouble(textBox3.Text);

           func = textBox1.Text;

           vpx1 = Convert.ToDouble(textBox5.Text);

           vpx2 = Convert.ToDouble(textBox4.Text);

           step = Convert.ToDouble(textBox6.Text);

           ogran = textBox9.Text;

           fun = new double[1000];

           mainx1 = new double[1000];

           mainx2 = new double[1000];

           flag = true;

           if (step <= 1)

           {

               MessageBox.Show("Шаг должен быть > 1", "Неверные данные", MessageBoxButtons.OK, MessageBoxIcon.Warning);

               flag = false;

           }

           acc = Convert.ToDouble(textBox7.Text);

           if (acc >= 1 || acc < 0)

           {

               MessageBox.Show("Точность должна быть <1 и >0", "Неверные данные", MessageBoxButtons.OK, MessageBoxIcon.Warning);

               flag = false;

 

           }

           try

           {

               x1test = x1;

               x2test = x2;

               ExpressionParser parser = new ExpressionParser();

               parser.Values.Add("x1", x1test);

               parser.Values.Add("x2", x2test);

               ftest = parser.Parse(textBox1.Text);

           }

           catch

           {

               MessageBox.Show("Возникла ошибка при вычислении функции", "Неверные данные", MessageBoxButtons.OK, MessageBoxIcon.Warning);

               flag = false;

           }

           if (flag == true) start();

 

       }

       catch (FormatException)

       {

           MessageBox.Show("Введены некорректные данные в поля параметров", "Неверные данные", MessageBoxButtons.OK, MessageBoxIcon.Warning);

       }

          

   }

 

   public double regexpr(double x, double y)

   {

       ExpressionParser parser = new ExpressionParser();

       parser.Values.Add("x1", x);

       parser.Values.Add("x2", y);

       return parser.Parse(textBox1.Text);

 

   }

 

   public Boolean uspex(double a, double b)

   {

       if (a < b)

           return true;

       else

           return false;

   }

 

   public void ipoisk(double xodin, double xdva, int p)

   {

       f = regexpr(xodin, xdva);

       xflag = uspex(f, f_old);

       if (p == 0)

           textBox8.AppendText("Фиксируя переменную x" + (p + 1) + "=" + xdva + ", дадим приращение x" + Environment.NewLine);

       else

           textBox8.AppendText("Фиксируя переменную x" + (p + 1) + "=" + xodin + ", дадим приращение x" + Environment.NewLine);

       textBox8.AppendText("f(" + xodin + "," + xdva + ")= " + f + " < " + f_old + "? " + xflag + Environment.NewLine);

       if (xflag == true)

       {

           if (p == 0)

               x1 = xt1;

           else

               x2 = xt2;

          // f_old = f;

           iflag = true;

       }

           

   }

 

 

   public void start()

   {

       // Шаг 1. Инициализация

       count = 0;

       fun[count] = regexpr(x1, x2);

       textBox8.AppendText("Вычислим значение функции в т. (" + x1 + "," + x2 + "). f=" + fun[count] + Environment.NewLine);

       mainx1[0] = x1;

       mainx2[0] = x2;

       textBox8.AppendText("-----------------------------------------------------------------------------" + Environment.NewLine);

       proverka = 1;

       f_old = fun[count];

       // Шаг 2. Исследующий поиск

       shag2:

       textBox8.AppendText("Исследующий поиск: " + Environment.NewLine);

       iflag = false;

       proverka = proverka + 1;

       // исследующий поиск x1

       xt1 = x1 + vpx1;

       ipoisk(xt1, x2, 0);

       // исследующий поиск x2

       xt2 = x2 + vpx2;

       ipoisk(x1, xt2, 1);

       if (iflag == false)

       { // исследующий поиск x1 в противоположном направлении

           xt1 = x1 - vpx1;

           ipoisk(xt1, x2, 0);

           // исследующий поиск x2 в противоположном направлении

           xt2 = x2 - vpx2;

           ipoisk(x1, xt2, 1);

       }

       // Шаг 3. Проверка успеха исследующего поиска

       if (iflag == true)

           goto predshag5;

       else

           goto shag4;

       predshag5:

           count = count + 1;

           mainx1[count] = x1;

           mainx2[count] = x2;

           fun[count] = regexpr(mainx1[count], mainx2[count]);

           textBox8.AppendText("x" + count + "=(" + x1 + "," + x2 + ")=" + fun[count] + Environment.NewLine);

           textBox8.AppendText("-----------------------------------------------------------------------------" + Environment.NewLine);

       // Шаг 5. Поиск по образцу

           kp1_old = mainx1[count-1];

           kp2_old = mainx2[count-1];

       shag5:

           kp1 = mainx1[count] + (mainx1[count] - kp1_old);

           kp2 = mainx2[count] + (mainx2[count] - kp2_old);

           f = regexpr(kp1, kp2);

           proverka = proverka + 1;

           if (proverka > 100)

               goto konec2;  

           

           /*if (f >= fun[count])

             {

               kp1 = kp1_old;

               kp2 = kp2_old;

               f = regexpr(kp1, kp2);

           }*/

 

           textBox8.AppendText("Поиск по образцу:" + Environment.NewLine);

           textBox8.AppendText("p(" + kp1 + "," + kp2 + ")=" + f + Environment.NewLine);

               

           // Шаг 6. Исследующий поиск после поиска по образцу

           textBox8.AppendText("Исследующий поиск после поиска по образцу: " + Environment.NewLine);

           f_old = f;

           iflag = false;

           x1 = kp1;

           x2 = kp2;

           // исследующий поиск x1

           xt1 = x1 + vpx1;

           ipoisk(xt1, x2, 0);

           // исследующий поиск x2

           xt2 = x2 + vpx2;

           ipoisk(x1, xt2, 1);

           if (iflag == false)

           { // исследующий поиск x1 в противоположном направлении

               xt1 = x1 - vpx1;

               ipoisk(xt1, x2, 0);

               // исследующий поиск x2 в противоположном направлении

               xt2 = x2 - vpx2;

               ipoisk(x1, xt2, 1);

           }

           if (iflag == false) goto shag4;

           textBox8.AppendText("f^k+1 = " + f + Environment.NewLine);

           textBox8.AppendText("f^k = " + fun[count] + Environment.NewLine);

               

           // Шаг 7. Выполняется ли неравенство f(x^(k+1))<f(x^k)?

           

           if (f < fun[count])

           {

               kp1_old = kp1;

               kp2_old = kp2;

               fkm1 = regexpr(kp1, kp2);

               count++;

               mainx1[count] = x1;

               mainx2[count] = x2;

               fun[count] = regexpr(mainx1[count], mainx2[count]);

               textBox8.AppendText("x^k-1(" + kp1_old + "," + kp2_old + ")=" + fkm1 + Environment.NewLine);

               textBox8.AppendText("---- x" + count + "=(" + x1 + "," + x2 + ")=" + fun[count] + "----" + Environment.NewLine);

               textBox8.AppendText("-----------------------------------------------------------------------------" + Environment.NewLine);

               goto shag5;

           }

           else

           {

               x1 = mainx1[count];

               x2 = mainx2[count];

               goto shag4;

           }

   // Шаг 4. Проверка на окончание поиска

       shag4:

           

       if (Math.Sqrt(vpx1*vpx1+vpx2*vpx2) <= acc)

       {

 

           textBox8.AppendText("Неравенство выполняется: " + Math.Sqrt(vpx1 * vpx1 + vpx2 * vpx2) + "<=" + acc + Environment.NewLine);

           goto konec;

       }

       else

       {

           vpx1 = vpx1 / step;

           vpx2 = vpx2 / step;

           textBox8.AppendText("dX1=" + vpx1 + " dX2=" + vpx2 + Environment.NewLine);

           goto shag2;

       }

   konec:

       textBox8.AppendText("Ответ: x(" + kp1 + ";" + kp2 + "),f(x)=" + f_old);

   konec2:

       textBox8.AppendText("Верное решение найдено");

 

   }

}

}

Введение

 

Решение широкого круга задач автоматизированного проектирования и управления связано с поиском оптимальных вариантов, что требует использования соответствующих процедур оптимизации. Оптимизация связана с определением в соответствии с установленными критериями наилучшего (оптимального) решения из множества допустимых вариантов. Методы оптимизации имеют широкий круг практических приложений. В настоящее время разработано множество численных методов для задач как безусловной, так и условной оптимизации. Естественным является стремление выбрать для решения конкретной задачи наилучший метод, позволяющий за наименьшее время использования ЭВМ получить решение с заданной точностью.

Качество численного метода характеризуется многими факторами: скоростью сходимости, временем выполнения одной итерации, объемом памяти ЭВМ, необходимым для реализации метода, классом решаемых задач и т. д. Решаемые задачи также весьма разнообразны: они могут иметь высокую и малую размерность, быть унимодальными (обладающими одним экстремумом) и многоэкстремальными и т. д. Один и тот же метод, эффективный для решения задач одного типа, может оказаться совершенно неприемлемым для задач другого типа. Очевидно, что разумное сочетание разнообразных методов, учет их свойств позволят с наибольшей эффективностью решать поставленные задачи.

В качестве объектов оптимизации могут рассматриваться технические, социально-экономические, производственные, организационные, информационно-телекоммуникационные системы, технологические процессы, транспортные и вычислительные сети, информационные потоки, маршруты и. т. д. При этом структурная оптимизация связана с определением оптимальной структуры объекта. При параметрической оптимизации определяются значения параметров объекта заданной структуры, при которых достигается наилучшее сочетание его свойств.

Целью курсовой работы является изучение методов нелинейной оптимизации, в частности решение задач нелинейной оптимизации методом нулевого порядка – методом переменного многогранника Нелдера-Мида, а также получение практических навыков их программной реализации при проектировании информационных систем. Она заключается в построении математических оптимизационных моделей и разработке алгоритмического и программного обеспечения для решения задач методом переменного многогранника Нелдера-Мида

Выполнение курсовой работы предполагает постановку следующих целей и задач:

§ Формирование постановки задачи нелинейного программирования (ЗНП);

§ Сравнение основных методов решения задач оптимизации данного класса;

§ Углубленное изучение метода Нелдера-Мида поиска оптимального решения и рассмотрение алгоритма его работы;

§ Разработка программного продукта, реализующего рассмотренный алгоритм работы данного метода;

§ Получение в процессе разработки практических навыков программной реализации изученного алгоритма.

 

Теоретическая часть

Постановка задачи нелинейного программирования

 

Задачи нелинейной оптимизации заключаются в определении оптимального (максимального или минимального) значения нелинейной целевой функции многих переменных, когда на переменные имеются ограничения равенств или неравенств. Также, задачи нелинейной оптимизации называются еще задачами нелинейного программирования (задачами НП).

В общем виде задача нелинейной оптимизации может быть сформулирована следующим образом:

 

(1.1)

 

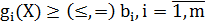
где хотя бы одна из функций f(x), g(x) является нелинейной. Здесь  – вектор варьируемых параметров. На переменные  также могут накладываться ограничения: , где  и - нижняя и верхняя границы для каждой j-й переменной. Задача без ограничений называется задачей безусловнойопти­мизации, задача с ограничениями - задачей условной оптимизации.