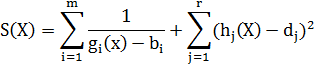Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы решения задач нелинейной оптимизацииСодержание книги
Поиск на нашем сайте
1.2.1. Преобразование задач с ограничениями к задачам безусловной оптимизации
Одним из наиболее распространенных и часто используемых на практике приемов решения задач нелинейной оптимизации с ограничениями является их преобразование к задачам безусловной оптимизации. При этом для учета прямых и функциональных ограничений могут быть использованы различные подходы. Рассмотрим задачу нелинейной оптимизации с прямыми и функциональными ограничениями:
Прямые ограничения на варьируемые параметры можно исключить из данной задачи с помощью замены переменных:
где Тогда целевая функция задачи может быть переформулирована следующим образом:
Аналогичным образом переформулируются и функциональные ограничения:
Переформулированная в новых переменных задача примет вид:
При этом прямые ограничения из задачи исключаются, так как новые переменные
Существует большое количество стандартных функций замены переменных, использующихся для учета прямых ограничений различных видов. Некоторые виды ограничений на варьируемые параметры и функции преобразования, позволяющие исключить их из задач оптимизации, представлены в таблице 1:
Таблица 1 – Типы ограничений и функций преобразования.
Рассмотрим основные подходы к учету функциональных ограничений. Пусть решается задача минимизации целевой функции f(X) с функциональными ограничениями, представленными в виде системы неравенств (1.8) и равенств (1.9):
Для учета функциональных ограничений обычно используется метод штрафных функций. При этом осуществляется переход от исходной целевой функции f(X) к следующей функции:
Здесь S(X) — штрафная функция (функция штрафа), отличная нуля вне допустимой области D; В результате решение задач с ограничениями сводится к решению последовательности задач безусловной оптимизации вспомогательной функции Р(Х). При этом штрафная функция S(X) формируется таким образом, чтобы при нарушении ограничений задачи изводился некоторый “штраф” за их нарушение. При решении задачи минимизации “штраф” заключается в том, что к целевой функции прибавляется некоторое положительное число, “отбрасывая” тем самым оптимизационный процесс от оптимальной точки. Существует два метода построения штрафных функций: · метод внутренних штрафных функций (барьерных функций); · метод внешних штрафных функций. Метод внутренних штрафных функций предназначен для учета только ограничений - неравенств и характеризуется следующей основной функцией штрафа:
При этом предполагается, что ограничения-равенства (1.9) в задаче отсутствуют. Тогда целевая функция оптимизационной задачи примет вид:
При этом параметр При использовании внутренних штрафных функций поиск минимума следует начинать с внутренней точки допустимой области, то есть с точки, в которой все ограничения выполнены как неравенства. При выходе на границу допустимой области значение штрафной функции S(X) (штраф) будет бесконечным, следовательно, оптимизационный процесс никогда не выйдет за прсделы допустимой области. Недостатком данного метода является то, что он не позволяет решать задачи с ограничениями-равенствами. Кроме того, для их использования необходимо знать начальную допустимую точку. В этой связи более целесообразным является использование внешних штрафных функций. С помощью метода внешних штрафных функций учитываются как ограничения-неравенства
При этом если ограничения не нарушаются, то есть Может быть использована также комбинированная штрафная функция, в которой ограничения-неравенства учитываются с помощью внешних штрафных функций, а ограничения - равенства с помощью внутренних (барьерных) функций.
Таким образом, задачи с ограничениями с помощью замены переменных и методов штрафных функций могут быть преобразованы к задачам безусловной оптимизации. После соответствующих преобразований полученные задачи решаются с использованием методов безусловной оптимизации.
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-11-02; просмотров: 162; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.57.57 (0.005 с.) |

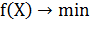
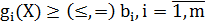
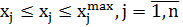
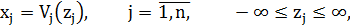
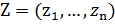 – вектор новых варьируемых параметров.
– вектор новых варьируемых параметров.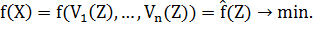
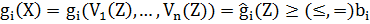
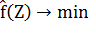
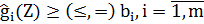
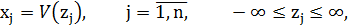
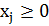
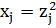
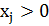
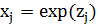
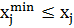
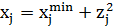
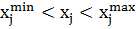
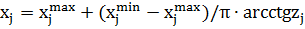
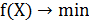
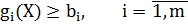
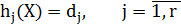
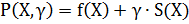
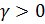 - коэффициент штрафа, значение которого может быть постоянным или меняться на различных итерациях. Во втором случае параметр
- коэффициент штрафа, значение которого может быть постоянным или меняться на различных итерациях. Во втором случае параметр 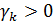 настраивается в ходе оптимизационного процесса (k - номер итерации).
настраивается в ходе оптимизационного процесса (k - номер итерации).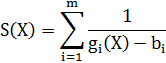
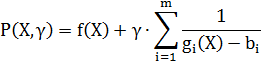
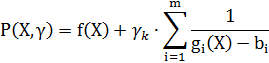
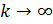 (k - номер итерации).
(k - номер итерации).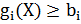 , так и ограничения-равенства
, так и ограничения-равенства 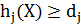 . Наибольшее распространение получили штрафные функции следующего вида:
. Наибольшее распространение получили штрафные функции следующего вида: