
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы покоординатной оптимизацииСодержание книги Поиск на нашем сайте
В методах покоординатной оптимизации в качестве направлений поиска выбираются координатные оси пространства варьируемых параметров. При этом на каждой k-й итерации выполняется n шагов циклического покоординатного спуска из текущей точки
где
Таким образом, в координатной форме шаги циклического спуска имеют следующий вид:
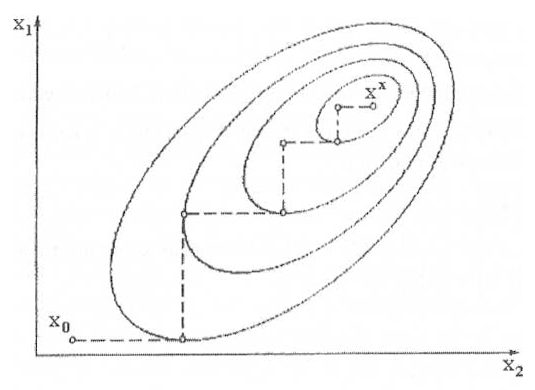
Геометрической интерпретацией траектории покоординатного поиска является ломаная, состоящая из отрезков, параллельных осям координат (рисунок 1). На рисунке 1 изображены также линии уровня целевой функции двух переменных. Каждая линия уровня соответствует некоторому постоянному значению целевой функции Необходимо заметить, что для нелинейной целевой функции линии уровня часто имеют овражный характер. При этом целевая функция сильно меняется по одним направлениям и слабо - по другим. Такие овражные ситуации создают значительные трудности для оптимизации.
Рисунок 1 – Интерпретация траектории покоординатного поиска.
К простейшим алгоритмам покоординатной оптимизации можно отнести алгоритм покоординатного спуска с постоянным шагом и релаксационный метод Гаусса-Зейделя. Различия между этими двумя алгоритмами заключается в способе выбора шага поиска a. Покоординатный спуск с постоянным шагом. В этом методе на каждой k-й итерации циклический покоординатный спуск заключается в следующем. Сначала осуществляется движение из точки
Если это приводит к уменьшению значения целевой функции:
В случае уменьшения значения целевой функции осуществляется переход в точку b. Релаксационный алгоритм Гаусса-Зейделя Отличие данного алгоритма от предыдущего заключается в том, что в нем на каждой k-й итерации определяются оптимальные длины шагов · Задается начальное приближение вычислений ε > 0. При этом k=0, · Осуществляется циклический покоординатный спуск из точки
В результате каждого i-го шага внутреннего цикла определяется очередная координата · Проверяется выполнение критерия окончания итерационного процесса. Если c. Дальнейшим развитием методов покоординатной оптимизации является метод конфигураций Хука-Дживса. В данном методе этап циклического покоординатного поиска вдоль координатных осей чередуется с этапом экстраполяции, т.е. движения в направлении, соединяющем две перспективные точки На этапе исследующего поиска из базисной точки
Рисунок 2 – Шаги метода Хука - Дживса.
Если этап исследующего поиска оказывается успешным, т.е. Недостатком описанных выше методов покоординатной оптимизации является то, что при минимизации функций f(X), имеющих овраг, дно которого не ориентировано вдоль одной из координатных осей, процесс поиска сильно замедляется и может вообще остановиться вдали от точки локального минимума.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-11-02; просмотров: 585; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.175.191 (0.006 с.) |

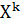 вдоль каждой из n координатных осей. Покоординатный спуск сводится к поочередному изменению переменных вдоль одной из осей:
вдоль каждой из n координатных осей. Покоординатный спуск сводится к поочередному изменению переменных вдоль одной из осей:
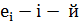 координатный n – мерный векторб у которого i – й элемент равен 1, а остальные элементы равны 0:
координатный n – мерный векторб у которого i – й элемент равен 1, а остальные элементы равны 0: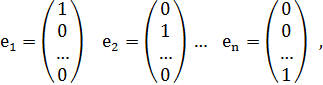
 – длина шага поиска по i – й переменной на k – ой итерации.
– длина шага поиска по i – й переменной на k – ой итерации.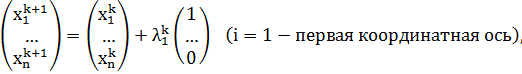

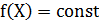 (в случае большего числа переменных речь идет о поверхностях уровня целевой функции). Таким образом, процесс минимизации заключается в последовательном переходе от одной линии уровня
(в случае большего числа переменных речь идет о поверхностях уровня целевой функции). Таким образом, процесс минимизации заключается в последовательном переходе от одной линии уровня 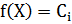 к линии уровня с меньшим значением целевой функции
к линии уровня с меньшим значением целевой функции 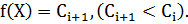
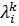 .
.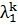 вдоль 1-й координатной оси:
вдоль 1-й координатной оси: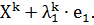
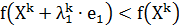 , осуществляется переход в точку
, осуществляется переход в точку 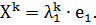 В противном случае производится пробный шаг в противоположном направлении:
В противном случае производится пробный шаг в противоположном направлении: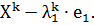
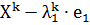 , в противном случае переход в новую точку не производится. Затем рассматривается следующая координатная ось. Аналогичные действия повторяются для всех координатных осей. Если в результате движения вдоль всех координатных осей значение целевой функции не уменьшилось, осуществляется дробление шага, и циклический покоординатный спуск повторяется из точки
, в противном случае переход в новую точку не производится. Затем рассматривается следующая координатная ось. Аналогичные действия повторяются для всех координатных осей. Если в результате движения вдоль всех координатных осей значение целевой функции не уменьшилось, осуществляется дробление шага, и циклический покоординатный спуск повторяется из точки 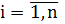 в результате решения вспомогательных задач одномерной оптимизации. При этом процедура поиска точки минимума
в результате решения вспомогательных задач одномерной оптимизации. При этом процедура поиска точки минимума 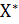 сводится к следующей последовательности действий.
сводится к следующей последовательности действий.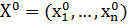 и точность
и точность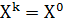 .
. , i = l...n с выбором оптимальной длины поискового шага
, i = l...n с выбором оптимальной длины поискового шага 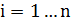 . Эта процедура образует внутренний цикл, в процессе которого осуществляется одномерная минимизация функции
. Эта процедура образует внутренний цикл, в процессе которого осуществляется одномерная минимизация функции 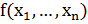 по каждой переменной
по каждой переменной 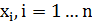 :
: 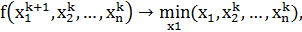
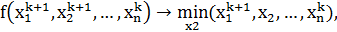
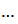

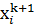 точки
точки 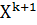 . После окончания внутреннего цикла в качестве нового приближения принимается точка
. После окончания внутреннего цикла в качестве нового приближения принимается точка 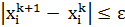 для всех i=1..n, работа алгоритме заканчивается. В противном случае осуществляется переход к шагу 2 (при этом k=k+l).
для всех i=1..n, работа алгоритме заканчивается. В противном случае осуществляется переход к шагу 2 (при этом k=k+l).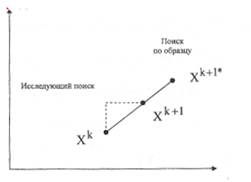
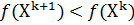 , реализуется этап поиска по образцу. При этом производится движение из точки
, реализуется этап поиска по образцу. При этом производится движение из точки 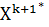 в направлении
в направлении 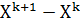 , после чего осуществляется исследующий поиск вокруг полученной точки
, после чего осуществляется исследующий поиск вокруг полученной точки 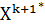 . Если полученное при этом значение целевой функции меньше, чем значение в точке
. Если полученное при этом значение целевой функции меньше, чем значение в точке 


