
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормальный закон на плоскости
Задача 3. Случайная точка а) написать выражение для плотности вероятности системы б) изобразить на плоскости области
в) вычислить вероятность г) вычислить вероятность д) определить, какое минимальное количество опытов нужно произвести для того, чтобы случайная точка оказалась в области Решение. а) Нормальный закон распределения для системы двух случайных величин
где
б) Область
где
Рис 2.5
Область
Рис. 2.6
Следовательно, для вычисления искомой вероятности целесообразно применение формулы
Область
Рис. 2.7
Найдем вероятность попадания в область
Область
Рис. 2.8
Искомую вероятность можно найти, исходя из симметричности поверхности распределения относительно плоскостей
Вероятность попадания случайной точки
где
Рис. 2.9 случайный величина распределение дисперсия
в) Для определения вероятности
Затем находим вероятность того, что случайная точка при трех опытах ни разу не попадет в
и, наконец, искомую вероятность:
г) Вероятность
и вероятности попадания случайной точки в область
Итак, искомая вероятность
д) Если событие в каждом опыте может наступить с вероятностью
По условию,
т.е. необходимо провести как минимум 1 опыта.
|
|||||
|
Последнее изменение этой страницы: 2020-03-14; просмотров: 114; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.86.134 (0.011 с.) |
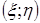 распределена по нормальному закону с параметрами
распределена по нормальному закону с параметрами 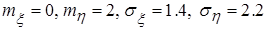 ,
, 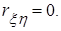 Требуется:
Требуется: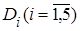 и вычислить вероятности попадания случайной точки
и вычислить вероятности попадания случайной точки 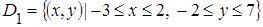 ,
,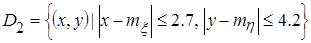 ,
,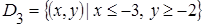 ,
,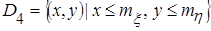 ,
,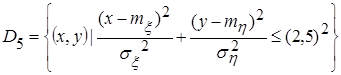 ;
;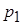 того, что при трех независимых опытах случайная точка попадет хотя бы один раз в область
того, что при трех независимых опытах случайная точка попадет хотя бы один раз в область 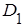 ;
;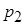 того, что при первых двух опытах случайная точка окажется хотя бы один раз в области
того, что при первых двух опытах случайная точка окажется хотя бы один раз в области 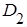 ;
;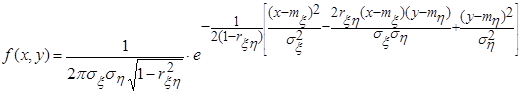 ,
,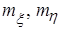 - математические ожидания случайных величин,
- математические ожидания случайных величин, 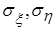 - средние квадратические отклонения,
- средние квадратические отклонения, 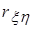 - коэффициент корреляции. Поэтому плотность вероятности данной системы имеет вид
- коэффициент корреляции. Поэтому плотность вероятности данной системы имеет вид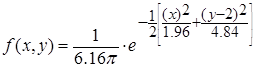 .
.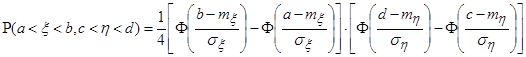 ,
,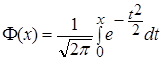 - функция Лапласа, значения которой находятся по таблице, вычисляем вероятность попадания случайной точки
- функция Лапласа, значения которой находятся по таблице, вычисляем вероятность попадания случайной точки 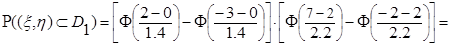
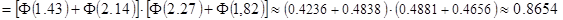
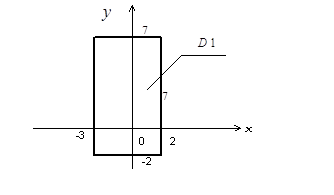
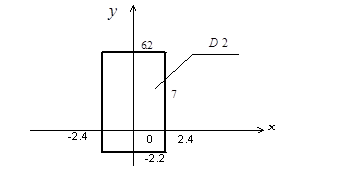
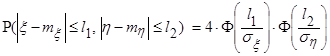
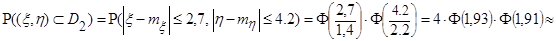
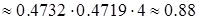
 является квадрантом с вершиной в точке (-3-2) (рис.2.7).
является квадрантом с вершиной в точке (-3-2) (рис.2.7).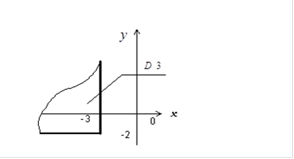
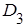 :
: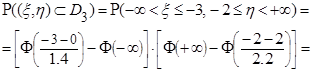
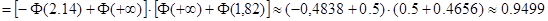 .
.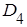 является квадрантом с вершиной в центре рассеивания
является квадрантом с вершиной в центре рассеивания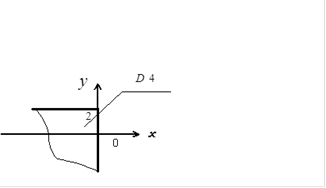
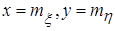 :
: .
.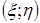 в эллипс рассеивания
в эллипс рассеивания 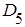 (рис.2.9) вычисляем по соответствующей формуле:
(рис.2.9) вычисляем по соответствующей формуле: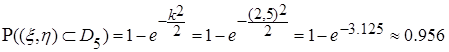 ,
,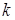 - размеры полуосей эллипса рассеивания в единицах среднего квадратического отклонения по направлению главных осей рассеивания.
- размеры полуосей эллипса рассеивания в единицах среднего квадратического отклонения по направлению главных осей рассеивания.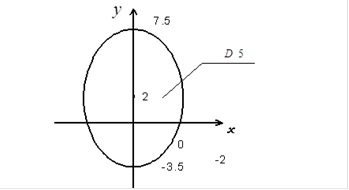
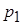 хотя бы одного попадания в область
хотя бы одного попадания в область 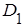 при трех независимых опытах перейдем к противоположному событию, т.е. к тому, что в результате трех опытов случайная точка ни разу не окажется в области
при трех независимых опытах перейдем к противоположному событию, т.е. к тому, что в результате трех опытов случайная точка ни разу не окажется в области 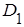 . Вероятность того, что случайная точка в результате опыта не попадет в область
. Вероятность того, что случайная точка в результате опыта не попадет в область 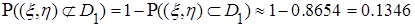
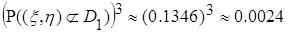
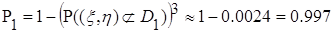
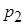 того, что при первых двух опытах случайная точка окажется хотя бы один раз в области
того, что при первых двух опытах случайная точка окажется хотя бы один раз в области 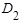 , равна по теореме умножения вероятностей произведению вероятности того, что при двух опытах случайная точка попадет хотя бы раз в область
, равна по теореме умножения вероятностей произведению вероятности того, что при двух опытах случайная точка попадет хотя бы раз в область 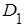 :
: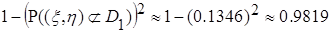
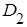 :
: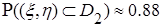 .
.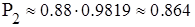 .
.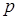 , то количество
, то количество 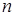 опытов, которые необходимо произвести для того, чтобы с вероятностью
опытов, которые необходимо произвести для того, чтобы с вероятностью 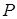 можно было утверждать, что данное событие произойдет хотя бы один раз, находится по формуле
можно было утверждать, что данное событие произойдет хотя бы один раз, находится по формуле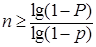 .
.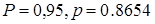 , тогда
, тогда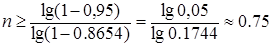 ,
,


