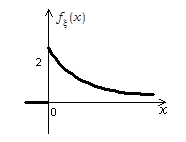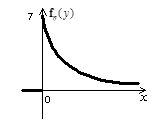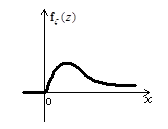Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые характеристики функции двух случайных величин ⇐ ПредыдущаяСтр 4 из 4
Задача 6. Случайная величина x распределена равномерно в интервале (2;4), а независимая от нее случайная величина h распределена по нормальному закону с параметрами а) записать плотности вероятности б) вычислить математическое ожидание и дисперсию случайной величины
в) вычислить математическое ожидание случайной величины
Решение а) Так как случайная величина x имеет равномерное распределение, а h - нормальное распределение, то их плотности вероятности определяются соответственно выражениями:
Следовательно,
б) Запишем числовые характеристики исходных случайных величин:
Используя свойства математического ожидания и дисперсии функции случайных величин, получим:
Итак, искомые числовые характеристики
в) Зная числовые характеристики исходных случайных величин, пользуясь свойствами и определением математического ожидания функции непрерывной случайной величины, имеем:
=
Таким образом,
Числовые характеристики функции трех случайных величин Задача 7. Для системы трех случайных величин (
Требуется: а) вычислить математическое ожидание и дисперсию случайной величины
б) вычислить математическое ожидание случайной величины
Решение Согласно заданной корреляционной матрице имеем:
Искомые числовые характеристики найдем, пользуясь свойствами математического ожидания, дисперсии и корреляционного момента:
а)
Искомые характеристики
б)
=
Таким образом,
Характеристическая функция Задача 8. Для данной плотности вероятности Решение. I способ. Воспользуемся методами операционного исчисления. Так как данная плотность вероятности
II способ. Характеристическую функцию
Вычислим
Композиция законов распределения Задача 9. Независимые случайные величины x и h распределены равномерно на отрезке [2; 4], т.е. их плотности вероятностей имеют вид:
Определить плотность вероятности Решение Воспользуемся аппаратом характеристических функций и методами операционного исчисления. Для этого найдём характеристические функции Найдём для
Следовательно,
Далее, используя свойство запаздывания оригинала и операционное соотношение
Проверим условие нормировки для функции
Графики функций
Рис. 2.13 Рис. 2.14 Рис. 2.15
|
|||||
|
Последнее изменение этой страницы: 2020-03-14; просмотров: 88; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.25.163 (0.015 с.) |
 ,
, 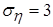 . Требуется:
. Требуется: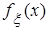 и
и 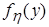 для случайных величин x и h;
для случайных величин x и h;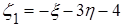 ;
;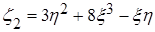 .
.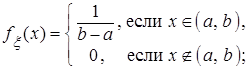
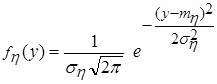
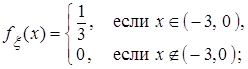
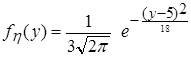
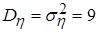 ,
, 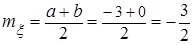 ,
,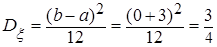
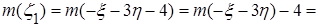
 ;
;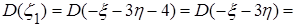
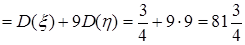
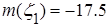 ,
, 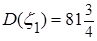 .
.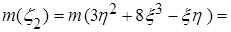
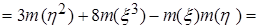
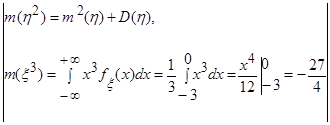 =
= 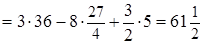 .
.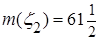 .
.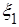 ,
,  ,
, 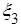 ) даны математические ожидания
) даны математические ожидания 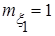 ,
, 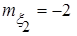 ,
,  и корреляционная матрица
и корреляционная матрица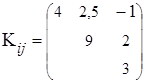
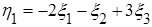 ;
;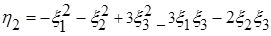 .
.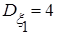 ,
, 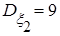 ,
, 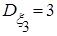 ;
;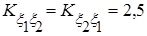 ,
, 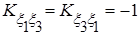 ,
, 
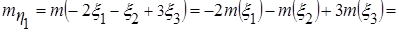
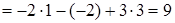 ;
;
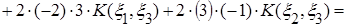
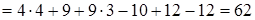 .
.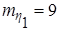 ,
, 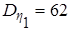 .
.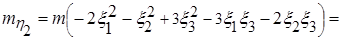
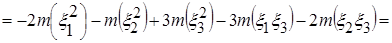
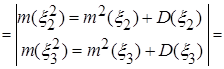
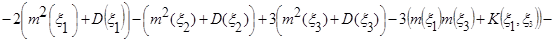
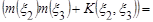
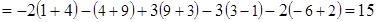 .
.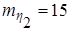
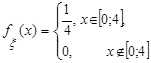 найти характеристическую функцию
найти характеристическую функцию  и с её помощью вычислить математическое ожидание
и с её помощью вычислить математическое ожидание  .
.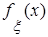 является оригиналом, то характеристическая функция
является оригиналом, то характеристическая функция 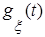 для неё является изображением. Найдём его, учитывая свойство линейности преобразования Лапласа и соотношение
для неё является изображением. Найдём его, учитывая свойство линейности преобразования Лапласа и соотношение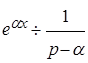 , где
, где 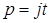

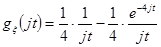
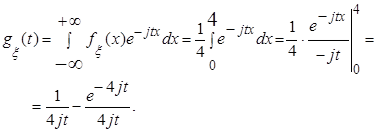
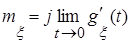 . Имеем:
. Имеем: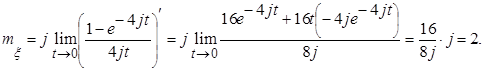
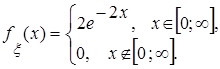
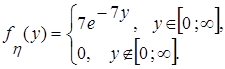
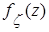 случайной величины
случайной величины 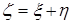 , проверить условие нормировки для
, проверить условие нормировки для 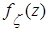 и построить графики функций
и построить графики функций 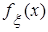 ,
, 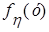 ,
, 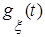 и
и 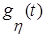 как изображения для плотностей вероятностей
как изображения для плотностей вероятностей 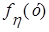 . Далее, учитывая независимость случайных величин x и
. Далее, учитывая независимость случайных величин x и 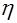 , получим характеристическую функцию как произведение характеристических функций слагаемых случайных величин
, получим характеристическую функцию как произведение характеристических функций слагаемых случайных величин 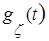 =
=  ∙
∙ 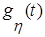 . После этого, совершив обратное преобразование Лапласа, найдём искомую плотность вероятности
. После этого, совершив обратное преобразование Лапласа, найдём искомую плотность вероятности 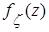 как оригинал для характеристической функции
как оригинал для характеристической функции  .
.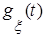 и
и 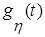 , используя свойства линейности преобразования Лапласа, запаздывания оригинала и операционное соотношение
, используя свойства линейности преобразования Лапласа, запаздывания оригинала и операционное соотношение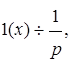 где
где 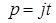 :
: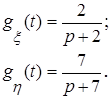
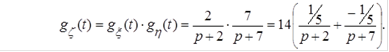
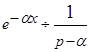 , находим искомую плотность
, находим искомую плотность 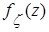 как оригинал для характеристической функции
как оригинал для характеристической функции 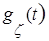
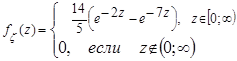
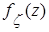 :
: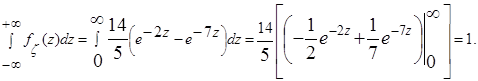
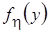 ,
, 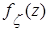 приведены на рис. 2.13 - 2.15:
приведены на рис. 2.13 - 2.15: