
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные тригонометрические тождества.Содержание книги
Поиск на нашем сайте
1. Найдите значение остальных функций, если а) cos α = -0,6; б) sinα = 2. Найдите значение остальных функций, если 0 < α < а) sinα = 0,6; б) cos α = г) sinα = 3. Найдите: а) tg α, если sinα = б) cos α, если ctg α = в) ctg α, если cos α = - в) sinα, если tg α = -1 и 4. Упростите выражение:
5.Упростите выражение
не зависит от значения β.
7.Упростите выражение: а) tg(- α)• cos α + sinα; б) 8. Докажите тождество а) (tgx + ctgx)2 - (tgx - ctgx)2 = 4 б) (2 + sinα)(2 - sinα) + (2 + cos α)(2 - cos α) = 7 в) г)
Формулы приведения Замените тригонометрической функцией угла
2.Найдие значение выражения
3. Упростите выражение
4. Преобразуйте выражение а) sin2( π +α); б) tg2 ( 5. Упростите выражение а) sin(900 – α) + cos(1800 + α) + tg(2700 +α) + ctg(3600 +α) б) sin( в) sin2(1800 - α) + sin2(2700 - α) г) sin(π - α) cos(α – д) е) ж) з)
Формулы сложения
1. С помощью формул сложения преобразуйте выражения а) cos( д) cos(600 + α) е) sin(600 + α) ж) cos((300 - α) з) sin(300 - α)
2. Представьте 1050 как сумму 600 + 450 и найдите сos 1050, sin1050 3.Представьте 750 как сумму 300 + 450 и найдите сos 750, sin750
4. Найдите значение выражения
5. Упростите выражение
6. Докажите, что а) sin(α + β) + sin(α – β) = 2 sin α cos β б) cos(α – β) + cos(α + β) = 2 sin α sin β в) sin(α + β) · sin(α – β) = sin2 α – sin2 β г) cos(α – β) · cos(α + β) = cos2 α – cos2 β
Формулы суммы и разности тригонометрических выражений 1. С помощью формул преобразования суммы тригонометрических функций в произведение разложите на множители:
2. Представьте в виде произведения: а) sin 120 + sin 200 б) cos 400 – cos 160 в) sin 520 – sin 320 г) cos150 + cos 650 д) sin 500 + sin 800 2. Упростите выражение:
Формулы двойного угла. Упростите выражение
2. Сократите дробь а) 3. Упростите а) 4. Упростите выражение
5. Вычислите
6. Пусть sinα =
7. Пусть sinα = -0,6 и α угол третей четверти. Найдите cos2α; sin2α; tg2α
8. Пусть cosα =-0,8 и α угол второй четверти. Найдите cos2α; sin2α; tg2α
9. Докажите тождество
2. 7. Преобразование тригонометрических выражений.
1. –tg2α – sin2α + 2. 3. –ctg2α – cos2α + 4. 5. tg2α + sin2α - 6. ctg2α + cos2α - 7. (sinα + cosα)2 - sin2α 8. 9. 10. sin4α – cos4α + cos2α 11. (3 + sinα)(3 - sinα) + (3 + cos α)(3 - cos α) 12. 4· 13. 14. (ctgα + tgα)(1 + cosα)(1 – cosα) 15. 16. 6· Форма отчетности. Письменная работа. Самостоятельная работа по каждому разделу. Контрольные вопросы. 1. Дайте определения основных тригонометрических функций 2. Запишите формулы, связывающие значения тригонометрических функций одного аргумента 3. Как зависят знаки тригонометрических функций в зависимости от координатной четверти. 4. Значения тригонометрических функций основных углов. 5. Основное тригонометрическое тождество, связь тангенса и косинуса, связь котангенса и синуса, произведение тангенса и котангенса. 6. Формулы приведения 7. Формулы двойного угла. 8. Формулы суммы и разности тригонометрических выражений 9. Формулы сложения. Литература. лекции, информационно - поисковая система Интернет https://www.akademia-moskow.ru/ учебник М.И.Башмаков «Математика» учебник, задачник. Оценка результатов работы. Выборочная оценка. Контрольная работа по теме ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 3 Тема: Тригонометрические функции и уравнения Цель: рассмотрение всех всевозможных способов преобразования графиков функций, научиться решать тригонометрические уравнения, используя свойства обратных тригонометрических функций и формул решения тригонометрических уравнений.
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-08-19; просмотров: 477; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.70.64 (0.008 с.) |

 < α < π
< α < π ; в) cos α = -
; в) cos α = -  ; г) ctg α = -2;
; г) ctg α = -2;  ; в) tg α = 3;
; в) tg α = 3;  ; д) sinα =
; д) sinα =  ; е) cos α =
; е) cos α =  ;
; и
и 
 и
и  ;
л)
;
л)  ;
м)
;
м)  ;
н) sin2 α + cos2 α + tg2 α;
о) tg α• сtg α + сtg2 α;
;
н) sin2 α + cos2 α + tg2 α;
о) tg α• сtg α + сtg2 α;
 б)
б)  - 1;
в) 1 -
- 1;
в) 1 -  ;
г)
;
г)  ;
д) ctg β -
;
д) ctg β -  ;
;
 ;
ж)
;
ж)  ;
з)
;
з)  ;
и)
;
и)  ;
к) cos2 α – (ctg2 α +1)• sin2 α.
;
к) cos2 α – (ctg2 α +1)• sin2 α.
 ;
б)
;
б)  ;
;
 ;
г)
;
г) 
 ; в) cos2 α • tg2 α – 1
; в) cos2 α • tg2 α – 1 =
= 
 =
= 
 - α)
б) cos(
- α)
б) cos( + α)
в) tg(
+ α)
в) tg( )
б) cos(α – π)
)
б) cos(α – π)
 - α)
- α)



 - α)
б) cos(
- α)
б) cos( + α)
в) tg(
+ α)
в) tg( ; б) sin(
; б) sin( ; г) sin(
; г) sin( - α) –
- α) –  cos α
б)
cos α
б)  sinβ + cos(α -
sinβ + cos(α - 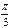 )
)
 cosα – 2cos(α -
cosα – 2cos(α -  )
г)
)
г)  sin(
sin( + α) – cos α
+ α) – cos α




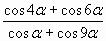

 б)
б) 
 г) cos2α + sin2 α
г) cos2α + sin2 α

 б)
б)  в)
в)  г)
г) 
 б)
б)  в)
в)  г) sin2 α + cos2α
г) sin2 α + cos2α б)
б) 

 cos
cos  – sin2
– sin2  ж) 2 sin1650 cos1650
з) cos2750 – sin2750
ж) 2 sin1650 cos1650
з) cos2750 – sin2750
 и α угол второй четверти. Найдите cos2α; sin2α; tg2α
и α угол второй четверти. Найдите cos2α; sin2α; tg2α












