
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятние экономического риска. Меры риска.Содержание книги
Поиск на нашем сайте
Любое коммерческое предприятие в своей деятельности постоянно сталкивается с рисками, т.е. угрозами финансовых потерь под воздействием внутренних и внешних факторов; именно поэтому залогом его успешного функционирования является способность управлять рисками в конкретных макроэкономических условиях. Но для того, чтобы управлять рисками, необходимо прежде всего определить само понятие риска и указать способы его измерения. Риск − одна из важнейших концепций экономической деятельности, однако по поводу риско существует немало заблуждений, связанных с непониманием их объективной природы. В наиболее общем понимании риск экономического субъекта (под экономическим субъектом подразумевается коммерческая организация либо индивидуальный предприниматель представляет собой неопределенность (неоднозначность) его экономических результатов в будущем, обусловленную неопределенностью (неоднозначностью) самого этого будущего. И поскольку риск − это неопределенность (случайность), то измерение риска − это измерение неопределенности, для чего наиболее естественно использовать вероятностную модель. В дальнейшем будем предполагать, что качество вырабатываемых управленческих решений оценивается с помощью одного финансового показателя Х − дохода, величины чистого приведенного потока прибыли или объема затрат, из которых первые два подлежат максимизации, а третий −минимизации. В условиях риска любой из этих показателей становится случайной величиной, которая может быть охарактеризована и оценена с помощью математического аппарата теории вероятностей. Несмотря на определенную популярность темы рисков в экономике, до настоящего времени не сформировался единый подход к методам измерения рисков; более того, нет и единой, устоявшейся терминологии. Так, в экономической теории и практике риском называют как вероятностные характеристики случайного события: вероятность получения определенной прибыли или вероятность определенного объема затрат (реже), так и масштабную величину результата этого события (чаще). Возможно, правильнее было бы называть риском именно вероятностные характеристики как меру неопределенности принимаемых решений, а масштабные показатели именовать иначе, например, позицией или ценой риска. В дальнейшем применяется общепринятая терминология, допускающая двоякое понимание меры риска, а там, где возможна неоднозначная трактовка, сделаны соответствующие оговорки. Мера риска − это абсолютная (относительная) величина или вероятностный показатель возможных результатов хозяйственной деятельности экономического субъекта в заданных условиях в течение определенного периода времени в будущем. Абсолютная величина результатов выражается в денежной форме и характеризует их среднее значение или разброс относительно среднего значения; относительная величина может быть выражена в процентном отношении к вложенным средствам. В качестве вероятностной характеристики меры риска традиционно используют закон распределения случайной величины, устанавливающий связь между возможными значениями случайной величины и вероятностями их реализации (и здесь нет единства подходов: под вероятностной мерой риска обычно понимают вероятность получения определенной прибыли, хотя здесь более уместным является термин «надежность», и вероятность того, что прибыль не будет получена). Закон распределения может быть представлен рядом распределения, кривой распределения и функцией распределения.
По известным значениям вероятностей можно рассчитать кумулятивную функцию распределения случайной величины Х, численно равную вероятности того, что значение Х меньше х (последняя строка табл.): F x (x)=P(X<X)=
При любом подходе, вероятностном или масштабном, риск имеет математически выраженную вероятность наступления определенного события, которая опирается на статистические данные или экспертные оценки и может быть рассчитана с достаточно высокой степенью точности. Среднее ожидаемое значение (математическое ожидание) случайной величины Х выражается в денежных единицах, обозначается МХ и вычисляется как взвешенно среднее для всех различных ее значений, где вероятность каждого значения используется в качестве весового коэффициента. В терминах введенных выше обозначений: MX= Математическое ожидание − это еще не оценка риска как такового, это значение показателя Х, по которому оценивается качество принимаемых управленческих решений, вычисленное с учетом риска. Однако, зная среднюю ожидаемую прибыльность проекта и имея закон распределения прибыли FA (x), можно построить и обобщенную вероятностную характеристику риска. Под риском проекта А естественно понимать вероятность того, что полученная прибыль будет меньше средней: rA = P { X < x } = FA (x). Среднее значение представляет собой одну из обобщенных масштабных характеристик случайной величины и зачастую не дает возможности принять решение в пользу какого-то способа действия. Для более обоснованного выбора необходимо измерить колеблемость показателей, т.е. определить меру изменчивости возможного результата. Так, при вложении средств в некоторый проект важно знать не только среднюю величину прибыли, но и пределы, в которых она может меняться. Колеблемость возможных результатов представляет собой степень отклонения случайной величины от среднего значения. Для ее оценки на практике применяют три тесно связанных между собой показателя: дисперсию, стандартное отклонение и коэффициент вариации, каждый из которых может быть использован как оценка непосредственно риска принимаемого решения (отклонение от ожидаемого значения в абсолютном или относительном измерении). Дисперсия − это взвешенно среднее квадратов отклонений возможных значений случайной величины от ее ожидаемого значения: DX= M(X- MX)2≥0 DX= M(X2)-(MX)2 M(X2)= Так же, как и среднее значение, дисперсия является именованной величиной; ее размерность равна квадрату размерности самой случайной величины и потому использовать дисперсию для оценки разброса случайной величины не вполне удобно. В связи с этим, наряду с дисперсией, вводится стандартное отклонение σ X = Стандартное отклонение служит мерой абсолютной колеблемости. Наряду с дисперсией и среднеквадратическим отклонением в качестве меры риска используют также полудисперсию, при вычислении которой учитываются только те состояния, в которых доходность ниже ожидаемой: SDX= Удобной безразмерной характеристикой случайной величины, котораяпоказывает относительное значение ее разброса, является коэффициент вариации: VX= до 0.1 − слабая вариабельность; 0.1−0.25 − умеренная вариабельность; свыше 0.25 − высокая вариабельность. 17 Критерий Байеса
Критерий Байеса (принцип математического ожидания) предполагает полное доверие ЛПР известным вероятностям состояний окружающей среды. Следовательно, данная задача – это задача принятия решения в условиях риска.
Показатель эффективности стратегии Аi по критерию Байеса находится по формуле:
Z =,
гдеm – количество строк матрицы, заданной в условии;
n – количество столбцов матрицы, заданной в условии;
qj – заданные вероятности;
аij – элементы матрицы, заданной в условии.
Для случая оптимизации потерь критерий будет таким:
Z = #
Заметим, что – это математическое ожидание стратегии Аi. Таким образом, исходную матрицу необходимо дополнить справа еще одним столбцом, в который нужно внести значения математических ожиданий всех стратегий:
Пример вычислений для первой строки:
= 0,33 + 0,27 + 0,153 + 0,115 + 0,256 = 0,6 + 1,4 + 0,45 + 1,5 + 1,5 = 5,75
Далее в добавленном столбце нужно найти наибольший элемент (наибольшее математическое ожидание). Строка, в которой он стоит и будет оптимальной стратегией. Необходимо заметить, что наибольших элементов может быть несколько, тогда и оптимальных стратегий соответственно будет несколько.
В нашем случае наибольший элемент 5,95 (в матрице он выделен). Таким образом, в нашем примере оптимальной стратегией будет А3, т.е. средства фонда вам нужно вложить в третий проект.
Ответ А3. 18
МЕТОД «ДЕРЕВА РЕШЕНИЙ» Оценка альтернатив в случае, когда действие, предпринимаемое на одной стадии, зависит от действия, предпринятого на предыдущей, является достаточно сложной. Построение «дерева решений» чаще всего используется для анализа проектных рисков. Метод применяется для тех проектов, которые имеют обозримое количество вариантов развития. При этом аналитик, осуществляющий построение «дерева решений», для формулирования различных сценариев развития проекта должен обладать необходимой и достоверной информацией с учетом вероятности и времени их наступления. Можно предложить следующую схему управления проектом, последовательности сбора данных для построения «дерева решений»:
определение состава и продолжительности фаз жизненного цикла проекта; определение ключевых событий, которые могут повлиять на дальнейшее развитие проекта; определение времени наступления ключевых событий; формулировка всех возможных решений, которые могут быть приняты в результате наступления каждого ключевого события; определение вероятности принятия каждого решения; определение стоимости каждого этапа осуществления проекта (стоимости работ между ключевыми событиями) в текущих ценах. На основании полученных данных строится «дерево решений», структура которого содержит узлы, представляющие собой ключевые события (точки принятия решений), и ветви, соединяющие узлы, - работы по реализации проекта. В результате построения «дерева решений» рассчитываются вероятность каждого сценария развития проекта, NPV по каждому сценарию, а также ряд других принципиально важных показателей.
Следует отметить, что очень часто по различным причинам, в значительной мере в связи с отсутствием достоверной информации, использование статистического метода или метода «дерева решений» не представляется возможным. В таких случаях применяются методы, использующие результаты опыта и интуицию, то есть эвристические методы или методы экспертных оценок.
Пример, основанный на методе построения дерева решений В более сложных ситуациях в анализе используют так называемый метод построения дерева решений. Логику этого метода рассмотрим на примере. Пример: управляющему автосервису «Арьат-Авто» нужно принять решение о целесообразности приобретения станка М1 для проведения работ «сход-развал» либо станка М2. Станок М2 более экономичен, что обеспечивает больший доход на единицу обслуживаемой техники, вместе с тем он более дорогой и требует относительно больших накладных расходов:
Постоянные расходы (в у.е.) Операционный расход на единицу обслуживаемой техники (в у.е.) Станок М1 15000 20 Станок М2 21000 24
Процесс принятия решения может был выполнен в несколько этапов: Этап 1. Определение цели.
В качестве критерия выбиралась максимизация математического ожидания прибыли. Этап 2. Определение набора возможных действий для рассмотрения и анализа (контролируются лицом, принимающим решение) Управляющий может выбрать один из двух вариантов: а1 = {покупка станка М1} а2 = {покупка станка М2} Этап 3. Оценка возможных исходов и их вероятностей (носят случайный характер). Управляющий оценивает возможные варианты годового спроса (кол-во обслуживаемых автомобилей) на продукцию и соответствующие им вероятности следующим образом: х1 = 1200 единиц с вероятностью 0.4 х2 = 2000 единиц с вероятностью 0.6 Этап 4. Оценка математического ожидания возможного дохода:
Е (Да) = 9000 * 0. 4 + 25000 * 0. 6 =8600 Е (Дб) = 7800 * 0. 4 + 27000 * 0. 6 = 19320 Таким образом, вариант с приобретением станка М2 экономически более целесообразен. Решение принимается в условиях неопределённости, когда из-за недостатка информации невозможно количественно оценить вероятность его возможных результатов. Это довольно часто встречается при решении новых, нетипичных проблем, когда требующие учёта факторы настолько новы и/или сложны, что о них невозможно получить достаточно информации. Неопределённость характерна и для некоторых решений, которые приходится принимать в быстро меняющихся ситуациях. В итоге вероятность определённой альтернативы невозможно оценить с достаточной степенью достоверности. Сталкиваясь с неопределённостью, управляющий может использовать две основные возможности: 1) попытаться получить дополнительную информацию и ещё раз проанализировать проблему с целью уменьшить её новизну и сложность. В сочетании с опытом и интуицией это даст ему возможность оценить субъективную, предполагаемую вероятность возможных результатов; 2) когда не хватает времени и / или средств на сбор дополнительной информации, при принятии решений приходится полагаться на прошлый опыт и интуицию.
?.Критерии принятия рискованных решений Рассматриваемая в настоящем разделе проблема в общем виде формулируется следующим образом. Принимающий решение должен выбрать одну из имеющихся альтернатив Ai i = 1,2,K, m, каждая из которых в конечном счете будет иметь своим результатом некоторый исход, набор которых считается известным и зависящим от состояний природы Qj, j = 1,2,K, n. Оценка предпочтительности возможных исходов осуществляется с помощью одного критерия Х (доход или затраты). Принимающий решение не знает точно, к какому именно исходу приведет любая из выбранных им альтернатив, но для каждого способа действия он в состоянии установить вероятности реализации различных исходов. Информация для принятия решения представляется таблицей
F(Ai Qj) aij
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-05-20; просмотров: 688; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.138.214 (0.008 с.) |

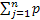 j=1
j=1
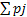 , j:xj<x
, j:xj<x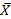 =
= 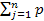 jxj
jxj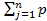 jxj2
jxj2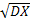 , которое измеряется в тех же единицах, что и сама случайная величина.
, которое измеряется в тех же единицах, что и сама случайная величина.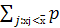 j( xj-
j( xj- 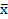 )2
)2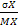 , который показывает, какую долю среднего значения случайной величины составляет ее средний разброс. Коэффициент вариации – относительная величина, на его размер не оказывают влияния абсолютные значении изучаемого показателя. С помощью коэффициента вариации можно сравнивать даже показатели, измеренные в различных денежных единицах. Коэффициент вариации меняется в пределах от 0 до 1 и чем больше его значение, тем больше вариабельность случайной величины. В экономической статистике принята:
, который показывает, какую долю среднего значения случайной величины составляет ее средний разброс. Коэффициент вариации – относительная величина, на его размер не оказывают влияния абсолютные значении изучаемого показателя. С помощью коэффициента вариации можно сравнивать даже показатели, измеренные в различных денежных единицах. Коэффициент вариации меняется в пределах от 0 до 1 и чем больше его значение, тем больше вариабельность случайной величины. В экономической статистике принята:


