
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постановка задачи управления рисками.Основные приемы снижения экономического риска. ⇐ ПредыдущаяСтр 8 из 8
Можно охарактеризовать как совокупность методов, приемов и мероприятий, позволяющих анализировать наступление рискованный событий и принимать меры, и адекватному реагированию на эти события. Управление рисками в широком смысле и представляет собой особый вид деятельности направленных с одной стороны на смягчение воздейств на влияние налогооблагаемых факторов, результаты бизнеса, а с другой стороны- на использование благоприятного влияния этих факторов обеспечив дополнительные полезные результаты. В более узком смысле управление рисками сводится к обеспечению безопасности ЛПР наоснове учета неблагоприятных факторов, снижении или ликвидации самих этих факторов или последствия их влияния. Методы снижения риска: - методы уклонения - методы локализации - методы дискриминации - методы компенсации.
?. Планирование эксперимента или принятия рисковых решений. Пусть информация необходимая для принятия решений с условиях риска задается статистической …… с платежной матрицей А, без получения дополнительной информации ЛПР выбирает решение руководствуясь критерием Байеса. Каждая стратегия Аi оценивается срдним ожиданием результатом в качастве оптимальной выбирается стратегия доставления максимальной цели Max ai (A- выигрыш), min ai (A - проигрыш) Предположим,что ЛПР планирует провести эксперимент для умножения иск. Инф. О ситуации принятия решения.эксперимент считается идеальным если после его проведения ЛПР точно знает??? состояния природы необходимо оценивать целесообразность проведения планового эксперимента. А- выигрыш, Bj - -max (i=1,m) Максимальный элемент j –столбца матрицы А или максимальный проигрыш в j состоянии природы.
Взвешенно средняя маскимальный выигрыш где в качестве весовых коэффициентов использованы вед-ти состояния природы. Увт. 1 Идеальный эксперимент стоимостью с денеж ед. целесообразно проводить в случае когда
Утв. 2 Идеальный эксперимент стоимостью с денеж ед. целесообразно проводить:
?. Функции полезности До сих пор обоснование выбора решений осуществлялось с позиций объективиста, платежи выражались в форме реальных денег. Имеются многочисленные случаи, когда при анализе следует использовать скорее полезность, чем реальную величину платежей. Определение полезности является субъективным, оно зависит от отношения ЛПР к риску.
Для составления представления о склонности или несклонности к риску наиболее пригодно понятие простого шанса или простой лотереи, под которой понимается лотерея с двумя исходами, вероятности которых известны и в сумме равны 1, а также понятие гарантированного эквивалента, под которым понимается такой гарантированный доход, который для данного ЛПР эквивалентен простому шансу. Простой шанс представляется набором L = { x 1, x 2, p }, где х 1 − выигрыш с вероятностью р, х 2 − выигрыш с вероятностью (1 − р), x 1 > x 2. Например, если из 1000 лотерейных билетов 1 приносит выигрыш 1 млн. руб, а остальные – ничего, то такая лотерея представляет собой простой шанс вида L = {1, 0, 0.001} Под гарантированным эквивалентом понимают сумму, которую ЛПР согласно заплатить за право участия в простой лотерее. Склонность или несклонность ЛПР к риску определяется в зависимости соотношения ожидаемого выигрыша в простую лотерею и гарантированного эквивалента В. Если гарантированный эквивалент В больше ожидаемого выигрыша в простую лотерею: px 1 + (1− p) x 2 < B и ЛПР согласен заплатить сумму, равную В, за право участия в данной лотерее, т.е. за (100 р)% -й шанс выиграть х 1 д.е., то он считается склонным к риску. Если гарантированный эквивалент меньше ожидаемого выигрыша в простую лотерею, т.е. px 1 + (1− p) x 2 > B и ЛПР согласится заплатить за право участия в лотерее только В, то он не склонен к риску. Если гарантированный эквивалент для ЛПР совпадает с математическим ожиданием выигрыша в простую лотерею: px 1 + (1− p) x 2 = B, то ЛПР безразличен (нейтрален) к риску. Определим функцию полезности на лотерее L = { x 1, x 2, p }: u (x 1, x 2, p) = pu (x 1) + (1− p) u (x 2). Соответствие лотереи гарантированному эквиваленту означает, что их полезность для ЛПР одинакова: u (B) = u (x 1, x 2, p) = pu (x 1) + (1− p) u (x 2). Учитывая, что функция полезности является возрастающей, получаем: если ЛПР склонен к риску, то u (B) = pu (x 1) + (1− p) u (x 2) > u (px 1 + (1− p) x 2), и график функции полезности u (x) является выпуклым вниз;
если ЛПР не склонен к риску, то u (B) = pu (x 1) + (1− p) u (x 2) < u (px 1 + (1− p) x 2), и график функции полезности u (x) является выпуклым ввер если ЛПР безразличен к риску, то u (B) = pu (x 1) + (1− p) u (x 2) = u (px 1 + (1− p) x 2) (37) и функция полезности u (x) линейна. Рассмотрим влияние свойств функций полезности на однозначность выбора оптимального решения на примере задачи о страховании. Почему одни люди страхуются, а другие нет? Кто принимает оптимальное решение, а кто ошибается? Оказывается, никто не ошибается, а все принимают оптимальные решения. Только это оптимальное решение является разным для различных типов функций полезности, т.е. не существует единственного оптимального решения. Пусть финансовое состояние индивидуума оценивается заданным значением W. Предполагается, что можно вычислить вероятность р потери некоторой части этого богатства, измеряемой величиной L ≤ W (например, в результате несчастного случая). Индивид может купить страховой полис, в соответствии с которым ему возместят нанесенный ущерб в размере q. Плата за страхование составляет π q, где π − доля страхования в объеме нанесенного ущерба. Проблема состоит в определении значения q. Исследуем задачу максимизации ожидаемой полезности финансового состояния индивидуума в ситуации, когда с вероятностью р страховой случай происходит и с вероятностью (1 − р) − не происходит. Тогда задача сводится к поиску максимума по q ожидаемой полезности капитала индивида: [ pu (W − L − π q + q) + (1− p) u (W – π) Применим необходимое условие оптимальности − продифференцируем выражение в квадратных скобках и приравняем производную к нулю предполагается, что функция полезности вогнута − ЛПР не склонен к риску): [ pu ′(W − L − π q + q)(1− π) + (1− p) u ′(W − π q)(− π)] = 0. Оптимальное значение q находится как решение получившегося уравнения в предположении, что вид функции полезности известен. Рассчитаем ожидаемую прибыль страховой компании, учитывая, что страховой случай имеет вероятностный характер. Если страховой случай произошел, компания получает доход (π q − q), иначе ее доход равен π q, ожидаемая прибыль страховой компании равна q (π − p). Конкуренция между страховыми компаниями уменьшает прибыль, которая в условиях совершенной конкуренции стремится к нулю, т.е. π ≈ p. Если это соотношение ввести в условие ожидаемой полезности, получим u ′(W − L + (1− π) q *) = u ′(W − π q *). Если ЛПР не склонен к риску (вторая производная функции полезности отрицательна), то из равенства первых производных следует равенство аргументов: q * = L, т.е. страховаться целесообразно на сумму возможного ущерба. ?. Постановка задачи коллективного выбора. Под групповым выбором понимают процедуру принятия коллективных решений, на основе принятия предпочтений членов группы Полное рассмотрение группового выбора предполагает решение проблем организации процедур коллективного мнения и … того как из индивидуальных мнений формируется коллективное предпочтение. Постановка задачи группового выбора: Пусть имеется коллектив состоящий из N человек и называется экспертами. N=(а1,а2,…n) Имеется так же множество альтернативных вариантов решений.
Предполагается, что каждый из экспертов линейно упорядочить альтернативы в соответствии с собственными предпочтениями А= (а1,а2,…m) При этом коллективные оценки альтернатив не предполагаются и в случае безразличия не исключаются. В простейших случаях считают, что мнение экспертов выражено колличествено, например в баллах. Uj (аj) оценка выставленная j экспертом альтернативе aj, тогда коллективная оценка представлена вектором. U1(aj),U2(aj)…Un(aj) Задача группового выбора состоит в построении обобщенной оценки U по известным предпочтениям членов группы.
?. Схемы голосования. Наиболее распространенным принципом группового выбора является принцип большинства реализованный в процедурах голосования. Под голосованием понимают процедуру, содержащую следующее: элементы, каким-то образом сформулированы набором вариантов, заданному в бюллетени. Отражение каждым участником его мнения происходит в соответствии с инструкцией, а коллективное мнение формируется на основе информации, содержащейся в бюллетенях. В коллективном ЛПР могут образовываться коалиции, т.е. участники с совпадающими интересами. Наиболее распространенными принципами формирования коллективного мнения явл. принцип большинства. 1. Правило относительного большинства – побеждает альтернатива, получившая наибольшее количество голосов. 2. Правило простого большинства – каждый эксперт имеет 1 голос, лучшей является альтернатива, набравшая большее количество голосов. Если таковая отсутствует проводится 2-ой тур, в который входит 2 лучшие альтернативы из 1-го тура и среди них выбирается лучший вариант. Эти правила не всегда выявляют победителя. Основная проблема состоит в том, что в этих процедурах может возникнуть эффект зацикливания, который называется парадоксом Кандрасе.. Правило суммы мест – альтернатива, поставленная экспертом на 1-е место, получает 1 балл, на второе – 2 балла и т.д., победителем является та альтернатива, которая в сумме набрала меньше баллов. Правило Кандрасе – наилучшей считается альтернатива победившая в наибольшем числе сравнений с другими альтернативами
Результаты коллективного выбора зависят не только от индивидуальных предпочтений, но и от процедура обработки результатов, которую необходимо подбирать для каждой конкретной ситуации Необходимо указать правил, по которым это коллективное мнение, соответствующие требования формируются в виде аксиомы:
1 Аксиома полноты - любые 2 альтернативы сравнимы между собой, т.е для любой из альтернатив выполняется одно из 3-х условий: а лучше б, б лучше а или равнозначны. 2. Аксиома транзитивности – если а лучше б и лучше с, то а лучше с. 3. Аксиома единогласия - если все эксперты считают, что а лучше б, то с точки зрения коллектива а лучше б. 4. Аксиома независимости – положение 2-х альтернатив зависти только от их оценки отдельными индивидами и не зависит от других альтернатив. Обосновано, что существует правило, которое удовлетворяет все эти 4 аксиомы
[1] Предисловие к книге Саати Т. Принятие решений. Метод анализа иерархий. М.: Радио и связь, 1993. [2] Фоменко Н.А. Вариант практического применения метода анализа иерархий при согласовании результатов расчета в процессе оценки // http://anf-ocenka.narod.ru/35.pdf
|
||||||||
|
Последнее изменение этой страницы: 2019-05-20; просмотров: 243; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.201.71 (0.019 с.) |
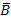 =
= 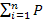 jBj
jBj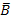 -
- 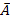 > C нецелесооб-но:
> C нецелесооб-но: 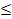 C
C 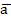
 > c –нецелесооб.
> c –нецелесооб.



