
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Составитель: пазынич Г. И канд. Техн. Наук, доцент, кафедры “судовождение и промышленное рыболовство” фгбоу во «кгмту»Содержание книги
Поиск на нашем сайте
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «КЕРЧЕНСКИЙ ГОСУДАРСТВЕННЫЙ МОРСКОЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра «Судовождение и промышленное рыболовство»
Пазынич Г.И. ПРОМЫСЛОВАЯ НАВИГАЦИЯ МЕТОДИЧЕСКИЕ УКАЗАНИЯ по самостоятельной работе и по выполнению расчетно-графической работы для курсантов специальности 26.05.05 «Судовождение» Очной формы обучения
Керчь, 2017 г. УДК 639.2.052.1 Составитель: Пазынич Г.И канд. техн. наук, доцент, кафедры “Судовождение и промышленное рыболовство” ФГБОУ ВО «КГМТУ» _______________________
Рецензент: Новоселов Д.А. ст. преподаватель кафедры “Судовождение и промышленное рыболовство” ФГБОУ ВО «КГМТУ» ________________
Методические указания рассмотрены и одобрены на заседании кафедры “Судовождение и промышленное рыболовство ФГБОУ ВО ” КГМТУ». протокол № 5 от «14» 12. 2017 г. Зав. кафедрой ______________ Н.В. Ивановский
Методические указания рассмотрены и рекомендованы к публикации на заседании учебно-методической комиссии МФ ФГБОУ ВО ” КГМТУ». протокол № 3 от «14» 12. 2017 г.
ФГБОУ ВО «КГМТУ», 2017 г.
СОДЕРЖАНИЕ Стр. 1. ВВЕДЕНИЕ. 4 1.1 Указания по оформлению работ. 4 1.2 Индивидуальные задания на выполнение расчетно-графической работы. 5 1.3 Содержание и объем самостоятельной работы студента 6
2. Задания на решение задач промысловой навигации по первому разделу курса 8 2.1 Тема: «Построения траектории движения судна и трала» 8 2.2 Индивидуальные задания 8 2.3 Методические указания 10
3. Задания на решение задач промысловой навигации по второму разделу курса 12 3.1 Задание № 1. Оптимальная загрузка судна 12 3.2 Задание № 2. Выбор оптимального промыслово-технологического режима работы судна 13 3.3 Задание № 3 Решение задач методами теории игр 14 3.4 Задание № 4 Задачи по теории статистических решений 15 3.5 Задание № 5 Задачи по теории массового обслуживания 17 3.6 Задание № 6 Задачи на практическое занятие по теме «Управление запасами» 18 3.7 Вопросы подготовки к защите контрольной работы 19 3.8 Список рекомендуемой литературы 19
4. Примеры решения задач 21 4.1 Задача № 1 21 4.2 Задача № 2 24 4.3 Задача № 3 26
4.4 Задача № 4 28 4.5 Задача № 5 31 4.6 Задача № 6 33 5. Список вопросов для сдачи зачета по дисциплине "Промысловая навигация" 35 6. Учебно-методическое обеспечение 36
ВВЕДЕНИЕ Основной задачей расчетно-графической работы является закрепление практических навыков решения задач промысловой навигации. При этом достаточное внимание должно быть уделено также теоретическому обоснованию применения того или иного практического метода. Таким образом, контрольная работа позволяет подготовиться к применению различных методов решения различных задач управления промысловой работой судов в море. Отсутствие литературы по конкретному применению математических методов в задачах управления промыслом требуют от исполнителя расчетно-графической работы тщательного и целеустремленного изучения такого материала во время занятий в институте. Наибольшую трудность при выполнении контрольной работы представляет творческое применение общеизвестных и специальных математических методов к решению конкретных промысловых задач. При этом наиболее эффективным является путь, когда на основе практического опыта решения той или иной промысловой задачи в аудитории разрабатывается математическая модель и способ решения однотипной, но «своей» промысловой задачи. В наихудшем случае при отсутствии «своей» промысловой задачи можно применить решение уже известной промысловой задачи, но по своим твердо обоснованы исходным данным. Решение каждой задачи обязательно заканчивается анализом полученного результата с позиции его реализации на практике, с подробным указанием соответствующих организационных мероприятий или промысловых действий. Глубина анализа полученного результата показывает инженерную зрелость разработчика, всестороннее понимание рассматриваемой производственной ситуации. Индивидуализация заданий обеспечивается за счет решения промысловых задач на судах определенного типа, в различных районах промысла при лове различных видов гидробионтов. При отсутствии в задании конкретных числовых показателей работы судна для расчетов применяются среднестатистические величины. Задания на расчетно-графическую работу приводится в таблице 1 по двум последним цифрам номера зачетной книжки.
Задания для курсантов очной формы обучения выбираются по цифрам индивидуального задания в соответствии с порядковым номером шифра. Из раздела 1 выбирают условия для решения задач №1, №4, №5. Из раздела 2 выбирают условия для решения задач по индивидуальным задачам №1, №4, №5.
УКАЗАНИЯ ПО ОФОРМЛЕНИЮ РАБОТ Все записи выполнять в соответствии с требованиями оформления технической документации, по возможности с печатаньем текстовой части. Каждый раздел расчетно-графической работы следует оформлять как самостоятельную часть, включающую соответствующее число параграфов. Раздел 2 может содержать только три из всех перечисленных задач. Решение отдельных задач или примеры применения различных математических методов должны содержать математическую модель задачи или ситуации в общем виде, краткое обоснование выбранных числовых параметров задачи. Условия в стандартных обозначениях записываются колонкой в левой части листа. Справа записываются расчетные формулы и цифровые данные расчетов. В тех случаях, когда для решения использовались вспомогательные графические материалы (диаграммы, планшеты, расчетные бланки и т.д.) результаты графических построений показывают схемой этих построений или прилагаются в полном объеме на кальке или на диаграмме, планшете и т.д. При решении одной задачи несколькими способами результаты существенных расхождений в ответах должны иметь письменное объяснение. Каждый раздел расчетно-графической работы выполняется на отдельных листах с обязательным анализом полученных результатов и практическими рекомендациями по их использованию. Порядок расчетов и графических построений при решении задач каждого типа рассмотрен на лекциях и приведен в методических указаниях по выполнению соответствующих практических занятий. Обоснование принятого способа решения задачи должно содержать указания о характере взаимосвязей между параметрами задачи или промысловой ситуации. Принятые к расчету цифровые величины должны соответствовать определенным типам судов и районам промысла, породному составу уловов. При отсутствии таких данных используют условные величины, учитывая тесноту их взаимосвязей и влияние на каждый результат. После выполнения всех расчетов полученный результат проверяется на оптимальность. Анализ результата также проводится для определения тех ограничений в начальных условиях задач, которые определили результат. Заканчивается анализ проверкой зависимости результата от исходных данных, определением тех возможных изменений данных, которые допустимы в данных условиях, т.е. не приведут к изменению результата. Одновременно при этом определяются все особенности решения задачи: возможность усовершенствования расчетного алгоритма, адекватность математической модели реальным условиям промысла. 1.2 Индивидуальные задания на выполнение Продолжительность 6 ч. Пособия и инструменты:
1. Навигационные планшеты 2. Прокладочный инструмент 3. Журнал практических работ 4. МК 5. Конспект лекций
2.2 Индивидуальные задания Задание № 1. Определить траекторию движения судна и трала после изменения курса на 600 вправо при расчетах учесть следующие условия плавания:
По результатам решения определить боковое смещение трала через 12 и 24 минуты после маневра, время выхода трала на новый курс движения судна, необходимое время движения с изменением курса для обхода препятствия прямо под килем судна, маневр для выхода трала на косяк, который находится на КУ 300 левого борта и дистанции 6 кбт.
Задание № 2. Рассчитать маневр безопасного движения судна и трала при расхождении со встречным однотипным судном при следующих условиях плавания:
По результатам расчетов и построений составить схему маневрирования и таблицы МБР вашего судна при изменении курсов на 150, 300 и 450.
В таблицы включить:
Mtn Д для начала маневра Перетравливание ваеров Время нужное для расхождения судов Время нахождения трала вне курса судна Смещение судна с линии пути Смещение трала с линии пути Величину вектора смещения
Задание № 3. В момент Т=00.00, когда по результатам решения предыдущей задачи трал вышел на продолжение ДП судна, прямо по носу (на КУ) обнаружили новый косяк на Д0= 1600 м. начато с ним сближение кривой погони. В момент Т=00,06, когда курс судна изменился на 200, 300 и 400, измерено расстояние до ядра косяка 800м. Определить с помощью таблиц курс и скорость косяка.
Vk=K*V; Kk=Kc+gK
Рассчитайте длину забега судна при условии, что постановка трала должна начинаться с расчетом перемещения косяка на курсе траления противоположном направлении движения судна. qk=Пк-Кк; sinY=(Vk/V)sin(gk)
Таблица значений К и gk для входного аргумента Д: До= 0,5
Задание № 4. Следуя курсом Кс=82 на Кус= 28 правого борта и Д1 обнаружен косяк рыбы.
Продолжая следовать прежним курсом со скоростью 9 узл. Через 6 минут измерили КУ=42 и Д2. Определить элементы движения косяка, угол упруждения и курс судна для выхода на косяк.
Задание № 5. Траектория движения судна и трала на циркуляции Прямая задача: Следуя курсом и скоростью (задание № 1) с тралом в ДП начали плавный поворот вправо (влево) с изменением начального курса на 1520 при Rc=3, кбт. Построить траекторию трала судна. Обратная задача: Рассчитали точку начала поворота для выхода судна строго на заданную линию движения и начали циркуляцию для выхода судна на нее. Построили траекторию движения судна и трала. Заданную линию движения проводит преподаватель после решения прямой задачи.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ Траектория трала, апроксимируемая трактрисой прямой линии, может быть построена для конкретного случая приближенным графическим способом. На линии нового курса судна выбирают ряд точек а, Ь, с, d и т. д., расположенных на одинаковом и достаточно малом расстоянии одна от другой (рис. 177). Соединяют точку а прямой линией с точкой Т (середина устья трала) и откладывают на этой линии отрезок аа', равный L. Затем соединяют точку Т прямой линией с точкой а' и откладывают на этой линии отрезок bb'=L. Аналогичным образом находят точки с', d' и т. д. Соединив точки Т, а', Ь', с', d' и т. д. согласной кривой, получают трактрису прямой линии.
Рисунок 2.1 Построение трактрисы
При прицельном облове локальных и в особенности быстроподвижных косяков рыбы курс траления должен определяться с учетом бокового уклонения трала после поворота судна. Так как трал выйдет на линию курса после того, как судно пройдет новым курсом некоторое расстояние 5, возникает вопрос: при каком расстоянии от точки встречи трала и ядра (центра плотности) облавливаемого косяка при расчете курса прицельного траления необходимо учитывать траекторию трала? Из приведенных данных натурных наблюдений видно, что при изменении курса судна на углы до 60° учитывать траекторию трала необходимо, если расстояние от точки поворота судна, буксирующего трал, до точки встречи трала и ядра косяка не превышает удвоенного горизонтального отстояния трала от судна, т. е. если При обнаружении локального косяка, имеющего промысловое значение, впереди траверза на достаточно большом расстоянии Выше предполагалось, что учет траектории трала при прицельном тралении осуществляется путем использования различных математических моделей этой траектории. Следует, однако, иметь в виду, что положение трала относительно судна может быть определено и с помощью специальных приборов с гидроакустическим или кабельным каналами связи. Такие приборы в настоящее время разрабатываются. Кроме того, положение трала относительно судна может быть определено и с помощью некоторых современных рыбопоисковых гидроакустических станций. Как будет показано в следующей главе, наведение в горизонтальной плоскости трала на локальный косяк требует определения упрежденного положения трала относительно судна— положения на момент встречи с косяком. Поэтому упомянутые выше приборы не исключают необходимости использования при расчете курсов прицельного траления математических моделей траектории трала. Но они будут способствовать повышению точности прицельного траления.
При условии автоматизации процесса разноглубинного тралового лова наличие на судне специального прибора для определения положения трала относительно судна обеспечивает возможность точного наведения в плоскости горизонта трала на ядро локального косяка при условии апроксимации действительной траектории трала близкой к ней математической кривой. Это достигается периодической коррекцией курса траления.
3 ЗАДАНИЯ НА РЕШЕНИЕ ЗАДАЧ ПРОМЫСЛОВОЙ НАВИГАЦИИ ПО ВТОРОМУУ РАЗДЕЛУ КУРСА
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ ПО РЕШЕНИЮ ЗАДАЧ МЕТОДОМ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
ЗАДАНИЕ №1
Режима работы судна (Аналитическое решение)
А - суточная добыча, т K2 - коэффициент расхода сырья на 1 т. второго вида продукции. С1,С2,С3 - оптовая цена за 1 т. различного вида продукции. 1. Составить математическую модель задачи выбора оптимального технологического режима траулера по своим данным с учетом возможностей выпуска различных видов продукции в объеме 40, 20 и 2 т. и коэффициентов расхода сырья на выпуск 1 т. Готовой продукции соответственно 1,0 К2, 2,0. 2. Заполнить исходную симплекс-матрицу и выполнить необходимое число итераций для получения оптимального решения. 3. Проанализировать полученное решение с учетом заданных условий и возможных изменений условий (изменение цен, увеличения или уменьшения вылова и т.д.). 4.Составить и решить задачу выбора оптимального режима работы промыслового судна по опыту своей работы, если исполнитель работает судоводителем промыслового судна. Методика решения задач рассмотрена в конспекте лекций, в [1] стр. 109-131, [2], стр. 16-35, [3], стр 44-54, [4], стр. 132-136. ЗАДАНИЕ N 3 Индивидуальные задания на решение задач методами теории игр
1. Составить матрицу игры между «рыбаком» и «природой» по данным своих условий 2. Определить частоты применения стратегии «рыбака» и «природы» и цену игры между ними 3. Сделать анализ полученного решения и описать возможные способы реализации решения 4. Расширить матрицу до размеров 3х3 за счет доминирующих стратегий 4. Составить и решить пример расчетов лучшего вылова из опыта своей работы и проанализировать его результаты. Методика решения задач наиболее просто и сжато, рассмотрена в соответствующем разделе конспекта лекций, а также в [1] стр. 132-162, [2] стр. 87-97, [3] стр.110-114, [4] стр.130-158.
ЗАДАНИЕ N 4 ИНДИВИДУАЛЬНЫЕ ЗАДАЧИ ЗАДАНИЕ N5
ИНДИВИДУАЛЬНЫЕ ЗАДАЧИ Задание N 6 ИНДИВИДУАЛЬНЫЕ ЗАДАЧИ НА ПРАКТИЧЕСКОЕ ЗАНЯТИЕ ПО ТЕМЕ «УПРАВЛЕНИЕ ЗАПАСАМИ».
Определить значения go, to, lmin, Lmin и построить график l (g) для заданных условий промысла. Рассчитать увеличение общих потерь при g1=1,5*go, а также при возможном вылове за сутки B2=0,75*В. В таблице обозначено: Co - промысловые затраты на вылов 1 т. сырья в грн/тонну. В -производительность рыбцеха в т/сутки. m -коэффициент потери качества сырья за час хранения 1т. рыбы. Qp -оптовая цена 1т. мороженной рыбы в грн. /тонну. Qm -оптовая цена 1т. рыбной муки в грн. на 1 тонну. Nср -среднее число тралений за сутки. Т -предположенное время стабильности промысловой обстановки в часах. Методические указания по применению методов управления запасами при решении задач тактики промысла приведены в конспекте лекций и в [3] стр. 68-86. ВОПРОСЫ ПОДГОТОВКИ К ЗАЩИТЕ КОНТРОЛЬНОЙ РАБОТЫ 1. Два пути повышения эффективности промысла, их использование на современном этапе. 2. Специфика управления промыслом, два типа задач управления промыслом отдельного судна и уровень их решения сейчас. 3. Существующие возможности научного решения задач управления промыслом. 4. Понятие о математическом программировании. Линейное и динамическое программирование. 5. Линейное программирование, общий порядок решения задач. 6. Выбор промыслово-технического режима работы. Формализация задачи. 7. Графическое решение задачи выбора режима работы. 8. Возможности использования линейного программирования при управлении промыслом. 9. Конфликтная ситуация, ее применение для задач управления промыслом. 10. Платежная матрица, пример ее составления. 11. Решение платежных матриц имеющих седловую точку. Цена игры. 12. Решение платежных матриц 2*2 не имеющих седловой точки (аналитический способ). 13. Решение платежных матриц 2*2 не имеющих седловой точки (графический способ). 14. Понятие о теории статистических решений. 15. Априорная и апостериорная вероятность событий. 16. Расчет апостериорной вероятности. 17. Расчет целесообразность местного поиска. Матрицы добычи и сожалений. 18. Расчет целесообразности местного поиска. Выбор лучшего способа действия по величине рисков. 19. Расчет выгодности перехода из одного промыслового района в другой. Возможные варианты обстановки, расчет матрицы добычи. 20. Переход из одного промыслового района в другой. Использование матриц сожалений. 21. Системы массового обслуживания и их работа. 22. Показатели эффективности обслуживания. 23. Расчет характеристик систем обработки судов на промысле. 24. Обобщенные потери систем обработки. 25. Сущность сетевого планирования и управления. 26. Основы теории управления запасами. 27. Методы расчета расстояний по алгоритму Литтла. 28. Взаимозависимость между параметрами промысла. 29. Результаты применения методов оптимального управления на промысле. 30. Перспективы развития тактики промысла. Задача №1
1.Составить математическую модель оптимальной загрузки судна по своим числовым данным. 2. Решить задачу аналитически с учетом жестких ограничений полного использования грузоподъемности судна. Определить возможную величину фрахта при заданных значениях с1 и с2. 3. Выбрать масштаб графического построения и в прямоугольной системе координат q 1 и q2 построить область допустимых решений и направление целевой функции. 4. Определить оптимальную загрузку судна и выполнить полный анализ полученных результатов.
q1=3000-q2 0,5(3000-q2)+2q2=4500 1500-0,5q2+2q2=4500 1500+1,5q2=4500 1,5q2=3000 q2=2000т q1=3000-2000=1000 т При этом значение целевой функции будет следующим: L1 = S Ci*Xi = C1 * q1+ C2 * q2 = 8*1000+4*2000 = 16000 руб. Математическая модель задачи для двух грузов будет иметь вид: q1+q2 £Dч– ограничения по грузоподъемности u1q1+u2q2£W – ограничения по грузовместимости (по объему)
или
7) L=C1q1+C2q2Þmax (min) C1 и C2 – затраты по перевозке 1 т. груза при решении задачи на min; C1 и C2 – оценка фрахта тонны перевозимого груза при решении задач на max. 2. Для графического решения задачи выбираем масштаб построения и в прямоугольной системе координат q1 и q2 производятся следующие построения. Заменяем во всех ограничениях знаки неравенства на знаки равенства и в заданном масштабе строят линии соответствующие этим равенствам. qo1+ qo2 =3000 0,5qo1+2qo2 =4500 300 = W1 = 750 1800 = W2 = 4500 Затем строим эти прямые в декартовой системе и находим область, удовлетворяющую соответствующим неравенствам. Эта область и является Областью Допустимых Решений (ОДР), любая точка которой удовлетворяет условиям задачи. Целевую функцию L = S Ci*Xi = C1 * q1+ C2 * q2 приравниваем к любому положительному числу – в нашем случае: Lоптх =8 * q1+ 4 * q2 = 3000, и строим эту прямую. Потом перемещаем ее параллельно самой себе до прикосновения с самой отдаленной от начало построения точкой – в нашем случае это точка "А". Координаты этой точки "А" дают оптимальное решение qo1, qo2. Сняв значения qo1, qo2, анализируем полученный результат. Для этого находим значение целевой функции при полученных qo1, qo2:
qo1 = 750 т qo2 = 2063 т
L опт = S Ci*Xi = C1 * q1+ C2 * q2 = 8*750 +4*2063 =14252 руб. Как видно из полученного решения, L1, равное 16000 руб., больше чем Lопт, равное 14252 руб., на 1748 руб. Это означает, что загрузка судна по Lопт менее выгодна, так как грузовместимость используется полностью, а грузоподъемность еще остается в запасе, что и отражается на величине дохода. Определяющим ограничением в нашем случае является W1max = 750 м3. Если его исключить, то можно подобрать такое решение, при котором можно принять на борт такое сочетание груза q1 и q2, чтобы добиться оптимального использования грузовместимости и грузоподъемности.
3. Для расчетов составляем симплекс матрицу в которую записывается исходные ограничения в виде уравнений за счет введения в неравенства фиктивных переменных: y1, y2, y3, y4. y1+q1+q2=3000 y2+0,5q1+2q2=4500 y3+ 0,5q1=750 y4+ 2q2=4500 Показатели целевой функции записываются в симплекс матрицу со знаками (-) при условии В первой матрице по колонкам переменных записываем их коэффициенты в соответствующих уравнениях. Таблица 1
Таблица 2
Таблица 3
Оптимальной величиной фрахта является 18000 руб. при цене фрахта по первому грузу 8 руб. за 1 тонну по второму грузу 4 руб. за 1 тонну.
4. В ходе проведенного решения было установлено, что оптимальная цена фрахта судна 18000 руб. при цене фрахта по первому грузу 8 руб. за 1 тонну по второму грузу 4 руб. за 1 тонну. Это решение было получено аналитически(симплекс-методом). Проведенное графическое решение дало результат 14 252 руб. Графическое решение менее оптимальное в связи с тем что не полностью используется грузоподьемность судна. Задача № 2 Выбор оптимального промыслово-технологического режима работы судна. (Аналитическое решение)
А - суточная добыча, т K2 - коэффициент расхода сырья на 1 т. второго вида продукции. С1,С2,С3 - оптовая цена за 1 т. различного вида продукции. Составить математическую модель задачи выбора оптимального технологического режима траулера по своим данным с учетом возможностей выпуска различных видов продукции в объеме 40, 20 и 2 т. и коэффициентов расхода сырья на выпуск 1 т. Готовой продукции соответственно 1,0 К2, 2,0. Заполнить исходную симплекс-матрицу и выполнить необходимое число итераций для получения оптимального решения. Проанализировать полученное решение с учетом заданных условий и возможных изменений условий (изменение цен, увеличения или уменьшения вылова и т.д.). 1.Рассматриваем условия работы траулера по следующим показателям: Максимально-возможный вылов рыбы за сутки А=72 т 2) Условия работы: х1 – выпуск 1 вида продукции 40 т х2 – выпуск 2 вида продукции 20 т х3 – выпуск 3 вида продукции 2 т Коэффициент расхода сырья х1 – выпуск 1 вида продукции 1 х2 – выпуск 2 вида продукции 1,6 х3 – выпуск 3 вида продукции 2
4) стоимость 1 т готовой продукции х1 ® 400 40 т х2 ® 600 20 т х3 ® 1000 2 т таким образом, математическая модель задачи имеет вид: L=400X1+600X2 +1000X3→ max x1+1,6x2+2x3£72 - ограничение по вылову, x1+x2+x3£62 - ограничения по выпуску продукции, x1£40 - ограничения по выпуску 1 вида продукции, х2£20 - ограничения по выпуску 2 вида продукции, х3£2 - ограничения по выпуску 3 вида продукции, х1³0 х2³0 х3³0 - положительные значения показателей работы судна. 2. Для расчетов составляем симплекс матрицу, в которую записывается исходные ограничения в виде уравнений за счет введения в (виде уравнений) неравенства фиктивных переменных: у1, у2, у3, у4. у1+х1+1,7х2+2х3=72 у2+х1+х2+х3=62 у3+ х1=40 у4+ х2=20 у5+ х3=2 показатели целевой функции записываются в симплекс матрицу со знаками (-) при условии в первой матрице по колонкам переменных записываем их коэффициенты в соответствующих уравнениях. таблица 1
таблица 2
|

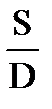

 .
. курс прицельного траления можно выбирать приведением ядра косяка на курсовой угол qc = 0. В этом случае еще до встречи с косяком трал успевает прийти к направлению диаметральной плоскости судна.
курс прицельного траления можно выбирать приведением ядра косяка на курсовой угол qc = 0. В этом случае еще до встречи с косяком трал успевает прийти к направлению диаметральной плоскости судна.
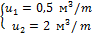
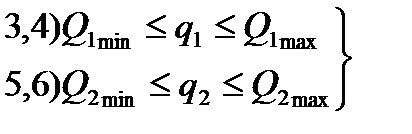 ограничение по количеству отдельных грузов
ограничение по количеству отдельных грузов ограничение по объему отдельных грузов
ограничение по объему отдельных грузов
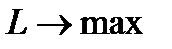 .
.


