
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коррекция системы автоматического управленияСодержание книги
Поиск на нашем сайте
Динамические показатели качества в значительной мере определяются инерционными свойствами звеньев САУ. К таким звеньям в рассматриваемом примере относятся ЭМУ, Г и Д, передаточные функции которых имеют довольно существенные значения основных постоянных времени. Точность работы САУ также зависит от возмущающих воздействий, действующих на объект управления и силовые преобразователи. К таковым в рассматриваемом следящем электроприводе можно отнести колебания напряжения промышленной сети, вследствие чего изменяется скорость приводных двигателей, и изменения моментов сопротивления на валу двигателя. Для уменьшения влияния инерционности и возмущений в САУ вводят местные обратные связи. Для расчета этих дополнительных контуров управления целесообразно использовать методику последовательной коррекции с подчиненным регулированием координат. В используемой в качестве примера САУ можно ввести два внутренних вложенных друг в друга контура регулирования: один по напряжению генератора, второй по скорости электродвигателя. Организация этих обратных связей представлена на рис. 7.1.
Рис. 7.1. Реализация подчиненного регулирования
В данной схеме регулятор напряжения РН и регулятор скорости РС помещены между ФЧВ и УПТ, т.к. коррекцию удобнее реализовать на постоянном токе в слаботочной части прямого канала управления. Здесь датчиком внутреннего контура является делитель напряжения, с которого часть напряжения
Расчет контура регулирования напряжения
Структурная схема первого внутреннего контура представлена на рис. 7.2. Здесь
Рис. 7.2. Структурная схема контура регулирования напряжения
В соответствии с методикой подчиненного регулирования координат внутренние контуры настраиваются по быстродействию на так называемый модульный оптимум, которому соответствует желаемая ПФ разомкнутой системы следующего вида
где В качестве
т.е. представляет собой колебательное звено с незначительным коэффициентом демпфирования Переходная характеристика такого контура для
Рис. 7.3. Переходная характеристика желаемой системы
Возьмем в качестве нескомпенсированной постоянной времени
Зададимся значением коэффициента передачи датчика напряжения
Теперь можно определить ПФ разомкнутого контура
После этого рассчитывается ПФ
В результате получим
где Поделив числитель ПФ
где
Анализ показывает, что РН реализует пропорционально - интегрально - дифференциальный (ПИД) закон управления.
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 249; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.48.5 (0.01 с.) |


 подается на вычитающий вход РН. В качестве датчика скорости используется тахогенератор ТГ (со своим делителем напряжения), напряжение с которого поступает на вычитающий вход РС. Далее рассматривается методика последовательной коррекции с подчиненным регулированием координат для синтеза РН и РС.
подается на вычитающий вход РН. В качестве датчика скорости используется тахогенератор ТГ (со своим делителем напряжения), напряжение с которого поступает на вычитающий вход РС. Далее рассматривается методика последовательной коррекции с подчиненным регулированием координат для синтеза РН и РС. - передаточная функция РН,
- передаточная функция РН, 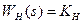 - ПФ делителя напряжения.
- ПФ делителя напряжения.
 ,
, – нескомпенсированная постоянная времени.
– нескомпенсированная постоянная времени. – ПФ реального интегратора. При этом желаемая ПФ замкнутой системы определяется соотношением
– ПФ реального интегратора. При этом желаемая ПФ замкнутой системы определяется соотношением ,
, .
.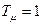 с приведена на рис. 7.3. Из нее видно, что перерегулирование
с приведена на рис. 7.3. Из нее видно, что перерегулирование  и длительность переходного процесса
и длительность переходного процесса  достаточно малы
достаточно малы  . Точность такого контура приемлема, т.к. он обладает астатизмом первого порядка (в канале управления имеется один интегратор).
. Точность такого контура приемлема, т.к. он обладает астатизмом первого порядка (в канале управления имеется один интегратор).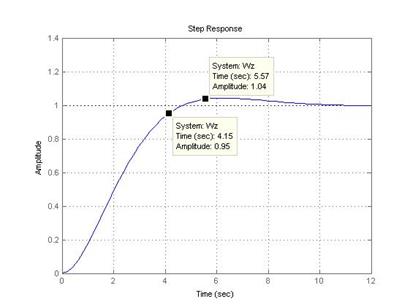
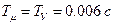 . Тогда желаемая ПФ разомкнутого контура будет иметь следующий вид:
. Тогда желаемая ПФ разомкнутого контура будет иметь следующий вид:
 , исходя из следующих соображений. Максимальное напряжение цепи обратной связи
, исходя из следующих соображений. Максимальное напряжение цепи обратной связи  , подаваемого на РН, ограничим значением
, подаваемого на РН, ограничим значением  при максимальном значении напряжения генератора
при максимальном значении напряжения генератора  . Отсюда получим
. Отсюда получим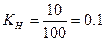 .
. :
: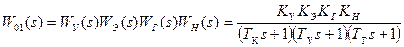 .
. по соотношению
по соотношению .
. ,
, с – постоянная времени интегрирования РН.
с – постоянная времени интегрирования РН. на ее знаменатель, получим параллельную структуру РН:
на ее знаменатель, получим параллельную структуру РН: ,
,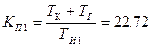 – коэффициент передачи пропорционального звена;
– коэффициент передачи пропорционального звена; с – коэффициент передачи дифференциатора.
с – коэффициент передачи дифференциатора.


