
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование исходной системыСодержание книги Поиск на нашем сайте
Анализ исходной САУ сводится к определению её точности, запаса устойчивости и быстродействия. Для решения этих задач необходимо в первую очередь получить ПФ разомкнутой системы W (s), которая равна произведению ПФ всех звеньев замкнутого контура регулирования. В частности, для структуры, приведенной на рис. 4.1, имеем:
или
где K = KС KВ KУ KЭ KГ KД KP =1.584 – коэффициент передачи разомкнутой системы. Передаточной функции разомкнутой системы соответствует tf-модель, получаемая перемножением tf-моделей передаточных функций всех звеньев замкнутого контура САУ. В рассматриваемом случае получим:
>> W=Wd*We*Wg*Wr*Wc*Wv*Wy
Transfer function: 1.584 ---------------------------------------------------------------------------------------- 2.88e-005 s^6 + 0.00529 s^5 + 0.08456 s^4 + 0.5012 s^3 + 1.206 s^2 + s Оценка точности исходной системы
Точность работы следящей системы необходимо оценивать ошибкой обработки входного воздействия
где
Пусть Ω м =17 град/с = 0.2967 рад/с, εм =15 град/с2 = 0.2618 рад/с2. Введем эти параметры в среду MatLab:
>> qm=0.2967 % ввод максимальной скорости qm = 0.2967
>> еm=0.2618 % ввод максимального ускорения еm = 0.2618 Определим амплитудное значение
>> Bm=(qm^2)/еm Bm = 0.3363
>> wk=еm/qm wk = 0.8824
Ошибка слежения определяется уравнением
где
где W(s) – ПФ разомкнутой системы. Для определения
>> Fe=feedback(1,W)
Transfer function: 2.88e-005 s^6 + 0.00529 s^5 + 0.08456 s^4 + 0.5012 s^3 + 1.206 s^2 + s -------------------------------------------------------------------------------------------------- 2.88e-005 s^6 + 0.00529 s^5 + 0.08456 s^4 + 0.5012 s^3 + 1.206 s^2 + s + 1.584
Учитывая, что при гармоническом входном воздействии
Для рассматриваемого примера получим следующее максимальное значение ошибки
>> Em=freqresp(Fe,wk)*Bm
Em = -0.1408 + 0.3706i
т.е. имеем комплексное значение рассогласования Для оценки амплитудного значения ошибки следует перейти к модульному соотношению для
В среде MatLab это осуществляется с помощью функции абсолютного значения abs:
>> Em=abs(Em)
Em = 0.3964
Полученное значение Определение запаса устойчивости исходной САУ Устойчивость замкнутой САУ удобнее всего оценивать по ПФ разомкнутой системы с помощью логарифмического критерия Найквиста. Для этого необходимо построить ЛХЧ разомкнутой системы. В Control System Toolbox для расчета ЛХЧ применяются две функции bode и mаrgin. Удобнее использовать последнюю, т.к. результатом её выполнения является не только графики ЛЧХ, но и численные значения запаса по фазе Рm, частоты среза Применим функцию mаrgin для исследования запаса устойчивости рассматриваемого варианта следящей системы:
>> margin (W); grid on
Здесь команда grid on использована для нанесения сетки на график. В результате получаются ЛЧХ, представленные на рис. 6.1. Из них видно, что система имеет очень малый запас по фазе
Рис. 6.1. ЛЧХ разомкнутой САУ
Следует отметить, что в удовлетворительно спроектированных системах запас по фазе лежит обычно в диапазоне
|
|||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 218; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.12.244 (0.009 с.) |



 ,
, , представленного в задании на проектирование максимальной скоростью
, представленного в задании на проектирование максимальной скоростью 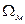 и максимальным ускорением
и максимальным ускорением  εм. По этим двум параметрам можно сформировать гармоническое входное воздействие
εм. По этим двум параметрам можно сформировать гармоническое входное воздействие ,
, – амплитудное значение
– амплитудное значение  – частота гармонического воздействия.
– частота гармонического воздействия. и частоту эквивалентного гармонического воздействия
и частоту эквивалентного гармонического воздействия  :
: ,
, – передаточная функция для ошибки
– передаточная функция для ошибки  по входному воздействию
по входному воздействию  :
: ,
, также изменяется гармонически, можно воспользоваться частотным методом оценки точности. Для определения значения частотной передаточной функции
также изменяется гармонически, можно воспользоваться частотным методом оценки точности. Для определения значения частотной передаточной функции 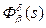 при
при  , удобнее всего воспользоваться функцией freqresp (Fe,wk).
, удобнее всего воспользоваться функцией freqresp (Fe,wk). :
: .
. и запаса по амплитуде Gm.
и запаса по амплитуде Gm. = Pm=13°, т.е. замкнутая САУ устойчива, но находится близко к границе устойчивости.
= Pm=13°, т.е. замкнутая САУ устойчива, но находится близко к границе устойчивости.



