
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модуль 2. Молекулярна фізика і термодинаміка. Електрика
Лабораторна робота № 5
ВИЗНАЧЕННЯ ВІДНОШЕННЯ ПИТОМИХ ТЕПЛОЄМНОСТЕЙ ГАЗІВ МЕТОДОМ АДІАБАТИЧНОГО РОЗШИРЕННЯ
Мета роботи: вивчити метод визначення відношення питомих теплоємностей повітря, визначити експериментально та теоретично числове значення відношення cp/c v, обчислити похибки вимірювання. Прилади та обладнання: балон об’ємом 20л, водяний диференційний манометр зі шкалою, насос.
Теоретичні відомості Питомою теплоємністю речовини називається фізична величина, що дорівнює кількості теплоти, яку необхідно надати одиниці маси речовини для підвищення її температури на 1K. Для газів ця величина залежить від умов, при яких проходить нагрівання – при сталому об’ємі чи при сталому тиску, і тому розрізняють відповідно питому теплоємність при сталому об’ємі c v та питому теплоємність при сталому тиску cp. Величини c v і cp мають різні значення для одного й того ж газу, оскільки кількість теплоти, надана газу при різних умовах, розподіляється по-різному. Згідно з першим принципом термодинаміки під час нагрівання при сталому об’ємі вся теплота витрачається тільки на збільшення внутрішньої енергії речовини, а під час нагрівання при сталому тиску підведена теплота витрачається на збільшення внутрішньої енергії газу та на виконання роботи проти зовнішніх сил. Безпосередньо виміряти cp і, особливо, c v важко, оскільки теплоємність газу становить мізерну долю теплоємності посудини, в якій міститься газ, тому вимірювання виконується неточно. Простіше виміряти відношення cp/c v, яке надасть величину показника адіабати – g. Величина cp/c v = g входить до рівняння Пуассона, яке описує адіабатичний процес зміни стану ідеального газу:
pVg = const. (1)
Співвідношення cp/c v = g залежить тільки від числа ступенів вільності руху молекул, які входять до складу газу:
де i – число ступенів вільності руху. Для одноатомного газу i =3, двохатомного i =5, трьохатомного та багатоатомного i =6.
Опис методу
Метод, який використовується в даній роботі був запропонований Клеманом і Дезормом. В його основі – використання адіабатичного розширення газу. Адіабатичним називається процес, який проходить без теплообміну з навколишнім середовищем. Перший принцип термодинаміки для адіабатичного процесу записується наступним чином:
A + DU = 0, або A = – DU,
де A – робота, виконана газом; DU – зміна внутрішньої енергії газу. З цієї формули видно, що робота по розширенню газу виконується за рахунок зміни внутрішньої енергії газу; температура газу при цьому знизиться. Під час же адіабатичного стискання газу його температура підвищиться. Якщо об’єм газу змінюється досить швидко, то внаслідок того, що теплопровідність газу невелика, процес можна розглядати як дуже близький до адіабатичного. Прослідкуємо за послідовністю процесів, що відбуваються у даному лабораторному експерименті та виведемо формулу для обчислення g.
У скляний балон (рис. 1) за допомогою насосу нагнітають повітря, створюючи всередині балону тиск, вищий за атмосферний. Цей стан відповідатиме початку експерименту (рис. 2, точка 1) і описується параметрами p 1, V 1, T 1. Швидке розширення газу можна вважати адіабатичним. Тому, відкриваючи кран на короткий час, протягом якого тиск всередині балону досягне атмосферного, можна вважати, що газ перейшов до нового стану, який характеризується параметрами p 2, V 2, T 2 < T 1 (рис. 2, точка 2). При цьому температура T 2 газу після адіабатичного розширення буде меншою від T 1. Параметри станів 1 та 2 зв’язані рівнянням адіабатичного процесу. Через 2-3 хвилини після перекривання крану газ у балоні нагрівається до температури навколишнього повітря T 1. Але оскільки під час цього нагрівання об’єм V 2 залишається незмінним, то тиск у балоні підвищується до значення p 3. Новий стан газу характеризується параметрами p 3, V 2, T 1 (рис. 2, точка 3). Порівнявши кінцевий стан газу (точка 3) з початковим (точка 1), бачимо, що вони знаходяться при однаковій температурі. Отже, за законом Бойля – Маріотта: p 3 V 2 = p 1 V 1. (2)
Виконаємо деякі перетворення в цьому рівнянні. Піднесемо його до степеня g і поділимо на рівняння (1):
Візьмемо натуральний логарифм від рівняння (3):
Умови експерименту надають змогу спростити розрахункову формулу. А саме, якщо позначити початковий тиск у балоні p 1, початкову різницю рівнів рідини в манометрі H, то:
p 1 = p 2 + bH, (5) де p 2 – атмосферний тиск; b – коефіцієнт переходу від різниці рівнів рідини до тиску. Для тиску p 3 різницю рівнів позначимо h, тоді:
p 3 = p 2 + bh. (6)
Визначивши p 3 = p 1 – b(H–h). (7)
Підставивши p 2 (з рівняння (5)) і p 3 (з рівняння (7)) у рівняння (4), знайдемо:
Величини
значень x, отримаємо:
Таким чином, формула (8) є робочою формулою для розрахунку g.
Порядок виконання роботи 1. Закрити трубку Б (див. рис. 1) і повільно нагнітати повітря в балон, доки різниця рівнів рідини в манометрі не стане дорівнювати (20-30)см. 2. Виміряти значення різниці рівнів рідини H в манометрі. 3. Відкрити трубку Б, випустити з балону надлишок повітря і знову закрити. Проміжок часу з моменту відкриття до моменту закриття повинен дорівнювати (1-2)с. 4. При закритій трубці Б почекати (2-3)хв. і потім виміряти нове значення різниці рівнів рідини h у манометрі. Якщо різниця рівнів рідини в манометрі при вимірах постійно зменшується, то потрібно вжити заходів для забезпечення герметичності системи. Простіше кажучи – перетиснути трубку А, щоб запобігти натіканню повітря через клапан насосу. 5. Експеримент повторити 5 разів, зберігаючи одне й теж саме значення H та вимірюючи кожний раз значення h. Результати вимірювань записати в таблицю 1. Таблиця 1
|
||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 555; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.154.150 (0.013 с.) |
 ,
, Рис. 1.
Рис. 1.
 Рис. 2.
Рис. 2.
 ®
® 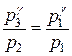 ®
®  ®
®  . (3)
. (3) ,
,  . (4)
. (4) з рівняння (5) і підставивши його в рівняння (6), отримаємо:
з рівняння (5) і підставивши його в рівняння (6), отримаємо: .
.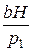 та
та  набагато менші за одиницю, тому, використавши наближену формулу ln(1– x)»– x, справедливу для малих
набагато менші за одиницю, тому, використавши наближену формулу ln(1– x)»– x, справедливу для малих . (8)
. (8)


