
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многокутники. Поняття площі фігури.Содержание книги
Поиск на нашем сайте
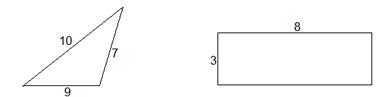
а) 5, 8, 7 см в) 3, 6, 10 см б) 10, 4, 6 см г) 6, 7, 7 см?
а) 3см і 12см б) 7см і 16см в) 2м 61см і 1м 12см.
а) його довжину збільшити на 6см б)довжину збільшити на 5см, а ширину зменшити на 7см в) довжину і ширину збільшити у три рази
б) А сам будинок стояв у куті двору і займав квадрат зі стороною 20 бумбамсів. Цар задумав покрити весь двір килимами, які мають форму прямокутника зі сторонами 2 і 3 бумбамса. Скільки потрібно для цього килимів?
Звичайні дроби.
1. Прочитайте: 1/7, 1/42, 1/355, 1/1001, 1/1000000.
2. Яка частина фігури замальована?
3. Яку частину року становить 1 місяць? 5 місяців? 8 місяців?
4. Яку частину м становить 1см; 5см; 10см; 20см?
5. Яку частину години становить урок?
6. Прочитай дроби, назві чисельник і знаменник кожного дробу і поясни, що вони означають: 7. Скільки г в
9. Клоун сказав, що його зріст 10. Поясніть рівність: 10 = 11. Дріб дорівнює своєму чисельнику. Чому дорівнює її знаменник?
12. Яку частину години становлять: 15хв; 20 хв; 10хв; 5хв; 1хв; 30хв; 40хв; 50хв; 25хв; 7хв; 35хв; 55хв; 13хв; 53хв.
13. Скільки хвилин становлять:
14. Як впізнати, який з 2-х дробів з однаковими знаменниками більше? Як впізнати, чи дріб більше за 1, чи менше за 1, чи дорівнює 1? Як називаються дроби менші за 1? А дроби більші за 1?
15. Порівняйте дроби:
16. Які з наступних дробів правильні, які неправильні:
17. При яких х дріб 18. При яких а дріб
19. Як зміниться дріб, якщо: а) його чисельник збільшити у 2 рази; б) його чисельник зменшити у 3 рази; в) його знаменник збільшити у 2 рази; г) його знаменник зменшити у 3 рази. 20. Знайди число, якщо а)
21. Назвіть одиницю у вигляді дробу зі знаменником: 8; 13; 71; 115.
22. При яких натуральних значеннях х дріб буде правильним: а) 23. Знайди х: 24. Знайди цілу і дробову частину неправильного дробу:
25. Прочитайте мішані числа:
26. Між якими послідовними натуральними числами знаходиться мішане число:
27. Порівняйте числа: а) г) 28. Знайти значення числового виразу: а) б) в) г)
29. Розв’яжіть рівняння: а) б) в)
30. Назвіть неправильний дріб, який дорівнює мішаному числу: а)
32. Знайди різницю: а) 33. Розв’яжіть рівняння: а) 34. Сума числа і його чверті дорівнює 20. Знайти це число. 35. При якому значенні у рівні дроби:
Десяткові дроби
1. Назвіть найстарший і наймолодший розряди у кожного з чисел: 65,18; 9,03; 4,0404; 7,01; 7,001; 7,0001; 6,0277.
2. Прочитайте числа: 3,1415; 31,415; 0,31415; 3,14150; 0,314150; 3,01415; 3,01040105.
3. Обчисліть результат і назвіть десятковим дробом: а) 70 +7 + б) 80+ в)
4. Замініть * цифрою:
5. Крохмаль становить 0,2 ваги картоплі. Скільки знадобиться картоплі для отримання 400г крохмалю?
6. Порівняйте числа: 6,31 і 17,28 0,0302 і 0,0032 0,5 і 0,49 6,837 і 6,829 0,025 і 0,035 0,4607 і 0,4617 43,24 і 43,172 5,025 і 5,03 6,001 і 6,01 0,527 і 0,572 16,2302 і 12,23 1,82 і 18,2
7. Яке натуральне число стоїть між числами: 18 і 20; 7,3 і 8,5; 33 і 34,3; 99,9 і 101; 0,23 і 1,7.
8. Між якими сусідніми натуральними числами стоїть число: 8,4; 16,376; 99,5; 83,17; 100,001.
9. Який знак треба поставити між цифрами 3 і 4, щоб одержати число, яке більше 3, але менше за 4.
11. Прочитай дроби: 0,7; 0,70; 0,700; 0,7000; 0,70000. Що можна сказати про ці дроби?
12. До якого розряду округлені числа: а) 15,357 ≈ 15,36 г) 10,5601 ≈ 10,560 б) 15,357 ≈ 15,4 д) 10,5601 ≈ 10,6 в) 15,357 ≈ 15 е) 10,5601 ≈ 10
13. Яка з точок лежить правіше на числовому промені? А(3,5) чи В(3,4) Е(1,99) чи Н(2) К(0) чи Х(0,0001) С(7,92) чи У(7,89) М(5,009) чи N(5.01) Q(0,001) чи Р(0,0001)?
14. Дивлячись на рівність 20,6 + 3,7 = 24,3, назвіть, не обчислюючи, чому дорівнює різниця: 24,3 – 3,7?
15. Виконайте дії: 3,7 + 1,1 7,55 + 2,46 10 – 0,25 1,42 + 0,33 0,033 + 0,167 6,2 – 2,3 1,42 + 3,3 6,9 – 2,3 2,37 – 0,64 7,53 + 2,46 2,87 – 0,64 68,3 – 23,8 0,98 + 0,02 68,3 – 23,3 10 – 7,77 3,7 + 1,7 0,84 – 0,52 0,84 – 0,25.
16. Знайти суму: 7,8 + 0,1 0,25 + 0,1 0 + 0,57 7,8 + 0,2 0,25 + 0,01 23,629 + 0 7,8 + 0,7 0,25 + 0,001 3,456 + 1
17. Поставити правильно коми: 32 + 18 = 5 42 + 17 = 212 63 – 27 = 603 3 + 108 = 408 736 – 336 = 4 57 – 4 = 17
18. Обчислити: 3,249 ∙ 10 85,72 ∙ 0,1 2,5: 10 0,12 ∙ 100 5,13 ∙ 0,01 137,258: 100 0,1 ∙ 1000 725,3 ∙ 0,001 10,25: 1000 328,697 ∙ 10000
19. Обчислити: 0,3 ∙ 8 9 ∙ 0,7 0,4 ∙ 0,6 0,42 1,4 ∙ 2 11 ∙ 0,6 0,12 ∙ 0,4 0,32 1,7 ∙ 3 5 ∙ 0,14 1,7 ∙ 0,3 0,112 0,13 ∙ 4 60 ∙ 0,5 1,9 ∙ 0,6 0,13
20. Знайти значення виразу, виконуючи обчислення найбільш зручним способом: (19,3 ∙ 5) ∙ 20 57,48 ∙ 0,396 + 42,52 ∙ 0,396 2,5 ∙ 1,47 ∙ 4 0,89 ∙5,06 + 5,06 ∙ 1,11 0,2 ∙ 3,87 ∙ 0,5 53,76 ∙ 78,91 – 43,78 ∙ 78,91 0,25 ∙ 7,53 ∙ 0,4 8,39 ∙ 4,32 – 4,32 ∙ 6,39
21. Знайти 0,1 від 15,2; 0,01 від 132; 0,2 від 32.
22. Виконати ділення: 2,6: 2 3,6: 4 5,68: 8 6,06: 6 15,9: 3 5,4: 9 1,05: 5 60,6: 6 20,8: 4 0,18: 6 4,26:6 11,11: 11 18,9: 9 0,24: 3 0,032: 4 111,1:11
23. Використовуючи властивості множення і ділення, обчислити: (7,7 ∙ 6): 7 (17: 25): 4 (8,8 ∙ 9):11 (7,9: 5): 2
24. Дивлячись на рівність 1,57 ∙ 1,2 = 1,884, скажіть, не обчислюючи, чому дорівнює частка 1,884: 1,2?
25. Знайти частку: 0,83: 0,1 3,456: 0,01 2,318: 0,001 0,1: 0,01 0,057: 0,1 0,17: 0,01 0,53: 0,001 0,01: 0,1
26. До якого розряду округлені числа: 2318,57 ≈ 2318,6 2318,57 ≈ 2320 2318,57 ≈ 2000 763,248 ≈ 800 763,248 ≈ 763 763,248 ≈ 763,25
Відсотки. 1. Як перетворити десятковий дріб у відсоток?
2. Як перевести відсоток у десятковий дріб?
3. Перетворити у десятковий дріб: 25%, 49%, 7%, 0,5%, 121%, 17,1%, 351,3%, 38%, 92%, 4%, 1%, 215%.
4. Перетворити у відсотки: 0,23; 0,98; 0,005; 0,716; 0,032; 1,92; 2,572; 0,35; 0,84; 0,01; 0,621; 0,071; 1,37.
5. На скільки відсотків 32 менше ніж 40? На скільки відсотків 40 більше 32?
6. Знайти: 0,01 від 725 0,25 від 100 7. Знайти число, якщо:
8. Знайти відсоток від числа: 1% від 100 10% від 50 50% від 50 20% від 200 25% від 40 110% від 200.
9. Знайти число, якщо: 80% його дорівнює 10 25% його дорівнює 5 50% його дорівнює 63 10% його дорівнює 40.
10. Вінні Пух взимку схуднув на 10%, але влітку знов поправився на 10%. Коли він був важчим: цієї осені, чи минулої?
Практичні обчислення.
8 і 10; 20 і 11; 6, 7 і 8; 19, 12 і 15; 5, 21, 11, і 23; 14, 33, 9 і 25; 10, 11, 12, 13 і 14; 19, 10, 7, 6, і 2.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 373; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.87.113 (0.011 с.) |




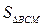 б)
б) 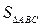 в)
в) 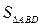 г)
г) 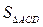



 Скільки кг в
Скільки кг в 



 і сказав, що в буфеті продається морозиво порціями по
і сказав, що в буфеті продається морозиво порціями по  . Усі сміялися, адже усім відомо, що тривалість антракту звичайно вимірюють у хвилинах, а масу порції морозива – у грамах. Скажіть, на скільки хвилин був об’явлений антракт і скільки г в одній порції морозива?
. Усі сміялися, адже усім відомо, що тривалість антракту звичайно вимірюють у хвилинах, а масу порції морозива – у грамах. Скажіть, на скільки хвилин був об’явлений антракт і скільки г в одній порції морозива?
 а маса
а маса  Усі сміялися, так як бачили, що клоун вибрав невдалі одиниці довжини і маси. Назвіть зріст клоуна у см і його масу у кг.
Усі сміялися, так як бачили, що клоун вибрав невдалі одиниці довжини і маси. Назвіть зріст клоуна у см і його масу у кг. 14 =
14 = 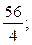
 ;
;  ; 13: 10 =
; 13: 10 = 
 від 1 год;
від 1 год; 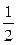 від 30 хв;
від 30 хв;  від 1 год;
від 1 год;  доби;
доби;  тижня?
тижня?





 менших від дробу
менших від дробу 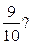
 більший за дріб
більший за дріб  , але менший
, але менший  ?
?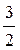 його дорівнює 9; б)
його дорівнює 9; б)  дорівнюють 10; в)
дорівнюють 10; в)  його дорівнюють 21.
його дорівнюють 21. б)
б)  в)
в)  г)
г) 


















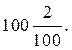
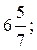



 б)
б)  в)
в) 
 д)
д) 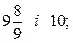 е)
е) 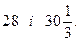
 д)
д) 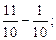 з)
з) 
 е)
е) 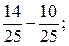 і)
і) 
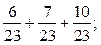 є)
є)  и)
и) 
 ж)
ж)  ї)
ї) 
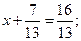 г)
г) 
 д)
д) 
 е)
е) 
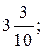 в)
в)  г)
г)  д)
д) 
 тижня, у другому – на
тижня, у другому – на  тижня менше. Скільки усього тижнів гастролював клоун? Скільки днів він провів у кожному місті?
тижня менше. Скільки усього тижнів гастролював клоун? Скільки днів він провів у кожному місті?
 б)
б)  в)
в)  г)
г) 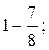 д)
д)  е)
е)  є)
є)  ж)
ж) 
 б)
б)  в)
в)  г)
г)  д)
д) 
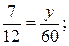
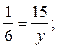

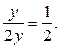
 г) 5 +
г) 5 +  ж)
ж) 
 д) 40 +
д) 40 +  з)
з) 
 е)
е)  і)
і) 

 від 123
від 123 його дорівнює 25; 0,01 його дорівнює 0,2.
його дорівнює 25; 0,01 його дорівнює 0,2.


