
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Побудова математичної моделі прогнозу необхідної кількості сировиниСодержание книги
Поиск на нашем сайте
Розглянемо більш докладно модель сезонної хвилі, побудованої на основі гармонійного аналізу. Нехай Функцію y(t) у досліджуваному інтервалі часу можна при виконання деяких умов представити нескінченним рядом синусоїдальних і косінусоідальних функцій (ряд Фур'є), наприклад, якщо функція кусочно-монотонна й обмежена (умови Дирихлє). Перша гармоніка має період, рівний довжині досліджуваного періоду. Друга гармоніка має період, рівний половині основного, третя – однієї третини основного і т.д. Узагалі якщо є р спостережень, то число гармонік не буде перевищувати Записуємо y(t) у вигляді суми
Коефіцієнти Аi, Bi та а0 оцінюються за методом найменших квадратів:
Одержання формул для коефіцієнтів полегшується завдяки властивості ортогональності:
Подібної ж рівності мають місце, якщо обидва члени замінені косинусами, якщо один член замінений косинусом, то сума в лівій частині (1.5) дорівнює 0. Позначимо:
Оцінки параметрів Ai, Bi та a0 знаходиться із системи рівнянь (1.6):
Оцінки параметрів Ai, Bi та a0 мають вигляд:
a0 = Ai = Bi =
якщо При Після цього, знайдені оцінки (1.7), (1.8), (1.9) підставляємо в (1.3) та використовуємо вираження y(t) для прогнозу. Наприклад, прогноз на момент t=p+1 дорівнює: Y(p+1)=a0+ Модель сезонної хвилі на основі гармонійного аналізу можна використовувати не тільки для короткострокового прогнозування, але і для довгострокового (наприклад, на квартал, рік і т.д.). Алгоритм методу простий в обчислювальному відношенні: по заданому тимчасовому ряді варто лише розрахувати оцінки параметрів Ai, Bi та a0, моделі сезонної хвилі (1.3). Прогнозування необхідного обсягу сировини, з використанням розробленої математичної моделі Розглянемо приклад. Задані числові дані об’єму сировини, які були взяті у поточному періоді. Потрібно спрогнозувати необхідний об’єм сировини та максимальну похибку прогнозу.
Як часовий ряд візьмемо об’єм сировини за 2009 р. по місяцях (таблиця 1.1). Таблиця 1.1 – Обсяги сировини, що споживалася по місяцях у 2009 р., млн. т.
Для того, щоб оцінити точність прогнозу, складеного на основі гармонійного аналізу, для побудови моделі використовуємо значення, складемо прогноз і порівняємо з реальними даними. Довжина часового ряду буде дорівнює 12, кількість гармонік візьмемо 3. Обчислимо значення а0 за формулою (7):
а0 = =6,642 Далі згідно формул (8) та (9) обчислимо значення коефіцієнтів
Одержані данні занесемо до таблиці 1.2 Таблиця 1.2 – Значення коефіцієнтів моделі сезонної хвилі з 3-а гармоніками
Визначимо значення ряду за формулою (1.3):
y(1)=6,642 + y(2)=6,642+ y(3)=6,642+ і так далі до y(12). У таблиці 1.3 приводяться значення згладженого ряду і відхилення від фактичних даних. Таблиця 1.3 – Порівняння розрахункових значень по моделі сезонної хвилі з 3-а гармоніками і фактичними значеннями за даними 2009 року
Середня помилка становить 10,8%, при складанні прогнозу з використанням 3-ох гармонік. Якщо ми отримаємо відхилення з більшим значенням чим 20% то потрібно брати більше гармонік та повторити обчислення, які були описані вище. За даними таблиці 1.3 будуємо графік зображений на рис. 1.1.
Рисунок 1.1 Графік зміни фактичних вихідних даних та розрахованих (прогнозних) даних на 12 місяців 2009 року.
Тепер визначимо прогнозовану величину майбутньої потреби сировини:
y(13)=6,642+ Тобто, на прогнозний місяць підприємству для надійного функціонування необхідно закупити 7,453 млн.т. вихідної сировини. Не дивлячись на те, що при розрахунку можлива помилка складає 10,8%, вона в подальших розрахунках не враховується, оскільки невідомо в більшу чи меншу сторону буде відхилення. Отже одержана величина фактично відповідає середній кількості сировини необхідної для роботи.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 326; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.253.53 (0.009 с.) |

 - тимчасовий ряд, що описує зміни показника yt «коливального характеру», t=
- тимчасовий ряд, що описує зміни показника yt «коливального характеру», t=  . Крім того, нехай y(t) – передбачувана теоретична залежність, що відповідає експериментальній.
. Крім того, нехай y(t) – передбачувана теоретична залежність, що відповідає експериментальній. . Для функції «коливального характеру» як правило їх потрібно визначити менше, також функції добре описуються декількома першими гармоніками.
. Для функції «коливального характеру» як правило їх потрібно визначити менше, також функції добре описуються декількома першими гармоніками. (1.3)
(1.3) (1.4)
(1.4) (1.5)
(1.5)
 j=
j=  .
. , (1.7)
, (1.7) , (1.8)
, (1.8) , (1.9)
, (1.9) .
. , А
, А  =0, У
=0, У  .
. (1.10)
(1.10)
 ,
,  :
: =
=  =0,289
=0,289 =
=  =0,239
=0,239 =
=  =0,069
=0,069 =
=  =0,233
=0,233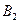 =
=  = 0,378
= 0,378 =
=  = -0,071
= -0,071 = 7,453
= 7,453 =7,098
=7,098 =6,485
=6,485
 =7,453млн.т.
=7,453млн.т.


