
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механические характеристики материалов. Их определение.Содержание книги
Поиск на нашем сайте
Свойства материалов при расчетах на прочность, жесткость и устойчивость определяются механическими характеристиками. Механические характеристики материалов можно определить нагружая образцы, до разрушения или значительной деформации, при любом виде нагружения. Наибольшее распространение имеют испытания на растяжение. На специальных машинах растягивают образцы, размеры которых ограничены стандартом, записывая автоматически зависимость изменения растягивающей силы F от удлинения образца Δℓ, т.е. диаграмму растяжения в координатах F = f(Δℓ). Эту диаграмму называют диаграммой растяжения или условной диаграммой растяжения. σpr - предел пропорциональности - наибольшее напряжение, до которого материал следует закону Гука Упругие свойства материала сохраняются до напряжения, называемого пределом упругости σe, т.е это наибольшее напряжение, до которого материал не получает остаточных деформаций. σy - предел текучести - напряжение, при котором происходит рост деформации без заметного увеличения нагрузки. В тех случаях, когда на диаграмме отсутствует явно выраженная площадка текучести, за предел текучести условно принимается величина напряжения, при котором остаточная деформация составляет 0,2.Точка D – предел прочности, максимальное напряжение, которое выдерживает материал не разрушаясь.
22. Понятие о твердости материалов Твердость (Н)– способность материала оказывать сопротивление проникновению в него инородного тела. Метод Бринелля (НВ) основан на вдавливании в поверхность испытуемого материала стального закаленного шарика диаметром 2,5; 5 или 10 мм под действием силы F, приложенной перпендикулярно к поверхности изделия в течение определенного времени. HB=F/S. (кгс/мм2). Твердость по Бринеллю при условиях испытания, когда диаметр шарика 10 мм, F = 3000 кгс и продолжительность выдержки под нагрузкой от 10 до 15 с, обозначается цифрами, характеризующими число твердости, и буквами НВ. Например, 120НВ, где 120 – число твердости в кгс/мм2; НВ – твердость по Бринеллю. Достоинства: Достаточная быстрота испытания, простота и надежность прибора, отсутствие необходимости тщательной подготовки поверхности. Недостатки: ограничение НВ <450, нельзя измерить твердость пленок, твердость деталей после химико-термической обработки из-за незначительной толщины обработанного поверхностного поля О твердости по методу Роквелла (HR) судят по разности глубин, на которые проникает алмазный конус с углом при вершине 120° или стальной закаленный шарик диаметром 1,588 мм при действии двух последовательно приложенных нагрузок: предварительной величиной 10 кгс и общей – 60, 100 или 150 кгс, равной сумме предварительной и основной нагрузок. Для определения числа твердости применяют три шкалы. Шкала В соответствует вдавливанию шарика и число твердости при этом обозначается HRB. Для более твердых материалов применяются шкалы А и Сэ, соответствующие вдавливанию алмазного конуса. Вначале индентор вдавливается в поверхность образца под предварительной нагрузкой, которая не снимается до конца испытаний, что обеспечивает точность измерений. Затем подается основная нагрузка (для шкалы А – 50 кгс, для шкалы В – 90 кгс, для шкалы С – 140 кгс), после снятия которой число твердости определяют глубиной отпечатка. Достоинства: совмещение операций вдавливания индентора и измерения размеров отпечатка, универсальности, небольшому размеру отпечатка. Недостатки: подготовка поверхности, условный и безразмерный численный результат. HR <170/ 1 HRC ≈ 10 НВ. Метод измерения твердости по Виккерсу (HV) заключается во вдавливании в испытываемый материал правильный четырехгранной алмазной пирамиды с углом в 136° между противоположными гранями. Число твердости по Виккерсу вычисляется путем деления нагрузки на площадь поверхности пирамидального отпечатка HV=F/S. Достоинства: алмазный индентор, сам отпечаток, размерность 1 HV ≈ 1 НВ Недостатки: не разрушающий быстро, ε0,2=кнв и εв=к1нв1 к=0,345 для конструкционных углеродистых сталей. 23. Понятие допускаемых напряжений. Условия прочности и жесткости конструкций. Условия прочности и жесткости конструкций - собственно условия прочности, максимальное напряжение конструкций σmax ≤ σadm Допускаемыми называют напряжения, соответствующие деформациям, допустимым при работе механизма. σadm = σпред/n; n>1,0 (σu, σв) для пластинных материалов → σпред = σу(σ0,2). n – коэффициент запаса прочности, представляемый в виде произведения n = n1n2n3…, который всегда больше единицы. Чем больше коэффициент запаса прочности, тем надежнее деталь в работе, но превышение n определенной величины ведет к чрезмерному увеличению габаритов и веса, что экономически невыгодно. Для пластичных материалов принимают n ≈ 1,4 … 1,6, для хрупких – 2,5 … 3,0. Условием прочности при растяжении (сжатии) будет выражение σ = F/ S ≤ σ0,2/ n =σadm. Проверить прочность нагруженного стержня, т.е. по заданной нагрузке и размерам поперечного сечения определить действительные напряжения и сравнить их с допускаемыми. Определить размеры поперечного сечения стержня по известной нагрузке и допускаемому напряжению материала S ≥ F/ σadm. Определить допускаемую продольную силу по заданным размерам S поперечного сечения стержня и допускаемому напряжению материала стержня F ≤ S·σadm. Далее, зная связь между продольной силой N и внешними силами F, можно найти предельную внешнюю нагрузку Fu. Выбрать материал нагруженного стержня по заданным размерам А поперечного сечения стержня и нагрузке, приняв или рассчитав величину коэффициента запаса прочности n: σ0,2 = n· σadm ≥ (n F) / S. 24. Деформация сдвига стержней При простом растяжении две части стержня, разделенные наклонным сечением, стремятся не только оторваться, но и сдвинуться одна относительно другой. Сдвигу противодействуют касательные напряжения, действующие в плоскости сечения. Если нормальные напряжения вызывают линейные деформации (удлинения и укорочения), то касательные напряжения вызывают угловые деформации γ, так называемые углы сдвига. Чистым сдвигом называют такоенапряженное состояние, когда по граням элемента в виде бесконечно малого кубика действуют только касательные напряжения. Например, чистый сдвиг наблюдается во всех точках скручиваемого стержня с круглым поперечным сечением. для большинства материалов до определенных величин нагружения имеется линейная зависимость между напряжениями и деформациями при сдвиге, которую выражает закон Гука:τ = G·γ, где G – модуль упругости материала при сдвиге Так как разрушение детали при деформации сдвига называют срезом, расчет на прочность при данной деформации называют расчетом на сдвиг или на срез. Примером соединений, рассчитываемых на срез, являются заклепочные, болтовые, сварные, паяные, клеевые соединения. Условие прочности при сдвиге имеет вид τ = Q/A ≤ τadm, где Q – равнодействующая внутренних сил в плоскости сдвига; А – площадь сдвига; τadm – допускаемое касательное напряжение материала детали.
25.Моменты инерции плоских сечений (прямоугольника, круга).
, где ρ – расстояние от площадки dA до полюса (точки 0).(1) Осевым моментом инерции сечения называется взятая по всей площади сечения сумма произведений площадей элементарных площадок на квадрат их расстояния до оси. Так, моменты инерции сечения относительно координатных осей z и y будут соответственно равны
момент инерции прямоугольника (2) с основанием b и высотой h относительно оси z, проходящей через центр масс параллельно основанию. За элементарную площадку dA примем площадь бесконечно тонкого слоя dA = bdy. Тогда
. Найдем моменты инерции круга относительно координатных осей y, z, проходящих через центр масс С. Так как оси являются диаметром круга, то Iy = Iz. Поэтому Iρ =2 Iy = 2 Iz, откуда Iy = Iz = Iρ/2 ≈ 0,05 d4.
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 631; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.009 с.) |

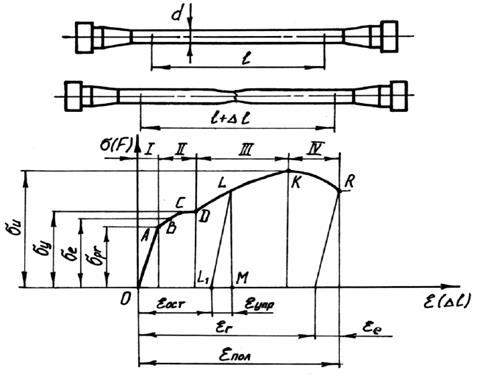
 Максимальные нагрузки → называются пределом прочности σв (σu) до точки K. относительное остаточное удлинение при разрыве
Максимальные нагрузки → называются пределом прочности σв (σu) до точки K. относительное остаточное удлинение при разрыве  и относительное остаточное сужение при разрыве
и относительное остаточное сужение при разрыве  , где ℓp, Ap – соответственно расчетная длина образца и площадь поперечного сечения в наиболее тонком месте шейки после разрыва. Противоположным свойству пластичности является хрупкость, т.е. способность материала разрушаться при незначительных остаточных деформациях.
, где ℓp, Ap – соответственно расчетная длина образца и площадь поперечного сечения в наиболее тонком месте шейки после разрыва. Противоположным свойству пластичности является хрупкость, т.е. способность материала разрушаться при незначительных остаточных деформациях.
 Полярным моментом инерции сечения называется взятая по всей площади сечения сумма произведений площадей элементарных площадок на квадрат их расстояния до данного полюса (точки).
Полярным моментом инерции сечения называется взятая по всей площади сечения сумма произведений площадей элементарных площадок на квадрат их расстояния до данного полюса (точки).
 Так как ρ2 = z2 + y2, сравнив выражения получим Iρ = Iz + Iy, т.е. сумма осевых моментов инерции сечения относительно двух взаимно перпендикулярных осей равна полярному моменту инерции этого сечения относительно точки пересечения рассматриваемых осей.
Так как ρ2 = z2 + y2, сравнив выражения получим Iρ = Iz + Iy, т.е. сумма осевых моментов инерции сечения относительно двух взаимно перпендикулярных осей равна полярному моменту инерции этого сечения относительно точки пересечения рассматриваемых осей.
 . Аналогично получим Iy = hb3/12.
. Аналогично получим Iy = hb3/12. Рассмотрим круг (3). За элементарную площадку dA примем площадь бесконечно тонкого кольца толщиной dρ: dA = 2πρdρ. Тогда
Рассмотрим круг (3). За элементарную площадку dA примем площадь бесконечно тонкого кольца толщиной dρ: dA = 2πρdρ. Тогда


