
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ динамики числа пожаров в городе за последние 5 лет
При анализе динамики числа пожаров в городе за последние 5 лет необходимо: · определить показатели изменения уровней временного ряда числа пожаров за анализируемый период; · выявить основную тенденцию ряда динамики, которая позволяет представить его изменение за анализируемый период в виде некоторой математической модели; · получить прогнозную оценку числа пожаров в городе на следующий год. l. Если исследованию подвергаются изменения определенной характеристики y со временем, то перечень значений этой характеристики в последовательные моменты или интервалы времени образует так называемый ряд динамики или временной ряд (соответственно различают моментные и интервальные временные ряды). Временные ряды могут быть образованы значениями абсолютных или относительных характеристик, либо значениями средних величин. 2. Значения изучаемой характеристики 3. При анализе временных рядов используют комплекс специальных показателей, характеризующих изменчивость в уровнях ряда. К таким показателям относится абсолютный прирост, коэффициент (или темп) роста, коэффициент (или темп) прироста. Расчет этих показателей производится для каждого 4. Абсолютный прирост
В качестве базы для сравнения можно принять предшествующий, начальный или средний уровни ряда. Значения абсолютного прироста 5. Коэффициент роста
В зависимости от соотношений значений рассматриваемого и базового уровней значение коэффициента роста
6. Коэффициент прироста
Значения Коэффициент прироста, выраженный в процентах, называется темпом прироста. Он показывает, на сколько процентов увеличилось или уменьшилось значение рассматриваемого уровня ряда 7. В качестве примера в табл. 10 представлены результаты расчета рассмотренных показателей для интервального временного ряда, отражающего динамику числа пожаров в городе за пять лет (N = 5). За базу для сравнения с тем или иным уровнем ряда
Таблица 10 Показатели ряда динамики числа пожаров в городе за 5 лет
Абсолютный прирост: Аt=yt-yбаз 2. Аt=246-252=6 3. Аt=288-246=42 4. Аt=300-288=12 5. Аt==326-300=26
Коэффициент роста Нt=yt/yбаз 2. Нt=246/252=0,976 3. Нt=288/246=1,170 4. Нt=300/288=1,042 5. Нt=326/300=1,087
Коэффициент прироста Вt=At/yбаз 2. Вt=-6/252=-0,023 3. Вt=42/246=0,17 4. Вt=12/288=0,042 5. Вt=26/300=0,087
8. При анализе временных рядов используются также следующие обобщенные показатели: средний уровень ряда, вычисление которого производится по формуле:
дисперсия ряда, по значению которой можно оценить разброс значений уровней ряда вокруг их среднего уровня, вычисляется по формуле: арстве; (5) стандарт ряда (среднеквадратичное отклонение), вычисляемый как
коэффициент вариации ряда, который является относительной мерой рассеяния значений уровней ряда вокруг их среднего уровня и вычисляется по формуле:
9. Для временного ряда, представленного в табл. 10, значения перечисленных обобщенных показателей оказались следующими:
10. Эффективным способом выявления основной тенденции процесса изменения уровней временного ряда является его математическое моделирование. При этом уровни ряда выражаются в виде функции времени . 11. Если характер динамики подтверждает предположение о том, что наблюдаемое в t -м году число пожаров в городе
где
12. Для нахождения неизвестных коэффициентов используется метод наименьших квадратов. Согласно этому методу, коэффициенты уравнения (9) вычисляются таким образом, чтобы сумма квадратов отклонений наблюдаемых значений
Чтобы найти неизвестные коэффициенты а и b, следует воспользоваться тем фактом, что в точке экстремума (в данном случае в точке минимума) производная функции равна нулю. Для этого нужно приравнять нулю частные производные:
что дает для определения коэффициентов а и b систему линейных уравнений
Решая эту систему, получаем уравнения для нахождения коэффици ентов а и b :
Зная величины коэффициентов а и b и предполагая, что имеющаяся тенденция изменения числа пожаров в городе останется неизменной, можно вычислить прогнозную оценку числа пожаров в интересующем году, подставив в уравнение (9) номер этого года.
13. В качестве примера, выполним прогнозирование числа пожаров в городе на год вперед по вышеуказанным исходным данным числа пожаров в городе за последние 5 лет. Для выявления тенденции изменения числа пожаров в городе используем аналитическое выравнивание временного ряда в виде зависимости (9). Для нахождения коэффициентов а и b воспользуемся формулами (14) и (15), предварительно составив вспомогательную табл. 11. Таблица 11 Вспомогательная таблица для вычисления коэффициентов а и b
Подставляя числовые значения из итоговой строки табл. 11 в уравнения (15) и (14), находим значения коэффициентов:
Используя уравнение (9), определяем ориентировочное значение числа пожаров в городе в следующем году (t = 6):
14. Наносим на график эмпирические значения числа пожаров за прошедшие 5 лет, выровненные уровни этого временного ряда и прогнозируемое значение для шестого года (рис. 1). 15. По результатам расчетов делаем вывод. Для рассматриваемого примера можно констатировать, что, несмотря на ежегодные колебания цепных показателей изменчивости временного ряда, наблюдается тенденция роста числа пожаров в городе. Этот факт необходимо будет учесть при обосновании требуемого количества сил и средств ПП города на перспективу.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 352; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.30.253 (0.02 с.) |
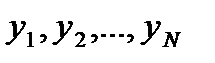 , образующие временной ряд, называют уровнями временного ряда. Первое
, образующие временной ряд, называют уровнями временного ряда. Первое 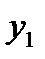 и последнее
и последнее 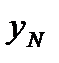 из этих значений соответственно называют начальным и конечным уровнями ряда.
из этих значений соответственно называют начальным и конечным уровнями ряда.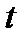 - го момента или интервала времени (t = 1, 2,..., N, где N -число анализируемых моментов или интервалов времени), которому соответствует эмпирическое значение изучаемой характеристики
- го момента или интервала времени (t = 1, 2,..., N, где N -число анализируемых моментов или интервалов времени), которому соответствует эмпирическое значение изучаемой характеристики 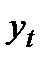 .
. показывает на сколько единиц увеличился или уменьшился рассматриваемый уровень ряда
показывает на сколько единиц увеличился или уменьшился рассматриваемый уровень ряда 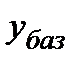
 (1)
(1)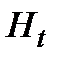 определяется как отношение рассматриваемого уровня ряда
определяется как отношение рассматриваемого уровня ряда 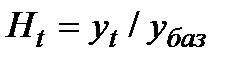 (2)
(2)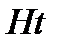 , может оказаться меньше единицы (при
, может оказаться меньше единицы (при 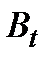 определяется как отношение абсолютного прироста
определяется как отношение абсолютного прироста 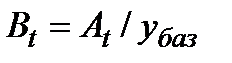 . (3)
. (3)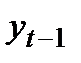 ). Вычисляемые при таком условии показатели
). Вычисляемые при таком условии показатели  ; (4)
; (4) ; (6)
; (6)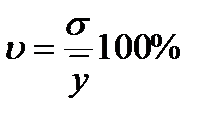 . (7)
. (7) пожаров/год;
пожаров/год;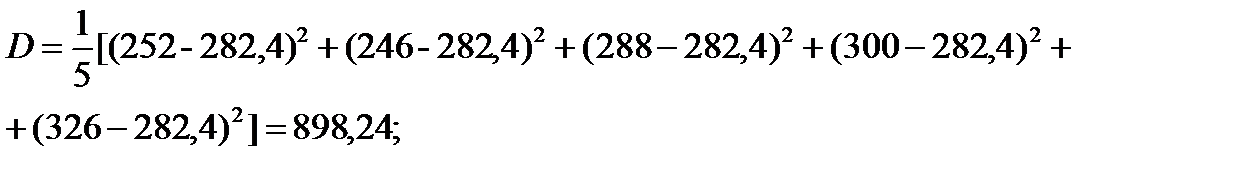
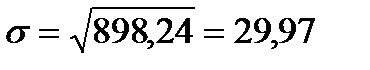 ;
;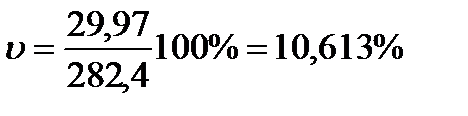 .
.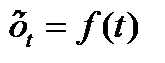 (8)
(8)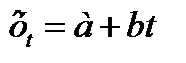 , (9)
, (9)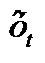 - расчётное значение числа пожаров в t – м году; а и b – коэффициенты; t - номер года.
- расчётное значение числа пожаров в t – м году; а и b – коэффициенты; t - номер года. , была минимальной, т.е. отвечала условию:
, была минимальной, т.е. отвечала условию: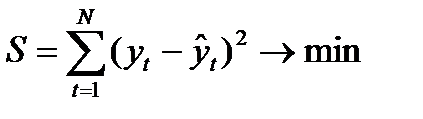 . (10)
. (10)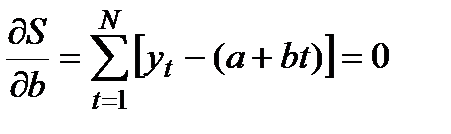 ; (11)
; (11)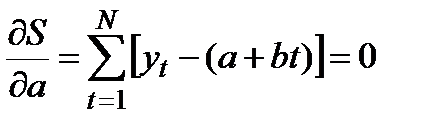 , (12)
, (12)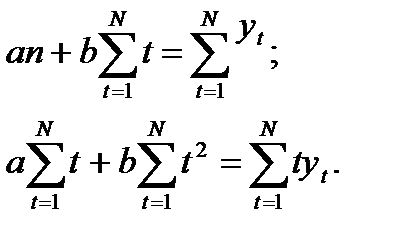 (13)
(13)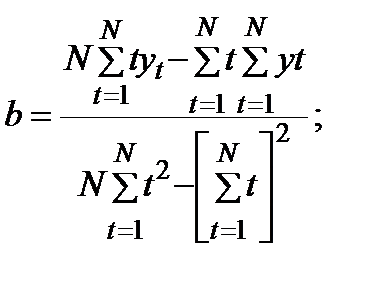 (14)
(14) (15)
(15)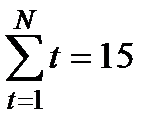
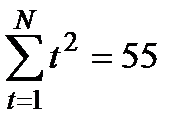
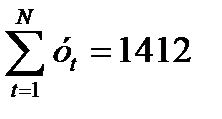
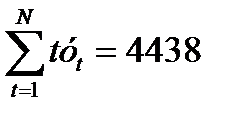
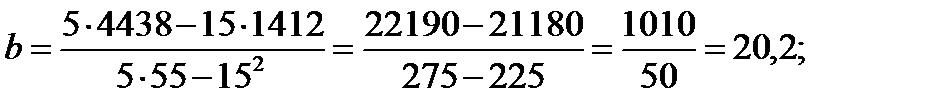

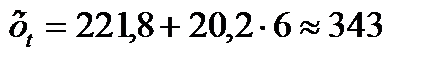 .
.




