
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операции над классами (множествами)Содержание книги
Поиск на нашем сайте
Класс, или множество (то есть совокупность предметов, охватываемая объемом понятия) может включать в себя подклассы, или подмножества. Так, например, класс «городов» включает в себя подкласс «городов России», класс «рек» – подкласс «рек Сибири» и т.д. Понятие, из объема которого происходит выделение подкласса, называется родовым или родом; понятие, объем которого выделяется из родового понятия – видовым или видом (например, наука – родовое понятие, химия – видовое). При рассмотрении операций над классами в логике вводятся следующие обозначения: А, В, С …– произвольные классы; 1 – универсальный класс; 0 – пустой класс; È – знак объединения классов (сложения); Ç – знак пересечения классов (умножения); А´, ( Операции над классами иллюстрируются круговыми схемами, универсальный класс обозначается прямоугольником. Класс (множество) – это совокупность предметов, которые можно мыслить вместе на основании удовлетворения ими каким-либо условиям или признакам. Классы могут быть единичными, то есть состоящими только из одного элемента; конечными, состоящими из конечного числа элементов; бесконечными – элементы которых принципиально не допускают пересчета, например, бесконечным классом является класс всех четных чисел; неопределенными; пустыми, то есть вовсе не содержать элементов и универсальными, которые противополагаются пустым классам и состоят из всех объектов подлежащей рассмотрению предметной области. Подкласс (подмножество) – это такое множество, каждый элемент которого в то же время является элементом более широкого множества. Из двух и более классов с помощью определенных операций можно образовать новый класс. Основными операциями над классами являются объединение классов (сложение), пересечение классов (умножение), образование дополнения к классу (отрицание) и вычитание класса (разность). Объединением классов (сложением) называется логическая операция, в результате которой образуется новый класс, состоящий из таких объектов, каждый из которых является элементом, по крайней мере, одного из слагаемых классов. Полученный в результате сложения класс АÈВ называется суммой.
А – класс депутатов Государственной Думы. В – класс юристов. АÈВ – класс, содержащий всех депутатов Госдумы и всех юристов. · Свойства объединения (сложения): AÈB=BÈA AÈB=ù(ùAÇùB) AÈ0=A AÈ(BÈC)=(AÈB) ÈC AÈ(BÇC)=(AÈB)Ç(AÈC) ùAÈùB=ù(AÇB) AÈA=A AÈ1=1 · Операция объединения (сложения) над классами, объемы которых находятся в разных отношениях: Равнозначность: AÈB=A, AÈB=B
= = Пересечение (частичное совпадение): AÈB=AB
Подчинение: AÈB=A
= Соподчинение: AÈB=С
= Противоположность: AÈB=A, AÈB=В, AÈB¹AВ
= или, но не А и В (АВ). Противоречие: AÈB=С
=
Например: Произведением классов «студент» (А) и «шахматист» (В) является новый класс «студент-шахматист» (АÇВ). При умножении множеств, находящихся в отношении несовместимости, получается нулевой класс. Например, умножение классов «гуси» и «утки» дает пустое множество, так как нет таких объектов, которые одновременно были бы и гусями и утками. · Свойства пересечения (умножения): AÇB=BÇA AÇA=A ùAÈùB=ù (AÇB) AÇ(BÇC)=(AÇB)ÇC AÇ1=A AÇ0=A AÇB=ù (ùAÈùB) · Операция пересечения (умножения) над классами, объемы которых находятся в разных отношениях: Равнозначность: AÇB=A, AÇB=B
= = Пересечение (частичное совпадение): AÇB=С
= А и В Подчинение: AÇB=B
= Соподчинение: AÇB=Æ
= Æ Противоположность: AÇB=Æ
= Æ Противоречие: AÇB=Æ
= Æ Вычитанием классов (разностью) – называется логическая операция, в результате которой образуется новый класс, состоящий из элементов уменьшаемого класса, не принадлежащих вычитаемому классу.
А – класс «химический элемент». В – класс «металл». В результате вычитания получается класс, состоящий из химических элементов, не являющихся металлами. · Свойства вычитания (разности): A/А=Æ A/ùA =А ùA/А=ùA · Операция вычитания (разности) над классами, объемы которых находятся в разных отношениях: Равнозначность: A/B=В/A=Æ
= Æ Пересечение (частичное совпадение): A/B=А и ùВ, В/А=В и ùA
= А/В = А и ùВ
= А/В = В и ùA
Подчинение: A/B= А и ùB, В/А=Æ
= A/B = А и ùB Соподчинение: A/B=А, В/А=В
= A/B = А
= В/А = В Противоположность: A/B=А, В/А=В
= A/B = А
= В/А = В
Противоречие: A/B=А, В/А=В
= A/B = А
= В/А = В Образованием дополнения к классу (отрицанием) – называется логическая операция, состоящая в образовании нового класса А´ (
Между объединением, пересечением и отрицанием работают следующие равносильности:
· Свойства дополнения: Отношения между дополняемым классом и его дополнением есть отношения противоречия, которое характеризуется тем, что каждый из объектов какой-нибудь универсальной области может мыслиться в объеме только одного из противоречащих понятий. Из этого свойства противоречащих понятий вытекают все законы операции дополнения. 1. Сумма класса и его дополнения равна универсальному классу:
АÈA'=1. 2. Сумма дополняемого класса и универсума равна универсальному классу: АÈ1=1. 3.
Произведение дополняемого класса и универсума равно дополняемому классу: АÇ1=А. 4. Произведение класса и его дополнение является пустым классом: АÇA'=0. 5. Сумма пустого класса с произвольным классом равна этому классу: AÈ0=A. 6. Произведение пустого класса с произвольным классом является пустым классом: АÇ0=0. 7. Дополнением универсума является пустой класс: 1'=0. 8. Дополнением пустого класса является универсум: 0'=1. 9. Дополнением дополнения является дополняемый класс: (A')'=A. Делением классов (обратным умножением) – называется логическая операция, в результате которой образуется новый класс, состоящий из определенной части делимых классов. · Операция деления (обратного умножения) над классами, объемы которых находятся в разных отношениях: Равнозначность: (AÇВ):А=(АÇB):В=A=В
= = = А = В Пересечение (частичное совпадение): (AÇВ):А=В, (АÇB):В=A
= (AÇВ):А = В
= (AÇВ):В = A
Подчинение: (AÇВ):А=В, (АÇB):В=A
= = (AÇВ):В = А
|
||||||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 596; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.007 с.) |

 ; ù А) – дополнение к классу А.
; ù А) – дополнение к классу А. Например:
Например:
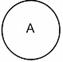

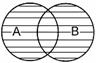
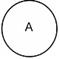




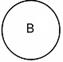


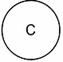
 Пересечением классов (умножением) – называется логическая операция, в результате которой образуется новый класс, состоящий из общих умножаемым классам элементов. Класс АÇВ, полученный в результате умножения, называется произведением.
Пересечением классов (умножением) – называется логическая операция, в результате которой образуется новый класс, состоящий из общих умножаемым классам элементов. Класс АÇВ, полученный в результате умножения, называется произведением.




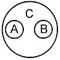


 Например: А/В
Например: А/В








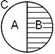
 Чтобы образовать дополнение, нужно класс А исключить из универсального класса: 1-А=А´. Например, чтобы образовать дополнение к классу «студент», надо подвергнуть этот класс отрицанию. Полученный класс «не-студент» является дополнением к классу «студент». Класс студентов, сложенный с классом «не-студентов», образует универсальный класс учащихся (AÈA´=1).
Чтобы образовать дополнение, нужно класс А исключить из универсального класса: 1-А=А´. Например, чтобы образовать дополнение к классу «студент», надо подвергнуть этот класс отрицанию. Полученный класс «не-студент» является дополнением к классу «студент». Класс студентов, сложенный с классом «не-студентов», образует универсальный класс учащихся (AÈA´=1). ;
; 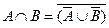 ;
;  ;
; 











