
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Б2. 1. Банахово пространствоСтр 1 из 4Следующая ⇒
Б2. 1. Банахово пространство
2.3.4.5.6.
Б2. 7. Сингулярные функции
Сингулярная функция — это непрерывная функция, производная которой равна нулю почти всюду. Исторически первым примером сингулярной функции является Канторова лестница. Существуют другие примеры сингулярных функций. Например, и функция Минковского, множество точек роста которых заполняет полностью отрезок Сингулярная функция встречается, к примеру, при изучении последовательности пространственно модифицированных фаз или структур в твёрдых телах и магнетиках, описываемых в модели Френкеля — Конторовой. Сингулярной обобщенной функции являтся
Отличная от постоянной непрерывная функция с конечным изменением, производная которой почти везде равна нулю, называется сингулярной функцией.
Б2. 8. Обобщенные производные
Лемма 1. Если Лемма 2. Обобщённая производная определяется с точностью до эквивалентности. Обобщённые производные сохраняют некоторые свойства обычных производных: 1) Если 2) Если 3) Из определения обобщённой производной следует, что она независит от порядка дифференцирования. 3) Другим важным отличием обобщённых производных от классических является то, что обобщённые производные определяются с точностью до множества меры ноль. Б2. 9. Счетные множества
Одним из немаловажных понятий теории множеств является понятие счетного множества. Но прежде чем ввести это понятие, необходимо усвоить и разъяснить некоторые элементарные понятия и определения. Определение 1. Множество называется конечным, если количество элементов этого множества есть конечное число. Если же количество элементов множества есть число бесконечное, то множество называется бесконечным.
Б2. 12. Пространства Лебега
Рассмотрим один важнейший вид банаховых пространств. Зафиксируем действительное число
Полученные таким образом пространства (ниже мы убедимся, что эти пространства банаховы при любом Вообще говоря, в современной математике используются несколько различных понятий определенного интеграла. Наиболее употребимыми из них являются интеграл Римана (именно его обычно изучают в классическом курсе анализа) и интеграл Лебега. Как явствует из самого названия, при рассмотрении классов Лебега Понятие интеграла Лебега - более общее, чем интеграла Римана. Функция, интегрируемая на [a, b] по Риману, интегрируема и по Лебегу (причем значения интегралов совпадают), но обратное, вообще говоря, неверно.
Б2. 15 Неравенство Чебышева
Формулировка Если
Доказательство Для
Следствие Как следствие получим так называемое "правило трех сигм",которое означает, что вероятность случайной величины отличаться от своего математического ожидания более чем на три корня из дисперсии мала. Рассмотрим такое утверждение: Если
Доказательство: Согласно неравенству Чебышева
Отсюда заметим, что вероятность отклониться значению случайной величины от значения математического ожидания меньше чем
Доказательство. Так как система векторов Добавим к исходной системе векторов еще s векторов
2. Если из линейно независимой системы векторов Доказательство. Предположим, что полученная система линейно зависима. Добавив к этой системе векторов все отброшенные векторы, мы получим исходную систему векторов. По условию – она линейно независима, а в силу предыдущего свойства линейной зависимости она должна быть линейно зависимой. Мы пришли к противоречию, следовательно, наше предположение неверно. 3. Если в системе векторов Доказательство. Пусть вектор 4. Если система векторов 5. Доказательство. Сначала докажем первое утверждение. Пусть система векторов Теперь докажем второе утверждение. Так как система векторов Предположим, что какой-нибудь вектор системы Из двух последних свойств следует важное утверждение:
Б2. 20. Примеры ортонормированных базисов · Стандартный базис
· Множество
· Примером ортонормированного базиса является стандартный базис пространства Rn (если скалярное произведение в Rn определить как сумму произведений одноименных компонент). · Векторы i, j образуют ортонормированный базис в пространстве · В гильбертовом пространстве L2 [-p;p] функций суммируемых с квадратом модуля на отрезке [-p;p] функции 1, cos t, sin t, sin 2t,… образуют ортогональный базис. Однако эта система функций не является нормированной.
·
Б2. 21. Неравенство Бесселя
Б2. 1. Банахово пространство
2.3.4.5.6.
Б2. 7. Сингулярные функции
Сингулярная функция — это непрерывная функция, производная которой равна нулю почти всюду. Исторически первым примером сингулярной функции является Канторова лестница. Существуют другие примеры сингулярных функций. Например, и функция Минковского, множество точек роста которых заполняет полностью отрезок Сингулярная функция встречается, к примеру, при изучении последовательности пространственно модифицированных фаз или структур в твёрдых телах и магнетиках, описываемых в модели Френкеля — Конторовой. Сингулярной обобщенной функции являтся
Отличная от постоянной непрерывная функция с конечным изменением, производная которой почти везде равна нулю, называется сингулярной функцией.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 545; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.227.76 (0.029 с.) |




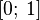 .
.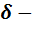 функция Дирака
функция Дирака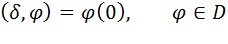
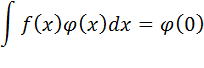

 есть обычная производная, определённая в каждой точке
есть обычная производная, определённая в каждой точке  , тогда
, тогда  является обобщённой производной от
является обобщённой производной от  порядка
порядка  .
. и
и 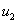 имеют обобщённую производную в
имеют обобщённую производную в  также имеет обобщённую производную в
также имеет обобщённую производную в 
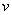 есть обобщённая производная вида
есть обобщённая производная вида  , а
, а  есть обобщённая производная вида
есть обобщённая производная вида  , то
, то 





 и некоторый отрезок [a, b]. Рассмотрим на [a, b] множество всех комплекно значных функций f(x), для которых существует
и некоторый отрезок [a, b]. Рассмотрим на [a, b] множество всех комплекно значных функций f(x), для которых существует  . Операции сложения функций и умножения функции на комплексное число определим обычным образом. Норму определим как
. Операции сложения функций и умножения функции на комплексное число определим обычным образом. Норму определим как

 используется интеграл Лебега.
используется интеграл Лебега. , то
, то  будет выполнено
будет выполнено
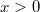 неравенство
неравенство  равносильно неравенству
равносильно неравенству  , поэтому
, поэтому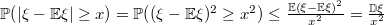
 .
.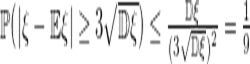

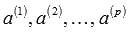 линейно зависима, то равенство
линейно зависима, то равенство  возможно при наличии хотя бы одного ненулевого числа из чисел
возможно при наличии хотя бы одного ненулевого числа из чисел  . Пусть
. Пусть 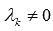 .
.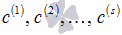 , при этом получим систему
, при этом получим систему  . Так как
. Так как  , то линейная комбинация векторов этой системы вида
, то линейная комбинация векторов этой системы вида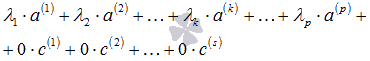
 в этой системе векторов является нулевым. Предположим, что исходная система векторов линейно независима. Тогда векторное равенство
в этой системе векторов является нулевым. Предположим, что исходная система векторов линейно независима. Тогда векторное равенство  . Однако, если взять любое
. Однако, если взять любое  , отличное от нуля, то равенство
, отличное от нуля, то равенство 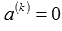 . Следовательно, наше предположение неверно, и исходная система векторов линейно зависима.
. Следовательно, наше предположение неверно, и исходная система векторов линейно зависима.
 возможно лишь при
возможно лишь при 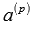 , тогда
, тогда 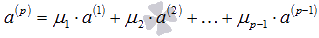 . Это равенство можно переписать как
. Это равенство можно переписать как  , в его левой части находится линейная комбинация векторов системы, причем коэффициент перед вектором
, в его левой части находится линейная комбинация векторов системы, причем коэффициент перед вектором  и
и  , где
, где  – произвольное число, то она линейно зависима.
– произвольное число, то она линейно зависима. в n-мерном евклидовом пространстве R n является ортонормированным.
в n-мерном евклидовом пространстве R n является ортонормированным. образует ортонормированный базис в L2([-π, π]).
образует ортонормированный базис в L2([-π, π]). свободных векторов на плоскости. Точно так же векторы i, j, k образуют ортонормированный базис в пространстве.
свободных векторов на плоскости. Точно так же векторы i, j, k образуют ортонормированный базис в пространстве.







