
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Б2. 8. Обобщенные производные
Лемма 1. Если Лемма 2. Обобщённая производная определяется с точностью до эквивалентности. Обобщённые производные сохраняют некоторые свойства обычных производных: 1) Если 2) Если 3) Из определения обобщённой производной следует, что она независит от порядка дифференцирования. 3) Другим важным отличием обобщённых производных от классических является то, что обобщённые производные определяются с точностью до множества меры ноль. Б2. 9. Счетные множества
Одним из немаловажных понятий теории множеств является понятие счетного множества. Но прежде чем ввести это понятие, необходимо усвоить и разъяснить некоторые элементарные понятия и определения. Определение 1. Множество называется конечным, если количество элементов этого множества есть конечное число. Если же количество элементов множества есть число бесконечное, то множество называется бесконечным.
Б2. 10. Множества мощности континиуум Мощность множества, кардинальное число множества (лат. cardinalis ← cardo — главное обстоятельство, стержень, сердцевина) — характеристика множеств (в том числе бесконечных), обобщающая понятие количества (числа) элементов конечного множества.
В основе этого понятия лежат естественные представления о сравнении множеств: 1. Любые два множества, между элементами которых может быть установлено взаимно-однозначное соответствие (биекция), содержат одинаковое количество элементов (имеют одинаковую мощность). 2. Обратно: множества, равные по мощности, должны допускать такое взаимно-однозначное соответствие. 3. Часть множества не превосходит полного множества по мощности (то есть по количеству элементов) Теорема. Множество, эквивалентное множеству всех точек отрезка [0, 1] называется множеством мощности континуума. Так как множества точек интервалов, отрезков и всей прямой эквивалентны между собой, то все они имеют мощность континуума.
Следствие. Множество вещественных чисел имеет мощность континуума. Вспомним, что счетное множество – самое “маленькое” из всех бесконечных множеств. Поэтому можно сказать, что вещественных чисел гораздо больше, чем рациональных – ведь вещественных чисел континуум, а рациональных – всего лишь счетное множество.
|
|||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 351; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.249.158 (0.003 с.) |

 есть обычная производная, определённая в каждой точке
есть обычная производная, определённая в каждой точке  , тогда
, тогда  является обобщённой производной от
является обобщённой производной от  порядка
порядка  .
. и
и 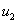 имеют обобщённую производную в
имеют обобщённую производную в  также имеет обобщённую производную в
также имеет обобщённую производную в 
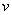 есть обобщённая производная вида
есть обобщённая производная вида  , а
, а  есть обобщённая производная вида
есть обобщённая производная вида  , то
, то 










