Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
С использованием типовых функцийСодержание книги
Поиск на нашем сайте
В соответствии с данным методом вид функции задается аксиоматически, а ее параметры непосредственно оцениваются лицом, принимающим решения. Например, в случае треугольной формы функции принадлежности ЛПР указывает такие ее параметры u1, u2, u3при которых она принимает единичное и нулевые значения, т. е. Параметрическое представление функций принадлежности является компактным, обеспечивает простоту построения их на практике, однако связано с исследованием адекватности используемых форм (треугольной, трапециевидной, колоколообразной и др.) и соответствующих аналитических описаний функции принадлежности . Конкретный вид функций принадлежности определяется на основе различных дополнительных предположений о свойствах этих функций (симметричность, монотонность, непрерывность первой производной и т.д.) с учетом специфики имеющейся неопределенности.
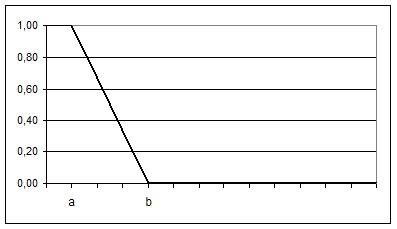
Для построения значений ФП используются функции: 1)
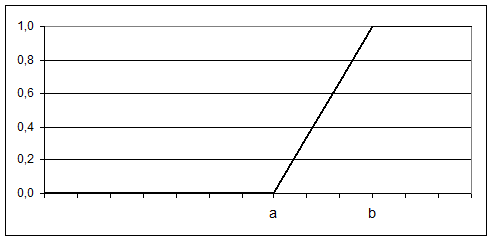
Рисунок 22 – ФП для выражения (1) 2)
Рисунок 23 – ФП для выражения (3)
3)
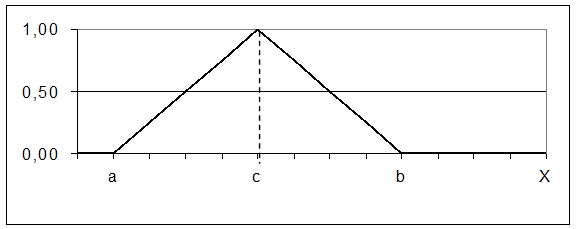
Рисунок 24 – ФП для выражения (3) 4)
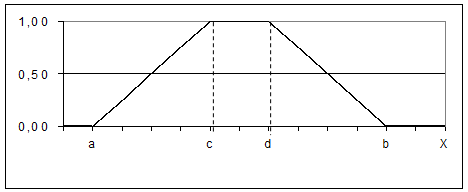
Рисунок 25 – ФП для выражения (4) 5)
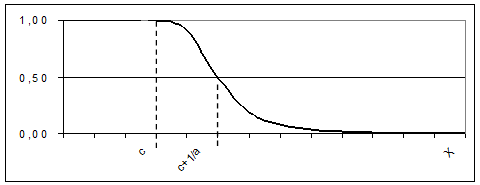
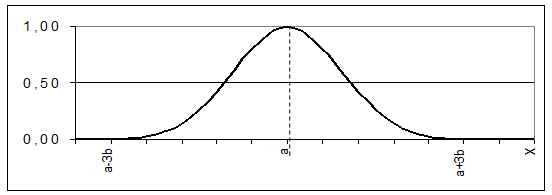
Рисунок 26 – ФП для выражения (5) 6) Рисунок 27 – ФП для выражения (6)
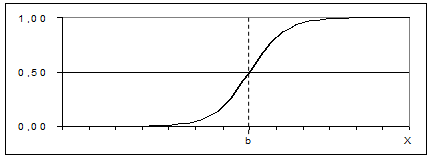
7)
Рисунок 28 – ФП для выражения (7) Операции над нечеткими множествами Подобно операциям над четкими множествами, нечеткие множества также можно пересекать, объединять и инвертировать. Л. Заде предложил оператор минимума для пересечения и оператор максимума для объединения двух нечетких множеств. Видно, что эти операторы совпадают с объединением и пересечением, если мы рассматриваем только степени принадлежности 0 и 1. ОПЕРАЦИЯ ОБЪЕДИНЕНИЯ Объединением нечетких множеств
где
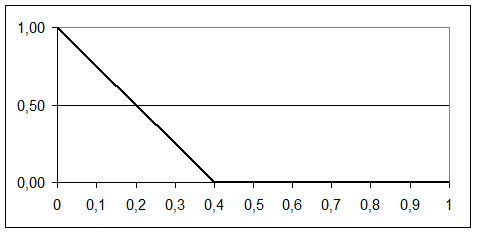
Предположим, на интервале от [0; 0,4] функция принадлежности (ФП) описывается выражением (1):
Графическое изображение функции (1) при a=0 и b=0,4 приведено на рисунке 29.
Рисунок 29 – ФП для выражения (1)
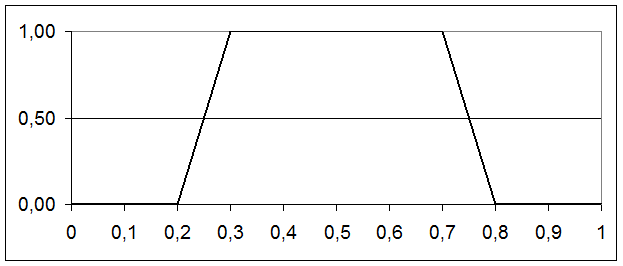
Предположим, на интервале [0,2; 0,8] функция принадлежности описывается выражением (2):
Графическое изображение функции (1) при a=0,2; c=0,3; d=0,7; b=0,8 приведено на рисунке 30.
Рисунок 30 – ФП для выражения (2)
Тогда в результате выполнения операции объединения общий вид ФП будет такой (рисунок 31).
Рисунок 31 – Результат выполнения операции объединения
ОПЕРАЦИЯ ПЕРЕСЕЧЕНИЯ
Пересечением нечетких множеств Ã и B̃ называется множество:
Где
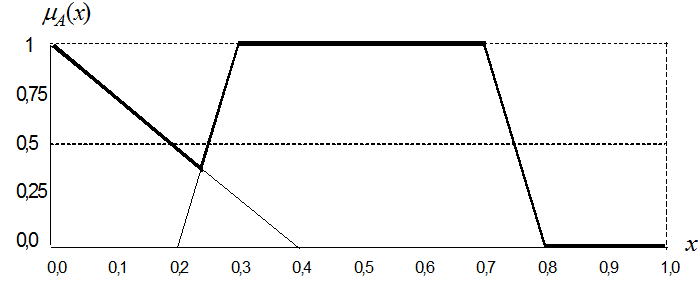
Для условий предыдущего примера результат операции пересечения будет иметь вид (рисунок 32):
Рисунок 32 – Результат выполнения операции пересечения
ОПЕРАЦИЯ ДОПОЛНЕНИЯ
Дополнением нечеткого множества Ã называется множество
где
Носителем нечёткого множества Предположим, на интервале от [0,1; 0,5] функция принадлежности описывается выражением (3):
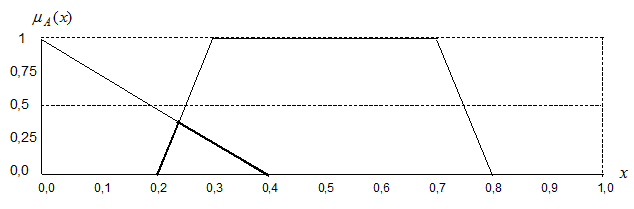
Графическое изображение функции (3) при a=0,1 c=0,3 и b=0,5 приведено на рисунке 33. На этом же рисунке приведена и функция
Рисунок 33 – Результат выполнения операции дополнения
|
||||||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 257; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.32.115 (0.005 с.) |

 и для всех
и для всех 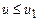 ,
,  имеет место
имеет место 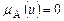 .
.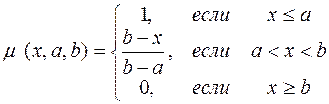 (1)
(1)
 (2)
(2)
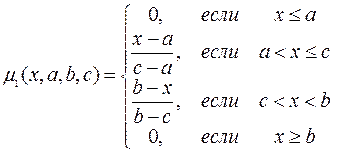 (3)
(3)
 (4)
(4)
 (5)
(5)
 (6)
(6)
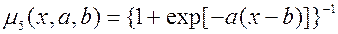 (7)
(7)
 и
и 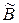 называется множество:
называется множество: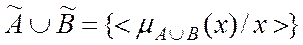 ,
,
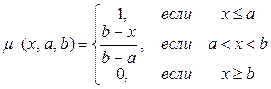 (1)
(1)
 (2)
(2)
 ,
,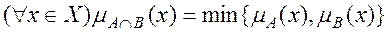 .
.
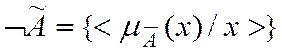 ,
,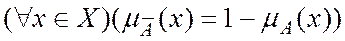 .
.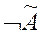 ̃ будет являться множество
̃ будет являться множество  , т. е. множество тех элементов
, т. е. множество тех элементов 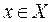 , для которых функция принадлежности
, для которых функция принадлежности 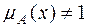 .
. (3)
(3)