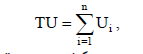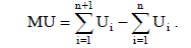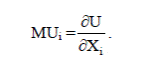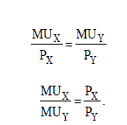Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Корисність і уподобання в економічній теорії. Закон спадної граничної корисності.Содержание книги
Поиск на нашем сайте
Корисність - це здатність даного товару чи послуги задовольнити потребу споживача, бажання та уподобання. Корисність товару – це здатність товару задовольняти споживача і приносити йому певну корисність. Не можна корисність порівнювати з користю. Наведемо невеликий приклад: (наприклад користуванням автомобілем приносить нам корисність, а наприклад куріння навпаки - шкоду). Властивості корисності товару: 1. Корисність товару є різною для різних людей, оскільки залежить від індивідуальних смаків, уподобань і потреб споживача. 2. Корисність від певних благ є різною для однієї і тієї ж людини у різний час і за різних обставин (до цієї властивості є дуже цікавий приклад: Наприклад візьмемо морозиво. Звичайно, що влітку попит на морозиво і корисність від нього буде більшою, адже взимку споживання морозива є дуже мала і потреба споживача не буде високою). Сума корисності декількох товарів показує, яку корисність принесли нам ці товари. Функція корисності — це співвідношення між обсягами споживаних благ і рівнем корисності, який досягається при цьому споживачем: U = f (X1; X2;..., Xn), де U — рівень корисності (від англ. utility); X1; X2;..., Xn — кількості споживаних благ. Загальна корисність — це сума корисностей всіх наявних у споживача одиниць цього блага:
Сукупна корисність (TU) – це сума задоволення від споживання благ. Вона може бути представлена у вигляді функції, яка показує залежність корисності від загальної кількості споживаних благ: TU = f (X,Y) де X,Y – кількості споживаних благ. Для оцінки зміни сукупної корисності вводиться поняття граничної корисності. Можна дати кілька визначень граничної корисності. Гранична корисність (MU) – це зміна сукупної корисності набору товарів при зміні кількості даного блага на одиницю. Це – приріст сукупної корисності. Іншими словами: гранична корисність – це додаткова корисність, одержана від споживання додаткової одиниці блага. Математично граничні корисності благ можна представити як часткові похідні функції сукупної корисності:
Спостереження за поведінкою споживача дозволило Г. Госсену зробити висновок, що блага мають цінність для індивіда тільки у випадку, коли їх кількість менша за необхідну, причому цінність кожної наступної одиниці блага зменшується. Його теорія споживання включає два закони. Перший закон Госсена одержав назву закону спадної граничної корисності. Він сформульований так: величина задоволення від споживання кожної додаткової одиниці благ даного виду зменшується, доки не досягне нуля у точці повного насичення потреби. Дія цього закону описується функцією корисності з одним змінним благом. Другий закон Госсена стосується споживання кількох благ, вибору споживача. Розглянемо спрощену модель максимізації корисності для випадку споживання одного блага X. Функція сукупної корисності тепер має вигляд: TU = f (X).
Проілюструємо перший закон Госсена за допомогою умовних даних (табл.. 4.1). Припустимо, що споживач нарощує споживання блага X від 0 до 8 одиниць (колонка 1). Динаміка сукупного задоволення () X TU показана в колонці 2. Зміни сукупної корисності, тобто граничну корисність (колонка 3) одержуємо за формулою
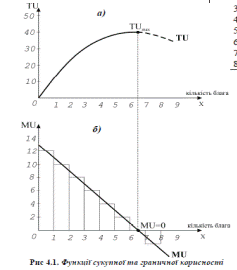
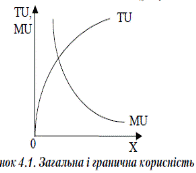
Таким чином, між кривими сукупної та граничної корисності існує геометричний зв’язок: - крива сукупної корисності досягає максимального значення в точці, дегранична корисність рівна нулю;
- величину граничної корисності показує кут нахилу кривої сукупної корисності - за від’ємних значень граничної корисності крива TU відхиляється донизу, але цей відрізок (його показано пунктиром) не включається у функцію корисності. 2. Рівновага споживача за кардиналістським підходом. Кількісна (кардиналістська) функція корисності має місце в тому випадку, коли ми не тільки можемо визначити розташування і послідовність класів байдужості, а і вказуємо, як ми оцінюємо різницю в рівнях добробуту, що відповідають кожному з таких класів. Гіпотези кількісної теорії корисності: 1. Споживач витрачає свій бюджет таким чином, щоб одержати максимальне задоволення від сукупного споживання благ. 2. Споживач може висловити своє бажання придбати деяку кількість блага за допомогою кількісної оцінки корисності цього блага. Одиниця, яка є масштабом виміру корисності — ютіль. При цьому кожний вид блага має для споживача загальну корисність і граничну. Загальна корисність — це сума корисностей всіх наявних у споживача одиниць цього блага:
де Ui — корисність ітої одиниці блага в ютілях; n — кількість одиниць блага. Гранична корисність — це зміна загальної корисності набору благ при зміні кількості даного блага на одиницю.
При диференційованості функції споживання гранична корисність блага даного іго виду є першою частковою похідною функції корисності U, яка виражає загальний рівень добробуту даного споживача в даній ситуації (по змінній Xi, що відповідає величині споживаного блага даного іго виду) і позначається MU(Xi) або MUi:
Другий закон Госсена: споживач при заданих цінах та бюджеті максимізує свою функцію корисності, якщо виконується наступна умова рівноваги:
Згідно з цією умовою, споживач, який максимізує корисність, купує товари в таких обсягах, щоб їхні граничні корисності у розрахунку на одну грошову одиницю були рівними. 3.Криві байдужості, їх властивості. Карта кривих байдужості. Крива байдужості — це крива, кожна точка якої характеризує споживацький вибір у вигляді певного набору товарів чи послуг (ринковий кошик або кошик споживача) (рис. 3.2).
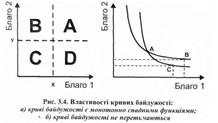
Ринковий кошик (споживчий кошик) — це комбінація товарів X і У для споживання їх протягом певного часу. Споживач не розрізняє набори товарів X і У, які розташовані на кривій байдужості и. Рівень корисності кожного з наборів на кривій байдужості однаковий. Тому можна вважати, що крива байдужості показує альтернативні набори товарів, які забезпечують однаковий рівень корисності. Карта кривих байдужості — це засіб відображення переваг споживача, що відповідають різному рівню задоволення його потреб (рис. 3.3). Карта кривих байдужості складається з безлічі ліній, що не перетинаються. Властивості кривих байдужості1: 1. Криві байдужості с монотонно спадними функціями (при збільшенні кількості певного блага значення функції спадає). Зафіксуємо деякий набір (X, У) пари благ 1 та 2 і розглянемо, в яких частинах площини можуть перебувати еквівалентні набори. Іншими словами, нас цікавлять набори, які перебувають на тій самій поверхні байдужості, що і (X, У) (рис. 3.4, а).
Очевидно, що поверхня байдужості, яка містить набір (X, У), не буде проходити в областях А та С, оскільки ці області містять відповідно заздалегідь кращі та гірші набори благ 1 та 2. Методом вилучення ми дійшли висновку, що можливими областями, через які проходитиме поверхня байдужості, яка містить набір (X, У), можуть бути лише області В та Э, тобто вона є монотонно спадною функцією.
2. Поверхні байдужості не перетинаються. Припустимо протилежне: нехай поверхні байдужості перетинаються і мають спільну точку А (рис. 3.4, б). Отже, вони відображають дві множини наборів благ, еквівалентних з погляду споживача, тобто 11а= 1Ы ид= ІІс, отже, ІІв= ІІс. У той же час точка С менш приваблива порівняно з точкою В, оскільки набір В містить більше і блага 1, і блага 2. Помічена суперечність дає підставу для твердження про неприпустимість перетину поверхонь байдужості. 3. При збільшенні споживання певного блага зменшується величина іншого, яку людина жертвує заради отримання додаткової одиниці першого блага (прояв закону спадної граничної корисності). Якщо у людини, наприклад, багато одягу, але мало їжі, то заради додаткової одиниці їжі вона схильна пожертвувати значною часткою одягу. Якщо ж людина має багато їжі, то заради додаткової одиниці їжі вона вже буде схильна жертвувати вже меншою часткою гардеробу.Мовою графіки та математики це означає, що кут нахилу поверхні байдужості до горизонтальної осі зменшується при збільшенні споживання блага, величина якого відображається на цій осі. Іншими словами, поверхні байдужості є опуклими функціями (рис. 3.5) 4* Чим більше поверхня байдужості віддалена від почат-
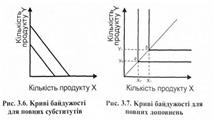
ку координат, тим привабливішими для людини є набори благ, які розташовані на цій поверхні. Ця властивість навіть не потребує доведення: вона випливає з самих умов надання переваг (див. параграф 3.1). Чим більше в наборі благ, тим він корисніший. ■ Криві байдужості особливого типу. Існують групи товарів і послуг, що мають криві байдужості особливого типу': /. Повні субститути (замінники) — товари, які повністю можуть бути замінені один одним з постійним коефіцієнтом заміни (рис. 3.6).
Карти кривих байдужості для повних субститутів складаються із серій паралельних прямих, оскільки МЯБух постійна по мірі пересування вздовж кривої байдужості. Повні субститути, для яких МІ18ух= 1, одержали назву го-могенів. Наприклад, якщо покупець вважає, що пляшка кефіру, куплена в будь-якому магазині міста, ідентична, то це гомогенний товар. Якщо два літри молока, купленого в магазині, за своїми якостями рівноцінні літру молока, купленого на базарі, то маємо повний субститут з МК.8ху= 2. 2. Повні доповнення — товари, які можуть споживатися в фіксованій пропорції.
Карти кривих байдужості для повних доповнень (рис. 3.7) показують, що для споживання товару X у певній кількості потрібна певна кількість товару У. їх співвідношення визначене точками, розташованими на прямій, яка виходить із початку координат під кутом, визначеним 'мінімальним необхідним співвідношенням: - для набору а це (х0, у0); - для набору Ь — (х„ у,), хоч будь-який із товарів можна придбати додатково у будь-якій кількості. Шкідливі товари — це та група товарів, споживання яких шкідливе для споживача. Прикладом є інтенсивність функціонування підприємств і забруднення навколишнього середовища. Криві байдужості для таких товарів (рис. 3.8, а) показують, що з інтенсифікацією виробництва зростає забруднення навколишнього середовища.
Тепер побудуємо криву байдужості, яка відображає взаємозв'язок між забрудненням навколишнього середовища і компенсацією цієї обставини у вигляді збільшення кількості робочих місць. Тут спостерігається парадоксальне явище: виявляється, людина звикає до шкідливих впливів, вимагаючи все менше компенсацій (рис. 3.8, б), тобто крива байдужості є опуклою догори функцією. Гранична норма заміщення благ. Аналізуючи криві байдужості, необхідно звернути увагу на здатність товарів до взаємо-замінювання. Якщо для спрощення ситуації розглянути набір споживача, що складається лише з двох благ, наприклад, молока і Хліба, то зменшення споживання молока на певну кількість може бути компенсоване збільшенням споживання хліба і навпаки. При цьому споживач буде на одній і тій самій кривій байдужості, тобто отримуватиме однакове задоволення. Гранична норма заміщення (субституції) — це кількість товару У, від якої споживач відмовився б, щоб отримати ще одну одиницю товару X, залишаючись на цій же кривій байдужості. Як бачимо на рис. 3.9, зменшення обсягу споживання товару X на АХ (Х-,- X,) компенсується збільшенням споживання товару У на ДУ (У2-У|). Тому граничну норму заміщення (МЯБху) можна розрахувати так: МЯБху = (ЛУ/ЛХ) (3.1) Гранична норма заміщення завжди виражається від'ємним числом (МЯБху < 0), адже АХ < 0, оскільки Х,< X.. На це потрібно звернути особливу увагу, тому що деякі автори, щоб показати, що МЯБху < 0, помилково ставлять перед дробом знак Насправді ж цей "мінус" не потрібний, оскільки він "захований" у самому АХ.
|
||||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 323; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.54.190 (0.009 с.) |

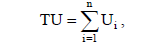
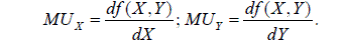
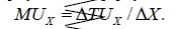 Графік 4.1.а) показує, що сукупна корисність представляє собою зростаючу опуклу вгору функцію. Тенденцію зростання розглядають як закон зростаючої сукупної корисності, який формулюється таким чином: з нарощуванням споживання будь-якого блага загальна сума корисності зростає. Опуклість функції вгору означає, що прирости сукупної корисності додатні, але зменшуються. Якщо зобразити ці прирости окремим графіком, то одержимо функцію граничної корисності. Спрощено графік граничної корисності можна показати у вигляді гістограми (рис. 4.1. б). Якщо припустити, що благо може ділитись на нескінченно малі частини, то, з’єднавши середини інтервалів кожного зі стовпчиків гістограми, ми одержимо безперервну функцію граничної корисності, яка має вигляд спадної кривої. Теоретично можна уявити від’ємне значення граничної корисності. Але оскільки ми виходимо з фундаментального припущення про рідкісність благ, то раціональна поведінка споживача передбачає споживання блага лише до точки, де гранична корисність стає рівною нулю. В цій точці сукупна корисність максимізується.
Графік 4.1.а) показує, що сукупна корисність представляє собою зростаючу опуклу вгору функцію. Тенденцію зростання розглядають як закон зростаючої сукупної корисності, який формулюється таким чином: з нарощуванням споживання будь-якого блага загальна сума корисності зростає. Опуклість функції вгору означає, що прирости сукупної корисності додатні, але зменшуються. Якщо зобразити ці прирости окремим графіком, то одержимо функцію граничної корисності. Спрощено графік граничної корисності можна показати у вигляді гістограми (рис. 4.1. б). Якщо припустити, що благо може ділитись на нескінченно малі частини, то, з’єднавши середини інтервалів кожного зі стовпчиків гістограми, ми одержимо безперервну функцію граничної корисності, яка має вигляд спадної кривої. Теоретично можна уявити від’ємне значення граничної корисності. Але оскільки ми виходимо з фундаментального припущення про рідкісність благ, то раціональна поведінка споживача передбачає споживання блага лише до точки, де гранична корисність стає рівною нулю. В цій точці сукупна корисність максимізується.