
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Для схемы замещения, приведенной на рисунке 1. 5, Направленный граф электрической сети имеет следующий вид.Содержание книги
Поиск на нашем сайте
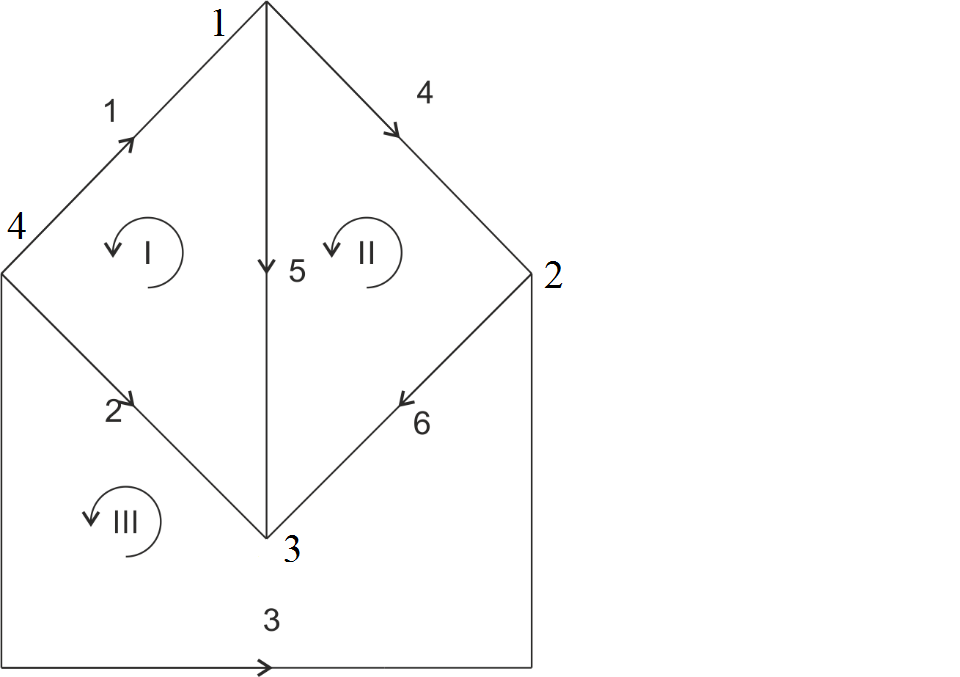
Рис.1.6 Направленный граф электрической цепи для схемы замещения, приведенной на Рис. 1.5
Направленный граф характеризует конфигурацию – геометрический образ схемы. Для аналитического представления графа должны быть пронумерованы узлы, ветви, независимые контуры и выбрано направление обходов этих контуров. В рассматриваемой схеме выбирается балансирующий узел. Геометрию графа можно записать в алгебраической форме с помощью двух матриц соединений или инциденций. 1.5.2 Первая матрица соединений (инциденций) М или матрица соединений ветвей в узлах Онапредставляет собой таблицу, строки которой отвечают узлам направленного графа электрической сети, а столбцы — ветвям.
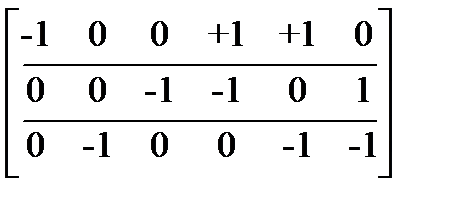
При составлении матрицы М балансирующий узел опускается. Каждая строка матрицы М отвечает одному узлу, а каждый столбец – одной из ветвей. Элементы матрицы М могут принимать одно из 3-х значений: +1 – если ветвь j выходит из узла i, т.е. узел i является началом ветви j; mij = -1 – если ветвь j входит в узел i, т.е. узел i является концом ветви j; 0 – если ветвь j не связана с узлом i. Первый закон Кирхгофа в матричной форме
Найдем произведение первой матрицы соединений М и столбцевой матрицы токов в ветвях.
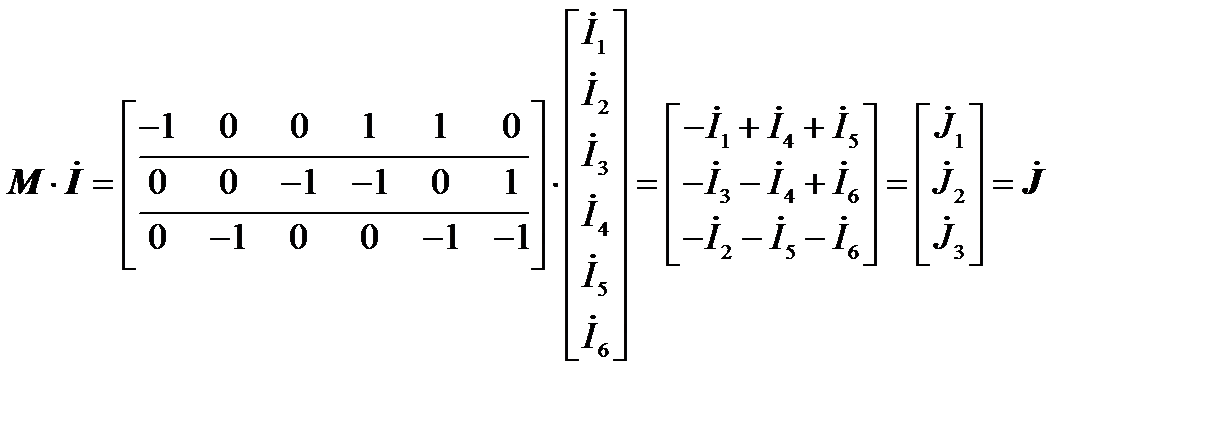
Столбцевая матрица задающих токов Сопоставив алгебраические суммы токов в строках матрицы произведения, видим, что они равны задающим токам в соответствующих узлах (см. выражения в начале п. 1.5). Первый закон Кирхгофа в матричной форме формулируется так: произведение первой матрицы соединений и матрицы – столбца токов ветвей равно матрице – столбцу задающих токов. Первый закон Кирхгофа в матричной компактной форме:
Матрица соединений (инциденций) ребра-пути Н. Это матрица, строки которой соответствуют ребрам, а столбцы путям от корня графа (базисного узла) к узлам, где подключены нагрузки. Элементы матрицы H — hij могут принимать два значения: 1 — если ветвь i входит в путь j и 0 — если ветвь i не входит в путь j. Так, для разомкнутой сети, приведенной на Рис 1.7, матрица ребра – пути имеет вид
пути Пути от базисного узла к узлам с нагрузками
Матрицу H используют при определении в схеме токораспределения. По известным токам нагрузки в узлах можно рассчитать токи в ветвях, используя выражение
Здесь
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 353; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.197.120 (0.008 с.) |

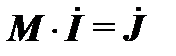 . (1.2)
. (1.2)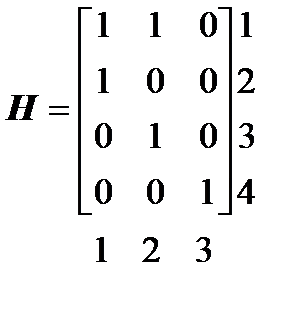 ветви (ребра) (1.3)
ветви (ребра) (1.3)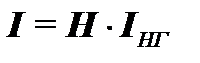 (1.4)
(1.4)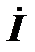 — матрица-столбец токов ветвей.
— матрица-столбец токов ветвей.


