
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Второй закон Кирхгофа в матричной форме
Число независимых контуров для схемы любой конфигурации определяется из выражения:
где m - число ветвей, n - число независимых узлов, Согласно второму закону Кирхгофа, сумма падений напряжений в сопротивлениях ветвей, составляющих независимые контуры, должна быть равна алгебраической сумме ЭДС, входящих в соответствующий контур. Для схемы замещения Рис 1.5, задавшись направлениями обхода контуров, показанными на риунке, имеем: Обозначим:
Тогда уравнения для независимых контуров согласно II закону Кирхгофа примут вид:
Вторая матрица соединений (инциденций) N, или матрица соединений ветвей в независимые контуры. Она представляет собой таблицу, строки которой отвечают независимым контурам, а столбцы — ребрам (ветвям) направленного графа. Элементы матрицы N в соответствии с принятыми направлениями обхода контуров могут принимать одно из 3-х значений: +1 – если ветвь j входит в контур i, и направление ветви j совпадает с направлением обхода контура i; nij = -1 – если ветвь j входит в контур i, и направление ветви j не совпадает с направлением обхода контура i; 0 – если ветвь j не входит в контур i. Для направленного графа Рис.5.1 получаем вторую матрицу соединений в виде
ветви Совокупность двух матриц инциденций – полное однозначное описание направленного графа схемы, т.е. можно составить направленный граф, имея обе матрицы. Это алгебраическая запись геометрического образа сети. Для схемы замещения Рис 1.5 найдем произведение второй матрицы соединений N на столбцевую матрицу падений напряжения в сопротивлениях ветвей.
В компактной форме
- первая форма второго закона Кирхгофа в матричном виде. Падения напряжения в сопротивлениях ветвей зависят от токов и сопротивлений этих ветвей. Аналитически эту зависимость можно записать в матричной форме с помощью матрицы сопротивлений ветвей. Эта матрица имеет квадратную форму, её строки и столбцы отвечают ветвям рассматриваемой схемы. Сопротивления ветвей располагаются по главной диагонали этой матрицы. Если же в схеме имеются ветви, связанные магнитным потоком взаимоиндукции, то матрица сопротивлений ветвей должна содержать сопротивления взаимоиндукции на пересечении строк и столбцов, отвечающих магнитосвязанным ветвям. В нашей схеме взаимоиндукция не учитывается, поэтому получим диагональную матрицу.
ветви Произведение матрицы сопротивлений в ветвях на матрицу токов ветвей позволяет получить матрицу падений напряжения в сопротивлениях ветвей.
В компактной форме:
После подстановки этого выражения в (1.6) получаем вторую (основную) форму второго закона Кирхгофа в матричном виде.
Если найти произведение второй матрицы соединений N на столбцевую матрицу ЭДС ветвей Е, то получим матрицу, в каждой строке которой будет алгебраическая сумма ЭДС, входящих в один независимый контур, аналогично тому, как произведение матриц
После подстановки этого выражения в правую часть (1.7) получаем третью форму второго закона Кирхгофа в матричном виде:
Закон Ома в матричной форме
Из третьей формы записи второго закона Кирхгофа имеем
или
Обозначим в (1.9) В результате получаем четвертую форму второго закона Кирхгофа
Произведение двух матриц в (1.9) равно нулю, но это не значит, что одна из матриц нулевая. Матрица
Если считать, что это не матричная форма записи, то получаем закон Ома для конкретной ветви, например, ветви между узлами 4 и 1 схемы замещения, приведенной на Рис 1.5. Под напряжением ветви будем понимать разность потенциалов узла начала ветви и узла её конца
Определить, насколько потенциал точки 4 выше потенциала точки 1 можно, рассматривая схему замещения ветви
Сопоставляя это выражение с (1.12), видим, что последнее представляет матричную запись закона Ома. Закон Ома – частный случай закона Кирхгофа для части контура, т.е. для ветви. Таким образом, закон Ома в матричной форме имеет вид:
|
|||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 434; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.36.141 (0.009 с.) |
 ,
, - число независимых контуров.
- число независимых контуров. .
. - падение напряжения в сопротивлении ветви j;
- падение напряжения в сопротивлении ветви j; -контурная ЭДС первого контура;
-контурная ЭДС первого контура; - контурная ЭДС i –го контура.
- контурная ЭДС i –го контура. .
. (1.5)
(1.5)

 BZ = E K (1.6)
BZ = E K (1.6) ветви
ветви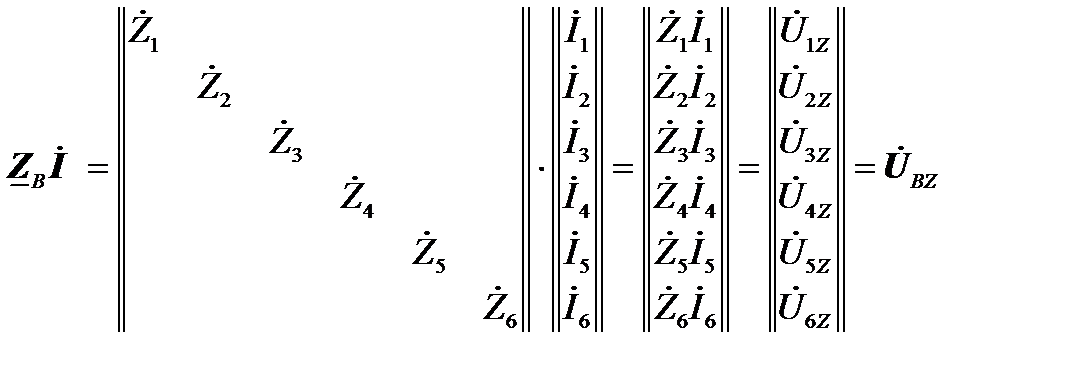 .
. .
. . (1.7)
. (1.7) и
и  определило матрицу суммы падений напряжения в ветвях этих контуров. Следовательно:
определило матрицу суммы падений напряжения в ветвях этих контуров. Следовательно: .
.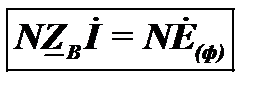 (1.8)
(1.8) ,
, . (1.9)
. (1.9) . (1.10)
. (1.10) . (1.11)
. (1.11) не равна нулю, с другой стороны —
не равна нулю, с другой стороны —  это матрица напряжений ветвей, в общем случае содержащих ЭДС, т.е. матрица напряжений ветвей.
это матрица напряжений ветвей, в общем случае содержащих ЭДС, т.е. матрица напряжений ветвей. или
или  . (1.12)
. (1.12) .
.
 .
. (1.13)
(1.13)


