
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнерия установившегося режима системы электроснабжения в матричной формеСтр 1 из 9Следующая ⇒
УРАВНЕРИЯ УСТАНОВИВШЕГОСЯ РЕЖИМА СИСТЕМЫ ЭЛЕКТРОСНАБЖЕНИЯ В МАТРИЧНОЙ ФОРМЕ Схемы замещения системы
Расчеты установившихся режимов СЭС выполняются применительно к их схемам замещения. Схемы замещения являются своего рода математическим инструментом инженера, поскольку на их основе создается математическая модель системы. Схема замещения – это совокупность элементов электрической цепи: источников ЭДС, источников тока; активных, индуктивных и емкостных сопротивлений. Чтобы получить схему замещения системы, каждый её элемент: линия, трансформатор, генератор, нагрузка — представляются своей схемой замещения. Схемы замещения отдельных элементов соединяются между собой в той же последовательности, что и в реальной схеме системы, т.о. схема замещения системы для расчета установившегося режима представляет собой электрическую цепь, и расчет установившегося режима сводится к расчету электрической цепи методами, известными из курса ТОЭ: законов Кирхгофа, узловых напряжений, контурных токов, другими методами. Однако имеются особенности и трудности, рассматриваемые ниже. В курсе рассматриваются расчеты симметричных установившихся режимов (есть еще несимметричные) системы трехфазного синусоидального переменного тока. В этом случае параметры режима и параметры системы выражаются комплексными числами. При этом схемы замещения составляются на одну фазу с нейтралью. Но при расчетах режима рассчитывают: · мощность · фазный ток · междуфазное (линейное) напряжение
Существуют различные виды схем замещения системы, различающиеся способами представления в них генераторов и нагрузок. Схема замещения системы представляет собой нелинейную электрическую цепь. Математическим описанием установившегося режима электрической системы являются уравнения состояния нелинейной электрической цепи. Важная проблема при составлении схем замещения состоит в необходимости учета того, что электрическая система содержит сети различных напряжений. Способы представления генераторных и нагрузочных узлов в схемах замещения при расчетах установившихся режимов даны таблице.
Выбор варианта схемы замещения определяется целями расчета и исходными данными. При расчетах установившихся режимов чаще всего предпочтение отдают второму способу, когда генераторы электростанций и нагрузки подстанций представляются задающими токами, поскольку схемы замещения содержат в этом случае меньшее число ветвей и контуров.
Закон Ома в матричной форме
Из третьей формы записи второго закона Кирхгофа имеем
или
Обозначим в (1.9) В результате получаем четвертую форму второго закона Кирхгофа
Произведение двух матриц в (1.9) равно нулю, но это не значит, что одна из матриц нулевая. Матрица
Если считать, что это не матричная форма записи, то получаем закон Ома для конкретной ветви, например, ветви между узлами 4 и 1 схемы замещения, приведенной на Рис 1.5. Под напряжением ветви будем понимать разность потенциалов узла начала ветви и узла её конца
Определить, насколько потенциал точки 4 выше потенциала точки 1 можно, рассматривая схему замещения ветви
Сопоставляя это выражение с (1.12), видим, что последнее представляет матричную запись закона Ома. Закон Ома – частный случай закона Кирхгофа для части контура, т.е. для ветви.
Таким образом, закон Ома в матричной форме имеет вид:
Дерево и хорды графа Вернемся к направленному графу схемы замещения рис. 1.5.
В направленном графе удобно ветви разделить на две группы: дерево графа и хорды. 1 Рис. 10 Возможные варианты деревьев графа, показанного выше Дерево графа — это подграф, состоящий из совокупности минимального числа ветвей, которые соединяют все узлы. Дерево графа — это подграф, который не содержит замкнутых контуров. На рис.10.1 ветви 1,2,3 составляют дерево графа, остальные ветви называются хордами. Деревьев можно выделить много, оно не единственное, на рис 10.2 — ветви 1, 2,4 составляют другое дерево графа. Число ветвей дерева равно числу независимых узлов, а число хорд равно числу независимых контуров. Из множества деревьев выделим дерево, ветвям которого присвоены первые номера (дерево рис 10.1). Для приведенного выше графа составим первую матрицу соединений М. Проведём в ней перегородку, выделив столбцы, соответствующие ветвям дерева 1, 2, и 3. В результате матрица М может быть представлена как клеточная матрица – строка, элементы которой — матрицы
1 2 3 4 5 6 Ветви дерева хорды
Заметим, что матрица Метод контурных токов в программных комплексах для расчетов установившихся режимов используется редко, из – за сложности и неоднозначности выделения независимых контуров. УРАВНЕРИЯ УСТАНОВИВШЕГОСЯ РЕЖИМА СИСТЕМЫ ЭЛЕКТРОСНАБЖЕНИЯ В МАТРИЧНОЙ ФОРМЕ
|
||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 293; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.121.160 (0.011 с.) |
 трех фаз в МВ
трех фаз в МВ  А, МВт, Мвар;
А, МВт, Мвар; в кА;
в кА; ,
,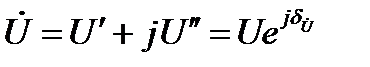 в кВ, а фазы в градусах или радианах.
в кВ, а фазы в градусах или радианах.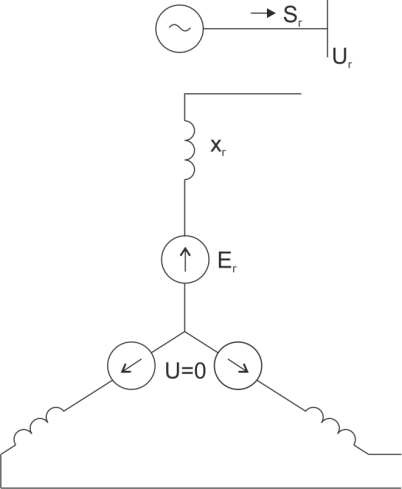 Генератор вводится в схему замещения источником ЭДС и индуктивным сопротивлением, вид которых определяется типом АРВ.
Е гф x г
Генератор вводится в схему замещения источником ЭДС и индуктивным сопротивлением, вид которых определяется типом АРВ.
Е гф x г
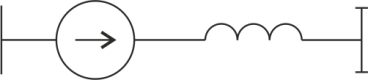
 Из треугольника сопротивлений:
Из треугольника сопротивлений:
 (1)
(1)

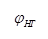

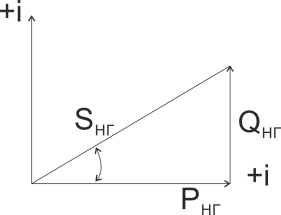
 Тогда согласно (1)
Тогда согласно (1)

 Это нелинейное сопротивление, т.к. зависит от квадрата неизвестного напряжения.
Второй способ — параллельно включенные проводимости.
Это нелинейное сопротивление, т.к. зависит от квадрата неизвестного напряжения.
Второй способ — параллельно включенные проводимости.


 ,
S Г со знаком «+».
,
S Г со знаком «+».


 — более простое обозначение задающего тока.
— более простое обозначение задающего тока.
 Нагрузка также представляется задающим током
Нагрузка также представляется задающим током
 Для нагрузочных узлов
Для нагрузочных узлов  вводится со знаком «-». Проще:
вводится со знаком «-». Проще:


 ,
, . (1.9)
. (1.9) . (1.10)
. (1.10) . (1.11)
. (1.11) не равна нулю, с другой стороны —
не равна нулю, с другой стороны —  это матрица напряжений ветвей, в общем случае содержащих ЭДС, т.е. матрица напряжений ветвей.
это матрица напряжений ветвей, в общем случае содержащих ЭДС, т.е. матрица напряжений ветвей. или
или  . (1.12)
. (1.12) .
.
 .
. (1.13)
(1.13)
 2
2 
 и
и  .
. (1.27)
(1.27) фигурирует в контурном уравнении (1.25) и в выражении для токов ветвей (1.26).
фигурирует в контурном уравнении (1.25) и в выражении для токов ветвей (1.26).


