
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рассуждения в терминах интерваловСтр 1 из 6Следующая ⇒
Каждый из нас с детства знаком с настольными играми. Основным их элементом является игральная доска, которая разбита на ячейки, соединенные тем или иным образом путями. Играющие кидают кость и из той ячейки, где они находятся, в зависимости от выпавшего числа очков переходят в ту или иную ячейку. При этом можно попасть в "хорошую" ячейку, которая расположена близко от целевой ячейки, но можно и в "плохую", из которой бросавший кость может быть переведен назад и окажется от цели дальше, чем был перед бросанием кости. Добравшись до цели раньше других выигрывает. Спектр таких игр велик: переходы из ячейки зависят от встречающихся в ячейках различных препятствий и противников, которые не только могут отбросить играющего назад, но и вообще вывести его из игры, противники имеют возможности сами перемещаться по ячейкам в ответ на ход бросающего кости и т. д. Рассмотрим простой пример среды такого типа, называемой средой чудовища. Среда имеет число ячеек, равное 4´4, расположенных по вертикали и горизонтали. Каждая внутренняя ячейка имеет четыре соседних, крайние ячейки могут не иметь соседних ячеек с одной или двух сторон. Агент, который выступает в роли единственного играющего, может переходить в одну из соседних ячеек. В одной из ячеек находится чудовище. Чудовище издает зловоние, которое распространяется на соседние ему ячейки. В одной из ячеек лежит золото, которое блестит. Кроме того, в ячейках могут быть бездонные ямы. В ячейках, соседних ячейками с ямами, ощущается сквозняк. Задача агента, стартуя в ячейке (1,1), добраться до ячейки с золотом, взять его и благополучно вернуться назад. Исходное состояние среды чудовища соответствует рис...., где буквы в ячейках обозначают следующее: Ч - чудовище, З - золото, С - сквозняк, Б - блеск, Я - яма, Н - агент. Сопоставим каждую ячейку
Естественно, такая интерпретация переменных означает, что только одна из них может быть истинна. Понятно, что суммарное число переменных равно 10´16=160, и набор значений всех переменных целиком задает значение среды чудовища. Так, например, начальное состояние среды, которое показано на рис...., определяется набором значений этих переменных, в котором 17 переменных истинны: К счастью, в реальных задачах чаще всего, во-первых, нет необходимости знать значения всех переменных, а во-вторых, агент, зачастую, и не может их знать. В нашем примере агент может воспринимать значения только тех переменных, которые относятся к ячейке, в которой он находится (т.е. имеет индекс, который совпадает с индексом ячейки местонахождения агента). При этом восприятие агента определяются следующими факторами. В ячейке, где находится чудовище, и в соседних ей ячейках агент ощущает зловоние чудовища. В ячейках, соседних ячейке, в которой находится яма, агент ощущает сквозняк. В ячейке, где находится золото, агент видит яркий блеск. Агент всегда стоит лицом к одной из соседних ячеек и может совершать одно из следующих действий:
а)поворот к ячейке, в которой нет ни чудовища, ни ямы. Сопоставим это действие с переменной б)переход в соседнюю ячейку, к которой агент стоит лицом. Сопоставим это действие с логической переменной в)изъятие золота, если агент достиг ячейки, где оно находится. Это действие сопоставим с логической переменной Теперь мы имеем достаточно полное представление о среде чудовища и цели агента и можем перейти к формальной постановке задачи. Интервальная постановка задачи. В начальном состоянии, показанном на рис..., агент находится в ячейке (1,1) и стоит лицом к ячейке (1,2) (лицом на север). Это означает истинность формулы
В левую часть этой импликации, которая является в данном случае конъюнкцией, а в общем случае любой формулой, включены не все переменные, а только часть из них, необходимая для принятия решения. В частности, в неё включены переменная Это правило задает условие допустимости совершения действия. Действие может быть и не совершенно. Но если оно совершилось, то среда перейдет в какое-нибудь другое состояние. Этот переход задается формулой
Логически любая элементарная конъюнкция эквивалентна дизъюнкции всех конституент (совершенной дизъюнктивной нормальной форме), в которой существенные переменные имеют одно и тоже значение, которое совпадает с их значением в рассматриваемой конъюнкции, а несущественные переменные пробегают все наборы значений. Множество всех полных состояний среды, каждое из которых соответствует одной из конституент совершенной нормальной формы, полученной по данной элементарной конъюнкции, называется интервалом. Используя интервалы, можно перейти от рассуждения в терминах конституент, представляющих состояния среды, к рассуждениям в терминах элементарных конъюнкций, которые представляют интервалы среды. Формулы логики высказываний, в которых используются элементарные конъюнкции, представляющие интервалы, будем называть интервальными формами. Постановка задачи теперь состоит из следующих шагов. Задание интервальных форм, которые определяют начальные интервалы среды. Задание в интервальной форме множества импликаций (правил), которые определяют условия местонахождения тех или иных объектов в ячейках среды в зависимости от восприятий агента. Задание в интервальной форме множества импликаций, которые определяют допустимые переходы между ячейками при совершении агентом действия перехода в зависимости от восприятий. Задание интервальных форм, определяющих целевые интервалы. Сформулируем теперь на основании сказанного задачу для среды чудовища полностью. Формулы, определяющие начальные интервалы. В нашем случае начальное состояние можно представить следующей конституентой, которая содержит все 160 переменных и определяет тем самым одно начальное состояние:
Агент не знает всех значений переменных, входящих в эту конституенту. Согласно его восприятию, он знает, что находится в ячейке (1,1) и стоит лицом на север, а также не ощущает в этой ячейке зловония и сквозняка. Таким образом, начальная совокупность интервалов, определяемая восприятием агента задается формулой
Формулы, определяющие местонахождения объектов среды. Если в какой-либо ячейке
Для крайних ячеек вследствие отсутствия части соседних правая часть подобных формул может не содержать каких-либо конъюнкций. Так, для
Для ячеек (1,2) и (2,1) имеем формулы
Понятно, что число формул (7.4) равно 32. Полезным могут оказаться также знания о наличии чудовища или ямы в ячейках, соседних ячейке
При
Число таких формул равно 16. Формулы, определяющие условия выполнения агентом действий. Для того чтобы достичь цели, агент должен совершать действия, которые бы привели его к этой цели. В случае среды кота, рассмотренной ранее, предполагалось, что кот может совершать одно из действий в любом состоянии и в любом порядке. Такое поведение агента в среде чудовища неприемлемо, поскольку среда небезопасна, и необходимо знать, в зависимости от обстановки, когда и какие действия можно совершать. Для среды чудовища были введены три действия: действие перехода в одну из соседних ячеек, действие по изъятию золота и действие по повороту к ячейке, в которой нет ни чудовища, ни ямы. Агент может перейти в соседнюю ячейку, если там его не подстерегает опасность в виде чудовища или ямы. Поэтому общий вид импликаций, определяющих возможность совершения действия по переходу в соседнюю ячейку, является следующим
Число таких формул равно 64. Соответственно, возможные изменения интервалов (состояний среды), которые осуществляются в результате действия, связанного с переходом, задаются формулами
Формулы, которые определяют условия выполнения действий по изъятию золота, имеют вид
и их число равно 16. Формулы, которые определяют условия возможного выполнения действия поворота агента, введем исходя из следующих соображений. Если агент стоит лицом к какой-либо ячейке и в результате своих рассуждений пришел к выводу, что в этой ячейке может быть чудовище или яма, то он поворачивается к той ячейке, в которой нет ни ямы, ни чудовища (предполагается, что такая ячейка существует). Таким образом формулы, регламентирующие возможность выполнения действия поворота направо, лицом к ячейке, в которой нет ни чудовища, ни ямы, если агент перед этим находился в ячейке
Если же агент находится в ячейке
Формулы, определяющие множество допустимых переходов. Агент может перейти из ячейки
Если действие поворота выполняется в соответствии с формулой (7.10), то импликация, определяющая местоположение и ориентацию агента, будет следующая
Формулы (7.11) и (7.12) предопределяют результат выполнения действия поворота по ходу часовой стрелки при наличии чудовища или ямы в ячейке, к которой агент стоит лицом. Агент может совершать действие поворота и против часовой стрелки в соответствии, например, с формулами типа
В том случае, когда ячейка не имеет какой-либо соседней, соответствующие условия и результат поворота модифицируются таким образом, чтобы учесть отсутствие соседних ячеек. Формулы целевых интервалов. Ограничим решение задачи нахождением золота. Агент не знает, в какой ячейке находится золото. Только попав в неё, он по блеску может определить, что оно в ней находится. Поэтому стратегией агента является обследование всех ячеек, в которые он может попасть и не погибнуть. Если ему удастся, блуждая таким образом добраться до ячейки (2,3), то он увидит блеск и обнаружит там золото. Будем полагать в настоящем примере, что целью агента является совершение действия по взятию золота, т.е. его цель С учетом того, что агент способен к восприятию сквозняка или зловония только в ячейке, в которой он находится, а среда чудовища является статической (местоположение чудовища и ям не изменяется), то для конкретных значений
Например,
Правило, которое задает условие совершения действия
Решение задачи. Рассмотрим вывод, который приводит к решению задачи нахождения агентом золота в среде чудовища. Начальный интервал задается формулой (7.3). Запишем эту формулу
Используя правило исключения конъюнкта, по этой формуле агент может заключить, что истинны формулы
Теперь агент может воспользоваться формулами (7.4), которые определяют условия местонахождения объектов среды и правилом модус поненс. Напомним их
Модус поненс. Из истинности условия импликации и истинности самой импликации следует истинность следствия импликации
Результат применения этих выражений
заключаем, что истинны формулы
Затем агент может воспользоваться правилом исключения конъюнкта, получая в результате истинные формулы
которые означают, что чудовища и ям нет в ячейках, соседних ячейке (1,1). Далее агент может воспользоваться первой формулой из числа (7.6) и правилом модус поненс
заключая, что формула
агент может установить истинность формулы Применяя формулы (7.4), правило модус поненс и правило исключения, агент устанавливает, что в ячейке (2,2) нет ямы (истинна
Используя формулы (7.5) и правило модус поненс
агент получает истинную формулу
которая означает, что чудовище может находиться в одной из ячеек (1,1), (2,2) или (1,3). Но согласно начальным условиям задачи, чудовища и ям нет в ячейке (1,1), т.е. истинны формулы
Следовательно, чудовище может находиться в одной из ячеек (2,2) или (1,3), что формально выводится с использованием правила простой резолюции
Далее на основании следующего варианта правила (7.9), т.е.
имеем
агент приходит к выводу, что у него есть единственная возможность повернуться в ячейке (1,2), что он и делает на основании следующего варианта правила, т.е.
Тем самым
Затем агент устанавливает возможность выполнения действия перехода и возвращается в ячейку (1,1) на основании правил типа
Оказавшись вновь в ячейке (1,1), агент последовательно устанавливает возможность поворота к ячейке (2,1), совершает этот поворот, устанавливает возможность перехода в эту ячейку и совершает его. Все это он делает на основании следующих правил, аналогичных по типу уже рассмотренным
Очутившись в ячейке (2,1), агент ощущает сквозняк и отсутствие зловония на основании правил типа
Так как зловония в ячейке (2.1) нет (
и правила модус поненс и исключение конъюнкта, заключает, что чудовища нет в ячейке (2,2) (
правило модус поненс и простую резолюцию, заключает, что в ячейке (3,1), к которой он стоит лицом, имеется яма (
а затем правил (7.6), (7.7)
агент сначала совершает поворот в сторону ячейки (2,2), а затем переходит в неё. В ячейке (2,2) на основании формул
он обнаруживает, что в ней нет ни зловония, ни сквозняка (истинны формулы Далее по формулам (7.4), правил модус поненс и исключением конъюнкта он устанавливает, что чудовища и ямы в ячейке (2,3) также нет (истинны формулы
После этого агент может воспользоваться одной из формул типа (7.6), одной из формул типа (7.7) и правилом модус поненс для перехода в ячейку (2,3)
В результате агент оказывается в ячейке (2,3) (истинна
Число формул в логике высказываний, требуемых для представления знаний. Нетрудно заметить, что число формул, которые требуются для постановки задачи, растет довольно быстро, хотя среда чудовища имеет всего 16 ячеек и все её объекты, кроме агента, не изменяют своего местоположения. Так, число формул типа (7.4) равно 32, (7.5) - 16, (7.6) - 64, (7.7) - 16, (7.8) - 16, (7.9) - 128, (7.10) - 16, (7.11) - 128, (7.12) - 16, (7.13) - 32, (7.14) - 32, что в сумме составляет 496. В случае более сложной среды необходимо представить все возможные изменения местоположения других объектов, например, чудовища, в ответ на действия агента и для действия каждого такого объекта предусмотреть свои формулы. Занижая оценку, будем полагать, что число формул в среде с
ЛОГИКА ПРЕДИКАТОВ Ранее было показано, каким образом логику высказываний, можно использовать для представления знаний и логических рассуждений. Однако выразительные возможности логики высказываний невысоки. Требуется слишком много формул логики высказываний для описания даже простых сред. Например, в случае простой среды чудовища для того, чтобы указать факт наличия или отсутствия любого объекта (чудовища, агента, ям, золота) в какой-либо ячейке среды, пришлось ввести для каждого объекта множество логических переменных, число которых совпадает с числом ячеек среды, и сопоставить каждое местонахождение объекта в какой-либо ячейке с координатами Здесь мы изучим логику предикатов первого порядка, называя её в дальнейшем просто логикой предикатов, которая существенно более выразительна, чем логика высказываний, и позволяет представлять знаний о среде гораздо более компактно. Выразительность логики предикатов является следствием её основополагающей идеи, которая заключается во взаимно-однозначном сопоставлении каждого уникального (не совпадающего ни с каким другим) объектом среды с индивидуальной объектной константой, которая обозначается именем (названием) объекта, а класс однотипных по каким-либо свойствам объектов - с объектной переменной, значением которой являются объектные константы. Объектные константы и переменные в литературе часто называют индивидными, или предметными. Предикатом называют высказывательную функцию, определенную на множестве наборов значений объектных переменных. Эта функция может принимать только два значения: Истина (И) и Ложь (Л), называемые истинностными значениями. Отношения объектов среды представляются на языке логики предикатов, как и на языке логики высказываний, в виде определенных предложений (высказываний, формул логики предикатов), которые используют объектные переменные и объектные константы, а также ряд других конструкций, включая уже известные связи и скобки. Рассмотрим подробнее язык логики предикатов. Синтаксис и семантика. Синтаксис логики предикатов с использованием метаязыка Бэкуса-Наура приведен ниже. Рассмотрим семантику всех синтаксических конструкций, приведенных здесь. Формула ® Атом ½ Предложение ½ Предложение Связка Предложение ½ Квантор (Переменная,...,Переменная) Предложение ½Ø Предложение ½ (Предложение), Атом ® Предикатный символ (Терм,...,Терм) ½ Терм=Терм, Терм ® Функциональный символ (Терм,...,Терм) ½ Константа ½ Переменная Связка ® Квантор ® "½$, Константа ® Строка символов, начинающаяся с прописной буквы, Переменная ® Строка символов, со строчной буквы, Предикатный символ ® Строка символов, со строчной буквы, Функциональный символ ® Строка символов, со строчной буквы. Рис. 8.1.
Объектные переменные. Объектные переменные или просто переменные обозначаются строкой символов, которая начинается со строчной буквы и записывается курсивом. Областью значений каждой переменной является множество констант, в общем случае даже бесконечное. Как это область значений очерчивается, будет ясно из дальнейшего. Функции. Для того чтобы задать такие отношения между объектами, когда в точности один объект соответствует множеству других объектов используют функции. Например, если объектами являются двоичные цифры 0 и 1 и десятичные цифры 0,1,...,9, то любому набору из трех двоичных цифр, который представляет двоичное число, можно однозначно сопоставить десятичную цифру. Если двоичные цифры сопоставить с переменными преобразование_2_в_10 Выражение преобразование_2_в_10 называют функциональным символом. Так при Объектные константы. Каждая объектная константа, называемая в дальнейшем, если это не вызывает путаницы, просто константой, взаимно однозначно сопоставляется в процессе интерпретации с каким-либо одним объектом среды. Константа обозначается строкой символов, которая начинается с прописной буквы, и, чаще всего, эта строка символов совпадает с именем или наименованием объекта и записывается курсивом, например, Владимир, Чудовище, Кот и т. д. Термы. Константы, переменные и функции являются термами. Выбор констант, переменных и функций для данной среды полностью является прерогативой того, кто использует логику предикатов. Предположим, например, что наша среда имеет такие объекты, как крылья и птицы, и нам известно, что "птицы имеют крылья". Спрашивается, как выразить это знание? Введем константы, которые обозначают конкретный вид птиц, например, Воробей, Синица, Соловей и константу Крылья, которая обозначает объект крылья. Введем также переменную Если, например,
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 320; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.90.131 (0.163 с.) |
 среды с шестью логическими переменными
среды с шестью логическими переменными 




 Будем полагать, что значения этих переменных истинно, если чудовище, зловоние, сквозняк, блеск, яма или агент присутствуют в соответствующей ячейке, и ложно в противном случае. Введем дополнительные логические переменные, которые характеризуют ориентацию агента на север, юг, восток и запад:
Будем полагать, что значения этих переменных истинно, если чудовище, зловоние, сквозняк, блеск, яма или агент присутствуют в соответствующей ячейке, и ложно в противном случае. Введем дополнительные логические переменные, которые характеризуют ориентацию агента на север, юг, восток и запад: 


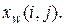 Истинное значение какого либо из них с индексом
Истинное значение какого либо из них с индексом 
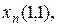

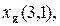
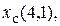

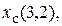


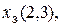

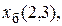



 а остальные ложны. Число таких наборов, обычно называемых полными наборами значений, или полными состояниями среды, астрономически велико и равно 2160. Конечно, далеко не во всех полных состояниях может находиться среда вследствие ограничений на значения каких-либо переменных в зависимости от значений других. Например, как уже отмечалось, никакая переменная из
а остальные ложны. Число таких наборов, обычно называемых полными наборами значений, или полными состояниями среды, астрономически велико и равно 2160. Конечно, далеко не во всех полных состояниях может находиться среда вследствие ограничений на значения каких-либо переменных в зависимости от значений других. Например, как уже отмечалось, никакая переменная из 
 с одним и тем же индексом
с одним и тем же индексом 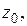 которая истинна, если действие поворота совершается, и ложна в противном случае;
которая истинна, если действие поворота совершается, и ложна в противном случае;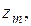 которая истинна, если действие перехода совершается, и ложна в противном случае;
которая истинна, если действие перехода совершается, и ложна в противном случае; .
. Правило для принятия агентом решения о возможности совершения действия перехода в ячейку (1,2) из ячейки (1,1) можно представить импликацией
Правило для принятия агентом решения о возможности совершения действия перехода в ячейку (1,2) из ячейки (1,1) можно представить импликацией
 которая характеризует наличие или отсутствие зловония, и переменная
которая характеризует наличие или отсутствие зловония, и переменная  которая характеризует наличие или отсутствие сквозняка. Обычно такие переменные называют существенными.
которая характеризует наличие или отсутствие сквозняка. Обычно такие переменные называют существенными.





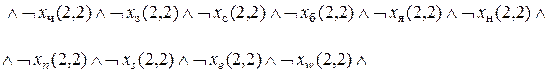









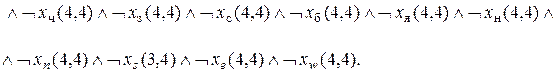



 эта формула примет вид
эта формула примет вид


 если в ней ощущается зловоние или сквозняк соответственно. Импликации, с помощью которых можно выразить эти знания, имеют следующий вид
если в ней ощущается зловоние или сквозняк соответственно. Импликации, с помощью которых можно выразить эти знания, имеют следующий вид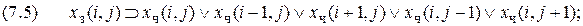

 формула(7.5) примет вид
формула(7.5) примет вид


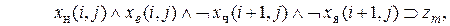






 и стоял лицом соответственно на север, восток, юг и запад, и перед ним не находились чудовища и яма, имеют вид
и стоял лицом соответственно на север, восток, юг и запад, и перед ним не находились чудовища и яма, имеют вид


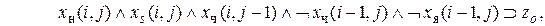


 или
или  а в ячейке
а в ячейке  нет ни чудовища, ни ямы, то можно воспользоваться формулой типа
нет ни чудовища, ни ямы, то можно воспользоваться формулой типа
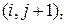


 в результате выполнения действия
в результате выполнения действия  При повороте он остается в той же ячейке. Ориентация его при этом меняется. Поэтому импликациями, определяющими местоположение и ориентацию агента после выполнения действия поворота в соответствии с формулами (7.9), будут следующие
При повороте он остается в той же ячейке. Ориентация его при этом меняется. Поэтому импликациями, определяющими местоположение и ориентацию агента после выполнения действия поворота в соответствии с формулами (7.9), будут следующие

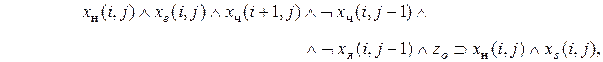








 а решением задачи должно быть нахождение последовательности действий (правил) в результате выполнения которых цель будет достигнута.
а решением задачи должно быть нахождение последовательности действий (правил) в результате выполнения которых цель будет достигнута. и
и  в соответствии с рис., по мере необходимости, будем также использовать формулы вида
в соответствии с рис., по мере необходимости, будем также использовать формулы вида








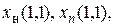
 т.е.
т.е.













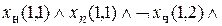

 истинная и, следовательно, он может совершить действие перехода в ячейку (1,2). Воспользовавшись этим фактом, правилом модус поненс и первой формулой из (7.7), которая принимает следующий вид
истинная и, следовательно, он может совершить действие перехода в ячейку (1,2). Воспользовавшись этим фактом, правилом модус поненс и первой формулой из (7.7), которая принимает следующий вид
 которая означает, что он после совершения действия перехода находится в ячейке (1,2) лицом на север к ячейке (1.3). Теперь процесс исследования соседних ячеек на существующие там опасности повторяется. В ячейке (1,2) агент ощущает зловоние (истинна формула
которая означает, что он после совершения действия перехода находится в ячейке (1,2) лицом на север к ячейке (1.3). Теперь процесс исследования соседних ячеек на существующие там опасности повторяется. В ячейке (1,2) агент ощущает зловоние (истинна формула 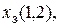 и не ощущает сквозняка (истинна формула
и не ощущает сквозняка (истинна формула 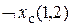 ).
).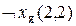 )
)
















 истинна), агент, используя формулу типа
истинна), агент, используя формулу типа
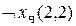 истинна). Агент ощущает сквозняк в ячейке (2,1) (
истинна). Агент ощущает сквозняк в ячейке (2,1) ( истинна), поэтому, используя формулу типа
истинна), поэтому, используя формулу типа
 истинна). Отсюда на основании правил типа
истинна). Отсюда на основании правил типа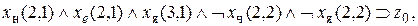






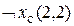 ).
).
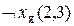 )
)



 ) и видит блеск золота (истинна
) и видит блеск золота (истинна  на основании правила
на основании правила  ). Используя формулу и правило модус поненс, агент может сделать заключение о возможности совершения действия
). Используя формулу и правило модус поненс, агент может сделать заключение о возможности совершения действия  по изъятию золота из ячейки (2,3)
по изъятию золота из ячейки (2,3)
 ячейками равно
ячейками равно 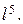 Тогда при
Тогда при  это будут числа 3125, 7776, 16807,... соответственно. Могут потребоваться также правила, которые учитывают предысторию действий агента. Все это может привести к огромному числу формул, для хранения которых потребуется такой большой объем памяти, которой может не хватить даже на современных компьютерах. Кроме того, сама постановка задачи, требующая записи такого огромного числа формул, может стать практически невыполнимой задачей. В то же время многие реальные задачи часто, несмотря на большое число переменных, могут иметь сравнительно небольшое количество формул в постановке задачи и достаточно успешно решаться с использованием логики высказываний. К числу таких задач, например, относятся задачи анализа логических схем.
это будут числа 3125, 7776, 16807,... соответственно. Могут потребоваться также правила, которые учитывают предысторию действий агента. Все это может привести к огромному числу формул, для хранения которых потребуется такой большой объем памяти, которой может не хватить даже на современных компьютерах. Кроме того, сама постановка задачи, требующая записи такого огромного числа формул, может стать практически невыполнимой задачей. В то же время многие реальные задачи часто, несмотря на большое число переменных, могут иметь сравнительно небольшое количество формул в постановке задачи и достаточно успешно решаться с использованием логики высказываний. К числу таких задач, например, относятся задачи анализа логических схем. ,
, а десятичные с переменной
а десятичные с переменной  то рассмотренное отношение между двоичными и десятичными цифрами можно представить в виде функции
то рассмотренное отношение между двоичными и десятичными цифрами можно представить в виде функции
 с помощью функции преобразование_2_в_10
с помощью функции преобразование_2_в_10  получим значение функции, равное
получим значение функции, равное  Отметим, что функция в логике предикатов не предполагает обязательного наличия какого-либо алгоритма вычисления значения функции по её аргументам. Она лишь задает с помощью констант и переменных определенное отношение между объектами, соответствующими её аргументами, и каким-то одним объектом.
Отметим, что функция в логике предикатов не предполагает обязательного наличия какого-либо алгоритма вычисления значения функции по её аргументам. Она лишь задает с помощью констант и переменных определенное отношение между объектами, соответствующими её аргументами, и каким-то одним объектом. которая обозначает все объекты, которые являются птицами: функциональный символ имеет крылья ставит во взаимно-однозначное соответствие любой птице объект крылья. Тогда функция имеет_крылья
которая обозначает все объекты, которые являются птицами: функциональный символ имеет крылья ставит во взаимно-однозначное соответствие любой птице объект крылья. Тогда функция имеет_крылья  задает отношение между объектом крылья и птицей
задает отношение между объектом крылья и птицей 
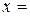 Воробей, то имеет_крылья (Воробей)= Крылья. Но это не единственная возможность выразить отношения между птицами и крыльями. Функция может не содержать аргументов, т.е. иметь только функциональный символ. Термы, которые не содержат аргументов, т.е. константы, переменные и функции без аргументов, называют элементарными термами.
Воробей, то имеет_крылья (Воробей)= Крылья. Но это не единственная возможность выразить отношения между птицами и крыльями. Функция может не содержать аргументов, т.е. иметь только функциональный символ. Термы, которые не содержат аргументов, т.е. константы, переменные и функции без аргументов, называют элементарными термами.


