
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постановка задачи для среды чудовища
В логике предикатов. Осуществим последовательно введение термов, атомов, фактов, правил и формул цели. Термы: константы Агент, Чудовище, Яма, Золото, Зловоние, Сквозняк, Блеск, 1,2,3,4; переменные переменная Атомы: находится пахнет сквозит блестит ориентация перейти повернуться взять Постановка задачи в терминах логики предикатов теперь будет выглядеть следующим образом. Факты, которые определяют начальное местоположение объектов. Начальная ситуация показана на рис., который мы повторяем.
С учетом введенных термов и атомов её (начальную) ситуацию можно представить формулой находится (Агент, 1,1) Ù ориентация (1,2) Ù Ø пахнет (1,1) Ù Ø сквозит (1,1) Правила, определяющие условия местонахождения объектов среды. Как и прежде, если в какой-либо ячейке не ощущается зловония, то в соседних ей ячейках чудовища нет. Точно так же, если в какой-либо ячейке нет сквозняка, то в соседних ячейках нет ям. Импликации, с помощью которых можно выразить эти знания, теперь приобретают следующий вид
Знания о наличии чудовища или ямы в ячейках, соседних данной ячейке, если в ней соответственно ощущается зловоние или сквозняк, можно представить в виде
Правила, определяющие условия выполнения агентом действий и допустимых переходов. Агент может перейти в соседнюю ячейку, если там его не подстерегает опасность в виде чудовища или ямы. Поэтому формулами, определяющими действия по переходу в соседнюю ячейку, являются следующие:
Формула, которая определяет условия выполнения действий по изъятию золота, имеет вид
Формулы, которые определяют условия выполнения действий поворота агента направо, имеют вид
Формулы цели. Цель агента - нахождение и изъятие золота, а решение задачи - последовательность действий, которая приводит его в ячейку, где находится золото. Поэтому формулой цели будет просто взять ИСЧИСЛЕНИЕ ПРЕДИКАТОВ Ранее было определено понятие логического исчисления. Одним из таких исчислений является классическое исчисление предикатов. Как и любое другое исчисление оно построено на использовании: алфавита (совокупности используемых символов); синтаксических правил построения формул в алфавите; аксиом (общезначимых исходных формул); правил вывода по аксиомам производных формул или теорем. Алфавит и синтаксические правила построения формул в исчислении предикатов определены выше. Множество аксиом классического исчисления предикатов определяется следующим образом: каждая аксиома классического исчисления высказываний трансформируется в аксиому классического исчисления предикатов. Эта трансформация выражается только в том, что все её логические переменные рассматриваются как предикаты, а формулы как формулы логики предикатов первого порядка.
К этому множеству аксиом, которые являются аналогом аксиом классического исчисления высказываний, добавляются две следующие аксиомы:
Общезначимость этих аксиом можно проверить с помощью таблиц истинности. Множеством правил классического исчисления предикатов является модус поненс
Классическое исчисление предикатов первого порядка не единственно. Существует множество других исчислений, построенных на основе классического, но использующих, помимо правил классического исчисления предикатов, и другие правила. В частности, выше были введены такие правила вывода в логике высказываний, как исключение конъюнкта, введение конъюнкции, исключение двойного отрицания, простая резолюция, резолюция. Эти правила справедливы и для логики предикатов, с тем только отличием, что в них используются формулы логики предикатов, а не логики высказываний. Как и в случае классического исчисления высказываний, все аксиомы классического исчисления предикатов не содержат констант. Кроме того, все предикатные символы в классическом исчислении высказываний являются абстрактными в том смысле, что любой предикатный символ в аксиомах логического исчисления может быть переименован и от этого ничего не изменится. Иными словами, аксиомы классического исчисления предикатов, как и аксиомы классического исчисления высказываний, остаются аксиомами при любой интерпретации. При использовании классического исчисления предикатов для описания свойств какоё-либо конкретной среды абстрактные предикатные символы заменяют конкретными, называемыми также индивидуальными предикатными символами. Кроме того, вводят факты, аксиомы и правила, не являющиеся аксиомами классического исчисления предикатов и зависящие от той среды, для которой осуществляется формализация постановки задачи. В результате получается некоторое новое логическое исчисление. Формулы этого исчисления по-прежнему строят по тем же правилам, показанным на рис. 8.1. С его помощью можно выводить формулы, которые нельзя получить в классическом исчислении высказываний. С практической точки зрения нас интересуют именно такие исчисления, учитывающие особенности конкретных сред. В дальнейшем ряд таких исчислений и будет рассмотрен. Чтобы отличать такие исчисления от классического исчисления логики предикатов первого порядка, назовём их неклассическими исчислениями. их числу относятся также исчисления, которые строятся не на основе логики предикатов первого порядка. Здесь же продолжим изучение неклассических исчислений, построенных на основе логики первого порядка. Пусть, например, среди множества аксиом в неклассическом исчислении для какой-либо среды имеется две аксиомы
пришлось по аксиоме
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 170; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.219.65 (0.014 с.) |
 областью значения которых являются константы 1,2,3,4;
областью значения которых являются константы 1,2,3,4; областью значений которой является множество констант Агент, Чудовище, Яма, Золото.
областью значений которой является множество констант Агент, Чудовище, Яма, Золото. , истинность которого свидетельствует, что объект
, истинность которого свидетельствует, что объект  находится в ячейке с координатами
находится в ячейке с координатами  а ложность - он там не находится;
а ложность - он там не находится; истинность которого свидетельствует, что в ячейке с координатами
истинность которого свидетельствует, что в ячейке с координатами  агент ощущает зловоние, а ложность - не ощущает;
агент ощущает зловоние, а ложность - не ощущает; агент видит блеск золота, а ложность - блеск ему не видим;
агент видит блеск золота, а ложность - блеск ему не видим; пахнет
пахнет  находится (Чудовище,
находится (Чудовище, 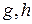 )
) 


 находится (Чудовище,
находится (Чудовище, 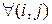 находится (Агент,
находится (Агент, 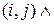 ориентация
ориентация 

 находится (Чудовище,
находится (Чудовище,  находится (Яма,
находится (Яма,  перейти,
перейти,  находится (Агент,
находится (Агент,  ориентация
ориентация 
 ориентация
ориентация  ориентация
ориентация 
 ориентация
ориентация 
 взять
взять 



 (находится (Чудовище,
(находится (Чудовище,  находится (Яма,
находится (Яма,  повернуться
повернуться 
 ориентация
ориентация  ориентация
ориентация  ориентация
ориентация  ориентация
ориентация 
 ,
, .
. , в котором
, в котором  и
и  являются формулами логики предикатов первого порядка, и два правила введения кванторов:
являются формулами логики предикатов первого порядка, и два правила введения кванторов: ,
, .
. и
и  , где
, где  переменная;
переменная;  константы;
константы;  предикатные символы. Спрашивается, можно ли на основании этих аксиом, используя правило модус поненс
предикатные символы. Спрашивается, можно ли на основании этих аксиом, используя правило модус поненс  , заключить, что формула
, заключить, что формула  истинна. Если принять
истинна. Если принять  ,
,  , то такое заключение можно было бы сделать, если бы среди исходных аксиом имелась аксиома
, то такое заключение можно было бы сделать, если бы среди исходных аксиом имелась аксиома  . Её у нас нет. Имеется только аксиома
. Её у нас нет. Имеется только аксиома  ". Когда речь идёт о всех
". Когда речь идёт о всех  хотя бы потому, что она встречается в предикате
хотя бы потому, что она встречается в предикате  ,
, можно подставить константу
можно подставить константу  ) и в результате получить аксиому
) и в результате получить аксиому 


