
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулы, которые определяют условия выполнения действий. ⇐ ПредыдущаяСтр 6 из 6
Ú переместить Формулы, определяющие условия переходов состояний среды:
Ú на
Ú свободен
Ú Ø переместить
Ú переместить Целевая формула. Целевая формула в соответствии с рис. 11.1 является конъюнкцией литералов и при прямом выводе, как и в случае использования обобщенного правила модус поненс, будет выводится для каждого литерала, входящего в её состав, раздельно
Вывод. Используя унифицированные клаузы (11.1), (13.1), которые после унификации првращаются в клаузы (13.8), (13.9) получаем резольвенту (13.10):
Используя клаузы (11.3), (13.10), получаем резольвенту
Используя эту резольвенту и унифицированную клаузу (13.4), которая после унификации превратилась в клаузу (13.12), получаем резольвенту (13.13):
Ø свободен (y),
Затем, используя клаузы (11.1), (11.3) и унифицированный резольвент (13.13), получаем резольвенту
Аналогично можем получить следующие резольвенты:
Итак, кубики A и D могут быть перемещены на стол, в результате чего кубики B и C окажутся свободными. После этого, используя клаузы (11.5), (11.6), (13.15) и клаузу (13.2), которая после унификации превращается в клаузу (13.19), получаем резольвенту (13.20)
Ú переместить (A, B),
Наконец, воспользовавшись клаузами (11.5), (11.6), (13.15), (13.20) и клаузой (13.5), которая после унификации превращается в клаузу (13.21), получим резольвенту (13.22):
Ú переместить (A, B) Ú на (A, B),
Таким образом, снова имеем истинные атомы на (A, B), на (B, Стол), на (D, Стол). Согласно правилу введения конъюнкции, вновь делаем заключение об истинности целевой формулы на (A,B) Ù на (B, Стол) Ù на (С, Стол) Ù на (D, Стол). На этом прямой вывод с использованием обобщенного правила резолюции завершён. Достоинством использования обобщенного правила резолюции для прямого вывода является способность выводить большое количество формул по сравнению с выводом на основе обобщенного правила модус поненс. В процессе вывода база знаний по-прежнему разрастается за счёт занесения в неё вновь выводимых формул. Некоторые из этих формул могут оказаться ненужными для вывода целевой формулы. Как уже отмечалось, Робинсон предложил использовать обобщенную резолюцию для создания стратегии вывода, в основе которой лежит опровержение, или доведение до противоречия. Идея этой стратегии вывода состоит в следующем. Предположим необходимо вывести истинность целевой формулы Рассмотрим стратегию обратного вывода на основе опровержения для примера с кубиками. Обратный вывод на основе опровержения и обобщенной резолюции. Как уже отмечалось, вывод истинности целевой формулы может лсуществляться по очереди литерал за литералом. Поэтому рассмотрим его только для одно литерала на (A,B) целевой формулы (13.7). Опровержение литерала на (A,B) является литерал Ø на (A,B). Обратный вывод начинается именно с этого литерала. для того чтобы можно было детально проследить процесс вывода, будем записывать на каждом шаге вывода с помощью обобщенной резолюции три формулы – две исходные и резольвенту, нумеруя по ходу вывода получаемые резольвенты, а также указывая для каждого шага используемые подстановки и подчёркивая те литералы, которые в резольвенту не попадают:
Ú переместить (A, B) Ú на ( A, B );
Ú переместить (A, B);
Ú Ø переместить ( A, B );
Ú переместить (A, B);
Ú на ( A, Стол);
Ú Ø свободен (B);
Ú Ø свободен (B);
Ú Ø свободен (B);
Преобразование произвольной формулы логики предикатов первого порядка в клаузальную форму. Применение обощенного правила резолюции требует представления формул в каузальной форме. Здесь мы покажем, с помощью каких эквивалентных преобразования любая произвольная формула логики предикатов первого порядка может быть преобразована в каузальную форму. Процедуру преобразования представим в виде отдельных шагов. Исключение импликаций. Из логики высказываний известно, что Перемещение знака отрицания (Ø) непосредственно к атомам. В клаузах отрицание допустимо только перед атомами. Поэтому используя перечисленные ниже законы Де Моргана, эквивалентности кванторов и двойного отрицания, перемещаем знак отрицания непосредственно к атомам:
Переименование переменных. Во всех формулах, в которых встречаются кванторы, использующие одни и те же связанные переменные, как, например, в формуле Перемещение кванторов влево. После предыдущего шага, в результате которого каждый квантор использует свои связанные переменные, обозначения которых не совпадают с переменными других кванторов все кванторы перемещаем влево. Так, например, простая Сколемизация. Сколемизацией называется специфический приём удаления кванторов существования. В простейшем случае – это замена формулы
Так, если имеем формулу
то здесь литерал
Распределение конъюнкций относительной дизъюнкций. Это распределение осуществляется на основе использования дистрибутивного закона
Перемещение скобок к концу и началу. На этом шаге формулы со скобками типа АВТОМАТ И СРЕДА Ранее было введено понятие формального языка логики высказываний, который используется для представления знаний о среде. С помощью этого языка осуществлялось решение задач нахождения последовательностей действий, которые ведут в целевые состояния. Таким образом, агент, который решают ту или иную задачу, фактически чаще всего имеет дело не с самой средой, а с некоторым её представлением или описанием на каком-либо языке. Поэтому он должен знать, как этот язык устроен, для этого, чтобы понимать описание, составленное на нём. Далее будут рассмотрены вопрсоы описания языков с помощью формальных грамматик и использование такого описания агентом. Стратегия поиска целевых состояний и ведущих в них последовательностей действий примера со средой кота состояла в рассмотрении всех возможных состояний и переходов из каждого состояния при выполнении каждого действия. Для решения задачи поиска золота в примере для среды чудовища применялась похожая стратегия, но с использованием не состояний, а интервалов. Отмечалось, что стратегии подобного типа неэкономны по числу шагов, используемых для поиска цели.
Описанию различных стратегий поиска будет посвящен соответствующий материал далее. Сложность поиска зависит как от объёма описания знаний о среде на том или ином языке, так и от стратегии поиска. Если описание избыточно, то часть времени поиска может расходоваться впустую на анлиз избыточной информации. Ниже будет показано также, как может быть сокращен объём описания на языке в задачах поиска целевых состояний. Конечным инициальным детерминированным автоматом называют объект, который определяется следующими шестьюми понятиями. Входной алфавит Внутренний алфавит (множество состояний автомата)
Выходной алфавит Функция перехода
Функция выходов
Начальное состояние В дальнейшем для простоты вместо длинного словосочетания "инициальный детерминированный конечный автомат" будем говорить просто "автомат". Автомат можно рассматривать как эквивалент некоторой абстрактной среды, которая имеет множество состояний Таким образом, автомат перерабатывает последовательность Последовательности действий подразделяют на допустимые и запрещенные. Допустимыми называют псоледвоательности, которые могут быть поданы на автомат, а запрещенными - последовательности, которые на автомат никогда не подаются. Условно считается, что все запрещенные последовательности ведут в одно и то же фиктивное состояние
ЯЗЫК И АВТОМАТ Множество (алфавит)
Иначе говоря, множестов последовательностей Языком называют множество последовательностей символов в каком-либо алфавите. Множества Условия полноты. Для всякой последовательности Условия непротиворечивости. Не существует ни одной пары последовательностей Условия регулярности. Любая последовательность Сокращение числа состояний. Итак полагаем, что исходным для построения автомата является язык Отношение Нетрудно показать, что отношение Множестов классов эквивалентсности можно использовать для построения автомата, реализующего множество Свойство однозначной продолжаемости. Для всякого действия Свойство связности. Для любого класса Свойство недоопределенности. Если множество допустимых последовательностей Пример сокращения числа состояний. Пусть задано следующее множество Тогда, согласно определению,
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 465; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.0.25 (0.266 с.) |
 Ø на
Ø на  Ú Ø свободен
Ú Ø свободен  Ú переместить
Ú переместить  , Стол
, Стол  ,
, Ø на
Ø на  Ú
Ú .
. Ø на
Ø на  Ø на
Ø на 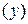 ,
, Ø на
Ø на  Ø на
Ø на 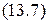 на (A,B) Ù на (B, Стол) Ù на (С, Стол) Ù на (D, Стол).
на (A,B) Ù на (B, Стол) Ù на (С, Стол) Ù на (D, Стол). на (A,С),
на (A,С), Ø на (A,С) Ú Ø свободен (A) Ú переместить (A, Стол),
Ø на (A,С) Ú Ø свободен (A) Ú переместить (A, Стол), Ø свободен (A) Ú переместить (A, Стол).
Ø свободен (A) Ú переместить (A, Стол). переместить (A, Стол).
переместить (A, Стол).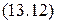 Ø на (A,y) Ú Ø свободен (A) Ú переместить (A, Стол) Ú
Ø на (A,y) Ú Ø свободен (A) Ú переместить (A, Стол) Ú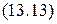 Ø на (A,y) Ú Ø свободен (A) Ú Ø свободен (y).
Ø на (A,y) Ú Ø свободен (A) Ú Ø свободен (y). свободен (C).
свободен (C). на (A, Стол),
на (A, Стол), переместить (D, Стол),
переместить (D, Стол), свободен (B),
свободен (B), на (D, Стол).
на (D, Стол). Ø на (A, Стол) Ú Ø свободен (A) Ú Ø свободен (B) Ú
Ø на (A, Стол) Ú Ø свободен (A) Ú Ø свободен (B) Ú переместить (A, B).
переместить (A, B). Ø на (A, Стол) Ú Ø свободен (A) Ú Ø свободен (B) Ú
Ø на (A, Стол) Ú Ø свободен (A) Ú Ø свободен (B) Ú на (A, B).
на (A, B). . делается опровержение этой формулы, т.е. предполагается истинным её отрицание
. делается опровержение этой формулы, т.е. предполагается истинным её отрицание  . Эта формула, которая является отрицанием целевой, заносится в базу знаний. После этого, если, начиная обратный вывод с формулы
. Эта формула, которая является отрицанием целевой, заносится в базу знаний. После этого, если, начиная обратный вывод с формулы  и
и 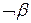 , то считается, что сделанное предположение об истинности отрицания целевой формулы ошибочно (опровергнуто) и делается заключение об истинности целевой формулы
, то считается, что сделанное предположение об истинности отрицания целевой формулы ошибочно (опровергнуто) и делается заключение об истинности целевой формулы 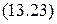 Ø на ( A,B );
Ø на ( A,B ); Ø на (A, Стол) Ú Ø свободен (A) Ú Ø свободен (B) Ú
Ø на (A, Стол) Ú Ø свободен (A) Ú Ø свободен (B) Ú Ø на (A, Стол) Ú Ø свободен (A) Ú Ø свободен (B) Ú
Ø на (A, Стол) Ú Ø свободен (A) Ú Ø свободен (B) Ú Ø на (A, Стол) Ú Ø свободен (A) Ú Ø свободен (B) Ú
Ø на (A, Стол) Ú Ø свободен (A) Ú Ø свободен (B) Ú Ø на (A, Стол) Ú Ø свободен (A) Ú Ø свободен (B) Ú
Ø на (A, Стол) Ú Ø свободен (A) Ú Ø свободен (B) Ú Ø на (A, Стол) Ú Ø свободен (A) Ú Ø свободен (B);
Ø на (A, Стол) Ú Ø свободен (A) Ú Ø свободен (B); Ø на (A, Стол) Ú Ø свободен ( A ) Ú Ø свободен (B);
Ø на (A, Стол) Ú Ø свободен ( A ) Ú Ø свободен (B); свободен ( A );
свободен ( A ); на (A, Стол) Ú Ø свободен ( B );
на (A, Стол) Ú Ø свободен ( B ); Ø на ( A, Стол) Ú Ø свободен (B);
Ø на ( A, Стол) Ú Ø свободен (B); Ø на (A, y) Ú Ø свободен (A) Ú переместить (A, Стол) Ú
Ø на (A, y) Ú Ø свободен (A) Ú переместить (A, Стол) Ú Ø на (A, y) Ú Ø свободен (A) Ú переместить (A, Стол) Ú
Ø на (A, y) Ú Ø свободен (A) Ú переместить (A, Стол) Ú Ø на (A, y) Ú Ø свободен ( A ) Ú переместить (A, Стол) Ú
Ø на (A, y) Ú Ø свободен ( A ) Ú переместить (A, Стол) Ú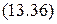 свободен ( A );
свободен ( A ); Ø на (A, y) Ú Ø переместить (A, Стол) Ú Ø свободен (B);
Ø на (A, y) Ú Ø переместить (A, Стол) Ú Ø свободен (B); Ø на (D,B) Ú Ø свободен (D) Ø переместить ( D, Стол) Ú
Ø на (D,B) Ú Ø свободен (D) Ø переместить ( D, Стол) Ú Ø на (D,B) Ú Ø свободен (D) переместить ( D, Стол);
Ø на (D,B) Ú Ø свободен (D) переместить ( D, Стол); Ø на (D,B) Ú Ø свободен (D) Ú свободен (B);
Ø на (D,B) Ú Ø свободен (D) Ú свободен (B); Ø на (D,B) Ú Ø свободен ( D ) Ú свободен (B);
Ø на (D,B) Ú Ø свободен ( D ) Ú свободен (B); свободен ( D );
свободен ( D );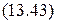 Ø на (D,B) Ú свободен (B);
Ø на (D,B) Ú свободен (B); Ø на (D,B) Ú свободен (B);
Ø на (D,B) Ú свободен (B); Ø на (D,B);
Ø на (D,B); свободен (B);
свободен (B); свободен (B);
свободен (B); Ø свободен (B);
Ø свободен (B);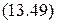 Nil.
Nil. . Поэтому на первом шаге с помощью этой формулы исключаем все импликации.
. Поэтому на первом шаге с помощью этой формулы исключаем все импликации. ,
,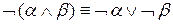 ,
, ,
, ,
,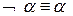 .
. , переименовываем связанные переменные таким образом, чтобы они были индивидуальными для каждого квантора. Например, для нашего примера это может быть использование переменной
, переименовываем связанные переменные таким образом, чтобы они были индивидуальными для каждого квантора. Например, для нашего примера это может быть использование переменной  вместо переменной
вместо переменной  для квантора существования. В результате получится формула
для квантора существования. В результате получится формула 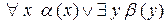 .
. после перемещения квантора влево примет вид
после перемещения квантора влево примет вид  .
. на формулу
на формулу  , где
, где  является константой, которая ранее не встречалась. В общем случае, когда переменная, которая связывается квантором существования. встречается в каком-либо литерале вместе с переменными, связанными квантором общности, приходится, чтобы избавиться от квантора общности, вводить специальную функцию, которая зависит от переменных, связанных квантором обшности, вместо переменной, связанной квантром существования.
является константой, которая ранее не встречалась. В общем случае, когда переменная, которая связывается квантором существования. встречается в каком-либо литерале вместе с переменными, связанными квантором общности, приходится, чтобы избавиться от квантора общности, вводить специальную функцию, которая зависит от переменных, связанных квантором обшности, вместо переменной, связанной квантром существования. ,
, может означать, например, наличие некоторого свойства, именуемого предикатным символом
может означать, например, наличие некоторого свойства, именуемого предикатным символом  задаёт отношение между объектами
задаёт отношение между объектами  . Объект, который обозначен переменной
. Объект, который обозначен переменной  , которая обычно называют функцией Сколема. После такой замены квантор сущестования может быть удален, а формула приобретает вид
, которая обычно называют функцией Сколема. После такой замены квантор сущестования может быть удален, а формула приобретает вид .
. .
. или
или  приводятся соответственно к виду
приводятся соответственно к виду  или
или  . После этого шага исходная формула преобразуется в нормальную конъюнктивную форму, которая является конъюнкцией дизъюнкцией литаралов. Каждая дизъюнкция литералов является клаузой.
. После этого шага исходная формула преобразуется в нормальную конъюнктивную форму, которая является конъюнкцией дизъюнкцией литаралов. Каждая дизъюнкция литералов является клаузой.
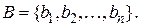

 :
:  , записываемая так же, как
, записываемая так же, как , где
, где  .
. :
:  , записываемая так же, как
, записываемая так же, как , где
, где  .
. . Обычно будем полагать, что
. Обычно будем полагать, что  .
. и начальное состояние
и начальное состояние  , агентом может быть совершено действие
, агентом может быть совершено действие  . В результате среда перейдёт в состояние
. В результате среда перейдёт в состояние  , которое определяется функцией переходов
, которое определяется функцией переходов  , то считается, что ещё никакая входная последовательность на него не была подана. Для удобства будем полагать, тем не менее, что на него была подана пустая последовательность
, то считается, что ещё никакая входная последовательность на него не была подана. Для удобства будем полагать, тем не менее, что на него была подана пустая последовательность 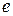 .
. в последовательности
в последовательности  ,
,  , где
, где  ,
,  ,
,  . Если на автомат была подана последовательность
. Если на автомат была подана последовательность  , то он перейдет в состояние
, то он перейдет в состояние  и т.д. Если на него была подана последовательность
и т.д. Если на него была подана последовательность  . Говорят при этом, что последовательность
. Говорят при этом, что последовательность 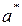 . Если она ведёт в некотрое состояние
. Если она ведёт в некотрое состояние 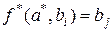 .
. и
и  . Функцию выходов можно определить не на всех состояниях. Если она не определена, то будем считать, что её значение равно
. Функцию выходов можно определить не на всех состояниях. Если она не определена, то будем считать, что её значение равно  . Если при этом
. Если при этом 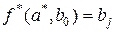 и функция выхода
и функция выхода  или
или  , то этот факт запишем
, то этот факт запишем  или
или  соответственно.
соответственно. произвольная, конечная или бесконечная последовательность допустимых действий (входная последовательность) в алфавите
произвольная, конечная или бесконечная последовательность допустимых действий (входная последовательность) в алфавите  множестов всех последовательностей
множестов всех последовательностей  ,
,  пустое действие,
пустое действие,  ,
,  функция на множестве
функция на множестве  , которая ставит в соответствие последовательностям
, которая ставит в соответствие последовательностям  элементы множества
элементы множества 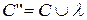 , где
, где  символ неопределенного значения, т.е.
символ неопределенного значения, т.е. 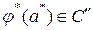 или
или 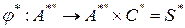 . Обозначим
. Обозначим  множество допустимых последовательностей действий агента, включая последовательность из одного пустого действия
множество допустимых последовательностей действий агента, включая последовательность из одного пустого действия 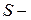 множество последовательностей
множество последовательностей  таких, что
таких, что  ,
,  ;
; 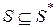 .
. таково, что оно состоит только из допустимых последовательностей действий и каждая такая последовательность ведёт в какое-либо состояние среды. Множество
таково, что оно состоит только из допустимых последовательностей действий и каждая такая последовательность ведёт в какое-либо состояние среды. Множество  получается из множества
получается из множества  (выходного символа), и наоборот, множество
(выходного символа), и наоборот, множество 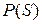 .
. являются множествами последовательностей символов и, следовательн, каждое из них можно считать языком. Говорят, что язык (множество последовательностей действий)
являются множествами последовательностей символов и, следовательн, каждое из них можно считать языком. Говорят, что язык (множество последовательностей действий)  реализуется инициальным автоматом, если любая последовательность действий
реализуется инициальным автоматом, если любая последовательность действий  , такая, что
, такая, что 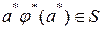 ведёт из начального состояния
ведёт из начального состояния  . О входной последовательности
. О входной последовательности  всякое её начало также принадлежит
всякое её начало также принадлежит  ,
,  , таких, что
, таких, что 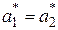 и
и  .
. . Нашей задачей является построение автомата, который реализует этот язык. Введём на множестве
. Нашей задачей является построение автомата, который реализует этот язык. Введём на множестве  отношение
отношение  , которое определяется следующим образом.
, которое определяется следующим образом.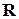 .
.  , если
, если  и
и  для всех
для всех  ,
,  .
.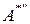 на классы эквивалентности
на классы эквивалентности 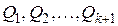 , где
, где  класс эквивалентности отношения
класс эквивалентности отношения  за счёт введения значения
за счёт введения значения  , на основании следующих свойств классов эквивалентности
, на основании следующих свойств классов эквивалентности  ,
,  , существует единственный класс
, существует единственный класс  ,
,  , такой, что и
, такой, что и  , где
, где  множество всех входных последовательностей
множество всех входных последовательностей 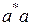 , таких, что последовательность
, таких, что последовательность  .
. , такая, что
, такая, что  ,
,  ,
, 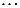 ,
,  .
.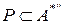 , то существует единственный класс эквивалентности
, то существует единственный класс эквивалентности  ,
, 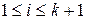 , все последовательности которого не принадлежат множеству
, все последовательности которого не принадлежат множеству  . Для определенности будем считать, что этот единственный класс последовательностей есть
. Для определенности будем считать, что этот единственный класс последовательностей есть  . Из этого свойства также следует, что пересечение класса
. Из этого свойства также следует, что пересечение класса  , а все остальные классы
, а все остальные классы  , включаются в множество
, включаются в множество  Построение автомата (обозначим его
Построение автомата (обозначим его  ), реализующего язык
), реализующего язык  отношения
отношения 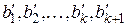 автомата
автомата  , то состояние
, то состояние  переходит
переходит  , т.е. если
, т.е. если  , где
, где  функция переходов. Функция переходов однозначна вследствие свойства однозначной продолжаемости. Функцией выходов автомата
функция переходов. Функция переходов однозначна вследствие свойства однозначной продолжаемости. Функцией выходов автомата  , где
, где 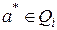 . Функция выходов автомата
. Функция выходов автомата 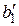 , соответствующее классу эквивалентности
, соответствующее классу эквивалентности 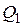 , который содержит пустую последовательность
, который содержит пустую последовательность  состояние, каждое из которых соответствует классу
состояние, каждое из которых соответствует классу 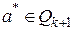 , имеет место
, имеет место  и этот класс единственный. Автомат
и этот класс единственный. Автомат  , который реализует язык
, который реализует язык  и соответственно переходов в него. Множество состояний автомата
и соответственно переходов в него. Множество состояний автомата  .
.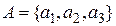 ,
,  ;
; 
 .
. .
.


