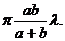Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прохождение света через плоско параллельные пластины (П.п.)
При прохождении света через плоскопараллельную пластину, луч смещается параллельно самому себе на величину Д, которая зависит от угла падения и толщины пластины. Разложение сложного света на первой преломляющей поверхности компенсируется второй поверхностью. Оптическая длина пути луча света в П. п. — nd [d — геометрическая толщина П. п., n = n(λ) — Преломления показатель её материала]. Если угол падения i луча света на П. п. отличен от 0 (см рис.), то после прохождения через пластинку этот луч, сохраняя своё направление в результате двукратного преломления на поверхностях П. п., смещается на расстояние δL, тем большее, чем больше i, d и n. При введении П. п. на пути пучка лучей, создающего Изображение оптическое точки, это изображение смещается на некоторое расстояние δl. Для параксиального пучка лучей (См. Параксиальный пучок лучей), ось которого нормальна П. п., δl = d(1 — 1/n).
Дифракция на дифракционной решётке. Формула Вульфа – Брэгга. Дифракционная решётка — оптический прибор, работающий по принципу дифракции света, представляет собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесённых на некоторую поверхность. Фронт световой волны разбивается штрихами решётки на отдельные пучки когерентного света. Эти пучки претерпевают дифракцию на штрихах и интерферируют друг с другом. Так как для разных длин волн максимумы интерференции оказываются под разными углами (определяемыми разностью хода интерферирующих лучей), то белый свет раскладывается в спектр. Для того чтобы две испускаемые волны имели одинаковую фазу и усиливали друг друга, длина их пути должна отличаться на целое число длин волн. Эту разность можно записать как пк, где и-целое число, а А,-длина волны рентгеновских лучей. Таким образом, угол отражения рентгеновских лучей должен быть связан с расстоянием d между двумя слоями атомов в кристалле соотношением (формула Вульфа – Брэгга).
Физический смысл абсолютного и относительного показателя преломления. Абсолютный показатель преломления света - отношение скорости света в вакууме к фазовой скорости света в заданной среде. Абсолютный показатель преломления света показывает изменение скорости света при переходе в вакуум. определяется как отношение синуса угла падения к синусу угла преломления луча, входящего из пустоты в данную прозрачную среду:
n = sin α/sin β = const. Относительный показатель преломления света показывает, во сколько раз замедляется скорость распространения света при переходе луча из среды одной плотности в среду другой плотности. Относительный показатель преломления равен отношению абсолютных показателей преломления: n = n2/n1, где n1 и n2 - абсолютные показатели преломления первой и второй среды. Метод зон Френеля Первую задачу, которую должен был рассмотреть Френель, выдвинув новую формулировку принципа Гюйгенса, явилась задача о прямолинейном распространении света. Френель решил ее путем рассмотрения взаимной интерференции вторичных волн, применив чрезвычайно наглядный прием, заменяющий сложные вычисления и имеющий общее значение при разборе задач о распространении волн. Метод этот получил название метода зон Френеля.
Рис. 5.2.1 Метод зон Френеля Рассмотрим действие световой волны, испущенной из точки А, в какой — либо точке наблюдения В. Согласно принципу Гюйгенса — Френеля заменим действие источника А действием воображаемых источников, расположенных на вспомогательной поверхности S. В качестве такой вспомогательной поверхности S выберем поверхность фронта волны, идущей из А (рис. 5.2.2.). Вычисления результата интерференции вторичных волн очень упрощается, если применить следующий указанный Френелем прием: для вычисления действия в точке В соединяем А с В и разбиваем поверхность S на зоны такого размера, чтобы расстояния от краев зоны до В отличались на ½ l, т.е. М1В-М0В=М2В-М1В=М3В-М2В=…= ½ l Нетрудно вычислить размеры полученных таким образом зон. Из рис. 5.2.3 получаем для первой зоны Так как l очень мало по сравнению с а или b, то
Практически ту же площадь будет иметь и каждая из всех последующих зон. Таким образом, построение Френеля разбивает поверхность сферической волны на равновеликие зоны, каждая из которых имеет площадь
Рис.5.2.3. Вычисление площади центральной зоны Френеля
Амплитуда s результирующего колебания, получающегося вследствие взаимной интерференции света, идущего к точке В от различных участков нашей сферической волны, меньше амплитуды, создаваемой действием одной центральной зоны. Таким образом действие всей волны на точку В сводится к действию ее малого участка, меньшего, чем центральная зона с площадью
Следовательно, распространение света от А до В действительно происходит так, как если бы световой пучок шел внутри очень узкого канала вдоль АВ, т.е. прямолинейно.
|
||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 1359; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.248.208 (0.006 с.) |
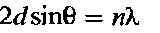


 Рис. 5.2.2. Построение зон Френеля
Рис. 5.2.2. Построение зон Френеля