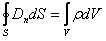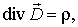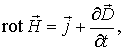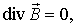Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эксперимент, показывающий воздействие силы Лоренца на заряженные частицы
Пучок электронов, движущихся по круговой траектории под воздействием магнитного поля. Свечение вызвано возбуждением атомов остаточного газа в баллоне В электроприборах Основным применением силы Лоренца (точнее, её частного случая — силы Ампера) являются электрические машины (электродвигатели и генераторы). Сила Лоренца широко используется в электронных приборах для воздействия на заряженные частицы (электроны и иногда ионы), например, в телевизионных электронно-лучевых трубках, а также в масс-спектрометрии и МГД генераторах. В ускорителях заряженных частиц Сила Лоренца также используется в ускорителях заряженных частиц, задавая орбиту, по которой движутся эти частицы.
30. Поток вектора магнитной индукции, пронизывающий площадку S - это величина, равная:
Поток вектора магнитной индукции (магнитный поток) измеряется в веберах (Вб)
Магнитный поток - величина скалярная. Поток вектора магнитной индукции (магнитный поток) равен числу линий магнитной индукции, проходящих сквозь данную поверхность. Поток вектора магнитной индукции (магнитный поток) сквозь произвольную замкнутую поверхность равен нулю:
Работа магнитного поля по перемещению контура с током. На проводнике с током в магнитном поле действуют силы, определяемые законом Ампера. Если проводник не закреплен(одна из сторон контура изготовлена в виде подвижной перемычки) то под действием силы Ампера он будет в магнитном поле перемещаться. Следовательно, магнитное поле совершает работу по перемещению проводника с током. Сила, направленная которой определяется по правилу левой руки, а значение – по закону Ампера, равна F=Ibl. Работа, совершаемая магнитным полем, равна dA=Fdx=IBldx=IBdS=IdФ, т.к ldx=dS – площадь, пересекаемая проводником при его перемещении в магнитном поле, DdS=dф- поток вектора магнитной индукции, пронизывающий эту площадь. dA=IdФ т.е работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником.
Уравнение Максвелла. Уравнения Максвелла общие уравнения для электрических и магнитных полей в покоящихся средах. Уравнения Максвелла не симметричны относительно элект и магнит полей.
Первое уравнение Максвелла – циркуляция вектора напряженности суммарного поля равна
Второе уравнение Максвелла – обобщенная теорема о циркуляции вектора Н
Еще два уравнения выражают теорему Гаусса для электрического и магнитного полей. Согласно теореме Гаусса для вектора электрической индукции D поток этого вектора через любую замкнутую поверхность S равен суммарному заряду, заключенному внутри этой замкнутой поверхности.
Это уравнение показывает, что источником электрического поля могут быть электрические заряды. Теорема Гаусса для индукции магнитного поля утверждает, что поток вектора В через любую замкнутую поверхность равен нулю.
Это уравнение указывает на замкнутость линий магнитной индукции, то есть на отсутствие источников, на которых бы эти линии начинались или оканчивались. Уравнения Максвелла в дифференциальной форме (характеризующих поле в каждой точке пространства)
Обе формы Максвелла – интегральная и дифференциальная- эквиваленты. Однако, если имеются поверхности разрыва – поверхности, на который свойства среды или полей меняются скачкообразно, то интегральная форма уравнений является более общей.
|
|||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 502; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.150.55 (0.005 с.) |



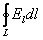 =
= 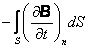 Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.
Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.
 Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами(эл токами), либо переменными электрическими полями.
Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами(эл токами), либо переменными электрическими полями. В общем случае, когда заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью ρ, то эта формула приобретает вид:
В общем случае, когда заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью ρ, то эта формула приобретает вид: