
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способ обратной угловой засечкиСодержание книги
Поиск на нашем сайте На местности находят приближенное положение К' выносимой проектной точки К (рис. 1.49). Над точкой К' устанавливают теодолит и с требуемой точностью измеряют углы β1, β2 как минимум на три опорные точки с известными координатами. По формулам обратной угловой засечки вычисляют координаты точки К' и сравнивают их с проектными значениями. По разности координат определяют величины редукций Δх, Δу или угловой Ө и линейный е элементы и смещают точку в проектное положение К.
Рис. 1.49. Способ обратной угловой засечки Для контроля на точке К измеряют углы и по ним вычисляют координаты точки К и сравнивают их с проектными. При недопустимых расхождениях измерения повторяют. Вычисление координат точки К можно выполнить по формулам:
Вычисления по этим формулам удобно выполнять по следующей схеме:
Контроль: Δх = Δх1 Δу = Δх tgα Значения к1, к3 получают из решения определителей, а к2, к4 — путём суммирования результатов умножения элементов верхней строки на лежащие под ними элементы нижней строки. Точность разбивки способом обратной угловой засечки зависит от ошибки засечки, исходных даннх, центрирования теодолита и визирных целей, фиксации выносимой точки и редуцирования. При большом расстоянии от определяемой до исходных точек наиболее сущетвенными будут влияние ошибок засечки и исходных данных. Средние квадратические ошибки координат точки К методом обратной угловой засечки:
где mβ — средняя квадратическая ошибка измерения угла. Средняя квадратическая ошибка положения определяемой точки
Если на пункте К измеряли направления способом круговых приёмов, то
где mН — средняя квадратическа ошибка направления. Входящие в формулы (1.54) — (1.56) площадь F и стороны σ1, σ2, σ3 инвертного (обращённого) треугольника 1'2'3' измеряют по схеме (рис. 1.50), на которой в произвольном масштабе по направлениям на пункты 1, 2, 3 откладывают величины ri = ρ / si, где si — расстояние от пункта К до пункта i, получают обращенный треугольник 1'2'3' со сторонами σ1, σ2, σ3. Если точки 1'2'3' лежат на одной прямой, то площадь F = 0, mx = my = M = ∞, т.е. Имеем неопределённость решения обратной угловой засечки.
Рис.1.50. Элементы инертного треугльника При β1 = 120°, β1 = 240° и расстояниях К1 ≈ К2 ≈ К3 =sср (рис. 1.49) М = 4,56 m β sср, где mβ — в сек. дуги, sср — в км, М — в мм Для приблеженных расчётов в при опредлении влияния ошибок исходных данных приведена формула
где m123 = m1=m2=m3 — ошибки в положении исходного пункта; ω123 = углу 123; τ = β2 + ω123 — 180°; bср = b12≈ b13 При sср = 1400м, bср = 2100 м, β2 = 220°, ω123 = 85°, mβ = 2", m123 = 5 мм находим
Элементы кривой Схема круговой кривой
Радиус закругления R выбирают в соответствии с условиями техники безопасности эксплуатации сооружения и рельефа. По φ и R вычисляют основные элементы круговой кривой. Тангенс (Т) – расстояние от вершины угла (ВУ) до начало кривой (НК) или конца кривой (КК):
Кривая (К) – длина дуги окружности с радиусом R от НК до КК:
Биссектриса (Б) – расстояние от ВУ до середины кривой (СК): Б Домер (Д) – разность путей по ломаной линии и дуге: Д=2Т–К За концом кривой все пикеты смещаются вперед на Д. Для того чтобы разбить круговую кривую на местности достаточно закрепить ее основные точки: начало, середину и конец. Для того чтобы закрепить НК и КК от ВУ по оси трассы откладывают Т. Для того чтобы закрепить СК, при помощи теодолита откладывают угол β/2 и в этом направлении откладывают Б. Пикетажное значение НК и КК вычисляют по формулам: НК=ВУ–Т КК=НК+К Контроль: КК=ВУ+Т–Д При больших R не достаточно только закрепить НК, СК, КК. В этом случае пользуются детальной разбивкой круговой кривой, которая выполняется, например, способом прямоугольных координат, продолженных хорд и т.д. Дальше приступают к нивелированию трассы, которое начинают с привязки трассы к реперу ГВС. Привязка заключается в проложении нивелирного хода о репера до начала трассы (ПК0). Далее нивелируют пикеты, «плюсовые» точки, поперечники, главные точки кривых. Нивелирование выполняется геометрическим способом «из середины», причем пикеты нивелируют как связующие точки (по двум сторонам реек), а остальные как промежуточные (по черной стороне). Заканчивается нивелирование привязкой трассы к реперу высотной сети.
Для вычисления координат х, у точек детальной разбивки предварительно вычисляют центральный угол θ, соответствующий заданной дуге k,
Далее, решая прямоугольный треугольник ОС1, получают:
или Аналогичным образом вычисляют координаты последующих точек, расположенных на первой половине кривой, через расстояние k по дуге кривой:
Определение положения точек 1, 2, 3,... кривой на местности сводится к откладыванию рулеткой от НК (или КК) по направлению тангенса отрезков х1, х2, х3 …, построению при помощи эккера (теодолита) перпендикуляров из концов этих отрезков и откладыванию по ним отрезков у1, у2, у3 …,
Полярный способ (способ углов) целесообразно применять на косогорах, насыпях и в полузакрытой равнинной местности. Способ базируется на положении геометрии о том, что угол с вершиной в какой-либо точке кривой, образованный касательной и секущей, равен половине соответствующего центрального угла. Как видно из рисунка, хорда Положение точек кривой на местности определяют линейно-угловыми засечками. Для этого теодолит устанавливают в точке НК (или КК) и от направления тангенса откладывают последовательно углы Недостатком способа является снижение точности детальной разбивки с увеличением числа точек, так как положение каждой последующей точки находится относительно предыдущей. Способ продолженных хорд применяют при разбивке кривых на застроенных и залесенных участках, в выемках и тоннелях. Разбивку кривой ведут с помощью мерной ленты и рулетки. По радиусу кривой R и принятой длине хорды l вычисляют длину отрезка d, называемого промежуточным перемещением.
Положение первой точки кривой находят способом прямоугольных координат; при этом значения координат х1 и у1 вычисляют по формулам (1) и (2). Закрепив на местности точку 1, на продолжении створа линии НК— 1 откладывают длину хорды l и отмечают временную точку 2'. Затем находят положение точки 2 на кривой линейной засечкой отрезками I из точки 1 и d из точки 2''. Положение остальных точек детальной разбивки до середины кривой находится аналогичным образом. Данный способ имеет тот же недостаток, что и полярный способ.
|
||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 748; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |


 (1.53)
(1.53)
 (1.54)
(1.54) (1.55)
(1.55) (1.56)
(1.56)
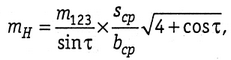

 Для расчета закругления на местности теодолита измеряют угол β, для того чтобы вычислить угол поворота трассы φ=180º–β (φ –угол между первоначальным и последующим направлением трассы)
Для расчета закругления на местности теодолита измеряют угол β, для того чтобы вычислить угол поворота трассы φ=180º–β (φ –угол между первоначальным и последующим направлением трассы)


 Способ прямоугольных координат является наиболее точным и простым; он применяется в открытой равнинной местности. В этом способе положение точек на кривой через равные промежутки k определяется прямоугольными координатами х и y; за ось абсцисс принимают линию тангенса (касательной), а за начало координат — начало (НК) или конец кривой (КК).
Способ прямоугольных координат является наиболее точным и простым; он применяется в открытой равнинной местности. В этом способе положение точек на кривой через равные промежутки k определяется прямоугольными координатами х и y; за ось абсцисс принимают линию тангенса (касательной), а за начало координат — начало (НК) или конец кривой (КК).
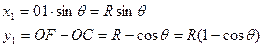

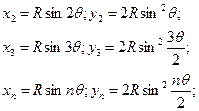
 Разбивку ведут от начала кривой (НК) до середины, а затем от конца кривой (КК) также до середины кривой (СК). Обе половины кривой должны сомкнуться в точке СК, что контролирует точность детальной разбивки. Достоинством данного способа является то, что положение каждой точки кривой определяется независимыми промерами и при переходе от одной точки к другой погрешности не накапливаются.
Разбивку ведут от начала кривой (НК) до середины, а затем от конца кривой (КК) также до середины кривой (СК). Обе половины кривой должны сомкнуться в точке СК, что контролирует точность детальной разбивки. Достоинством данного способа является то, что положение каждой точки кривой определяется независимыми промерами и при переходе от одной точки к другой погрешности не накапливаются. . Отсюда
. Отсюда 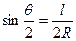 .
. и т. д. Отложив рулеткой по направлению первого визирного луча отрезок l, закрепляют на местности точку 1. Из точки1 протягивают рулетку до пересечения отрезка l со вторым визирным лучом и закрепляют точку 2 и т. д.
и т. д. Отложив рулеткой по направлению первого визирного луча отрезок l, закрепляют на местности точку 1. Из точки1 протягивают рулетку до пересечения отрезка l со вторым визирным лучом и закрепляют точку 2 и т. д. Значение величины d находят из подобия треугольников 0—1—2 и 1—2—2':
Значение величины d находят из подобия треугольников 0—1—2 и 1—2—2': отсюда
отсюда 



