
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гіперболічні функції, їх властивості .Содержание книги
Поиск на нашем сайте
Означення. Гіперболічним синусом, косинусом, тангенсом і котангенсом називаються функції, які визначаються формулами:
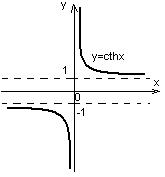
Область визначення функцій Графіки функції
За допомогою перетворень графіків основних елементарних функцій можна дістати графіки багатьох інших функцій. Якщо графік 1. 2. 3. 4. 5. 6. 7. Над функціями можна виконувати арифметичні операції додавання і віднімання Означення. Нехай функція Наприклад. Ф ункція Означення. Функція називається елементарною, якщо вона утворена з основних елементарних функцій за допомогою скінченної кількості арифметичних операцій і суперпозицій. Виділяють такі класи елементарних функцій: 1) Цілі раціональні (многочлени): 2) 3) Дробові раціональні: 4) Ірраціональні: утворюються з раціональних функцій і степеневих з дробовими показниками. 5) Трансцендентні (не є раціональними або ірраціональними):
Найпростіші властивості функцій Парність і непарність. Означення. Функція Означення. Функція називається непарною, якщо для будь – якого х з області визначення Зауваження. Графік парної функції симетричний відносно осі Періодичність. Означення. Функція Якщо Т – період функції, то періодами є також числа Приклад. 1) 2) 3) Обмеженість. Означення. Функція Значення обмеженої функції не виходять за межі відрізка Приклад. Означення. Функція Приклад. Функція Зауваження. Обмеженість функції характеризує множину значень цієї функції. Монотонність. Означення. Якщо для двох довільних різних значень 1) 2) 3) 4) Функції зростаючі, незростаючі, спадні і неспадні називаються монотонними, а функції зростаючі і спадні називаються строго монотонними. Якщо функція не є монотонною в усій області визначення, то вона може бути монотонною на деякій кількості проміжків, які не перетинаються, а в об’єднані співпадають з областю визначення. Такі проміжки називаються проміжками монотонності функції. Приклад. Функція Функції
|
||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 294; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.21.209 (0.009 с.) |

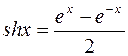


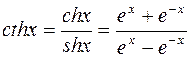
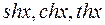 є
є  а областю визначення функції
а областю визначення функції 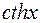 є
є 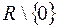 .
.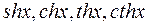 мають вигляд.
мають вигляд.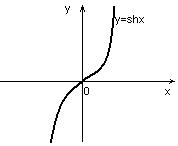


 відомий то
відомий то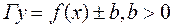 , дістанемо з
, дістанемо з  паралельним перенесенням вздовж осі
паралельним перенесенням вздовж осі  вверх (вниз) на
вверх (вниз) на 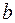 од.
од. , дістанемо з
, дістанемо з  вліво (вправо) на
вліво (вправо) на  од.
од. - збільшенням всіх ординат в
- збільшенням всіх ординат в  разів (
разів (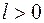 ) або зменшенням в
) або зменшенням в  разів (
разів (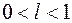 )
) - збільшенням всіх абсцис в
- збільшенням всіх абсцис в  разів
разів 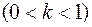 зменшенням в
зменшенням в 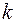 разів
разів 
 - симетрія відносно осі
- симетрія відносно осі 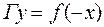 - симетрія відносно осі
- симетрія відносно осі  - всі точки графіка, що лежать нижче осі
- всі точки графіка, що лежать нижче осі  , множення
, множення 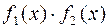 , ділення
, ділення 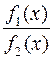
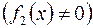 . Визначимо ще одну операцію: суперпозицію.
. Визначимо ще одну операцію: суперпозицію.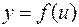 визначена на множині
визначена на множині  , а функція
, а функція 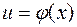 - на множені
- на множені 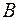 , причому для кожного
, причому для кожного 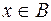 відповідне значення
відповідне значення 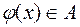 . Тоді на множені В визначена функція
. Тоді на множені В визначена функція  , яка називається складеною функцією від х, або функцією від функцій, або суперпозицією функцій
, яка називається складеною функцією від х, або функцією від функцій, або суперпозицією функцій  і
і  .
.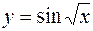 є суперпозицією двох елементарних функцій: тригонометричної
є суперпозицією двох елементарних функцій: тригонометричної 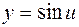 і степеневої
і степеневої  .
.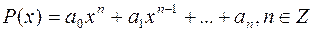 , якщо
, якщо 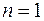 маємо лінійну функцію,
маємо лінійну функцію, 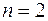 – квадратичну.
– квадратичну.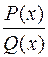 .
.
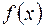 називається парною, якщо для будь – якого х з області визначення
називається парною, якщо для будь – якого х з області визначення  вона задовольняє умову
вона задовольняє умову 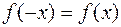

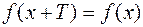 . Число Т називається періодом функції.
. Число Т називається періодом функції. ,
,  Найменший з додатних періодів, якщо він існує, називається основним.
Найменший з додатних періодів, якщо він існує, називається основним. - основний
- основний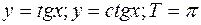 - основний
- основний - (с – стала) Т – довільне ненульове число, не існує основного періоду.
- (с – стала) Т – довільне ненульове число, не існує основного періоду. , що для всіх
, що для всіх 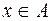 виконується нерівність
виконується нерівність 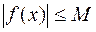 .
.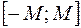 , тому її графік лежить між прямими
, тому її графік лежить між прямими 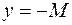 та
та 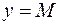 .
. обмежені на R.
обмежені на R. , що виконується нерівність
, що виконується нерівність 
 обмежена знизу прямою
обмежена знизу прямою  (віссю Ох) і необмежена зверху. Функція
(віссю Ох) і необмежена зверху. Функція  необмежена.
необмежена.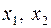 з області визначення функції
з області визначення функції 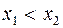 випливає, що
випливає, що , то функція називається зростаючою.
, то функція називається зростаючою. , то функція називається неспадною.
, то функція називається неспадною.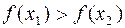 , то функція називається спадною.
, то функція називається спадною. , то функція називається незростаючою.
, то функція називається незростаючою.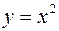 не монотонна на R, але має два проміжки монотонності: на
не монотонна на R, але має два проміжки монотонності: на  вона спадає, на
вона спадає, на 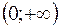 зростає.
зростає.


