
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття множини. Операції над множинами. Числові множини.Содержание книги
Поиск на нашем сайте
ЛЕКЦІЯ № 8 з навчальної дисципліни Вища математика Тема. Елементарні функції. Заняття. Функції. Границя функції. Навчальний час – 2 години. Напрямку підготовки – 6.050903 – телекомунікації Для студентів спеціальності – інформаційні мережі зв’язку Навчальна та виховна мета:
1. Студенти повинні знати теоретичні питання з теми «Функції: означення, способи задання, властивості»: основні поняття з даної теми, види елементарних функцій, властивості. 2. Студенти повинні вміти будувати графіки елементарних функцій, описувати їх властивості. 3.Розвиток мислення студентів, залучення до вивчення математики, як необхідної складової фахівця технічного університету
Київ – 20 __ План. 1. Поняття множини. Операції над множинами. Числові множини. 2. Сталі та змінні величини. Поняття функції. Способи задання функції. 3. Основні елементарні функції, їх властивості і графіки. Елементарні функції та їх класифікація. 4. Найпростіші властивості функцій. 5. Функції, задані неявно. Обернені функції. Функції, задані параметрично 6. Границя послідовності та функції. 7. Нескінченно великі та нескінченно малі величини, їх властивості. Порівняння нескінченно малих величин. 8. Основні теореми про границі. 9. Перша та друга визначні границі, наслідки. 10. Неперервність функції, точки розриву та їх класифікація.
ЛІТЕРАТУРА: 1. Барковський В.В., Барковська Н.В. Вища математика для економістів. – К.: ЦУЛ, 2002 – 401 с. 2.Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. – Москва: Наука, – 1988 – 432 с. 3.Валєєв К.Г., Джалладова І.А.Вища математика. НМП для самостійного вивчення дисципліни. – К.: КНЕУ, 2002 – 606с. 4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч 1-2. Москва.: Высшая школа, 1986. 5. Кривуца В.Г., Барковський В.В., Барковська Н.В. Вища математика. Практикум. - К.:ЦУЛ, 2003 – 536 с. 6. Овчинніков П.Ф., Яремчик Ф.П., Михайленко В.М. Вища математика. – К.: Техніка, ч.І 596 с., ч.ІІ 792 с., 2000.
Конспект лекції
Числові множини. Множина дійсних чисел. Означення. Множини, елементами яких є числа називаються числовими. Основні числові множини: - множина натуральних чисел - множина цілих чисел - множина раціональних чисел - множина дійсних чисел Між цими множинами існує зв’язок:
Сталі та змінні величини. Основні елементарні функції, їх властивості і графіки. Найпростіші властивості функцій Парність і непарність. Означення. Функція Означення. Функція називається непарною, якщо для будь – якого х з області визначення Зауваження. Графік парної функції симетричний відносно осі Періодичність. Означення. Функція Якщо Т – період функції, то періодами є також числа Приклад. 1) 2) 3) Обмеженість. Означення. Функція Значення обмеженої функції не виходять за межі відрізка Приклад. Означення. Функція Приклад. Функція Зауваження. Обмеженість функції характеризує множину значень цієї функції. Монотонність. Означення. Якщо для двох довільних різних значень 1) 2) 3) 4) Функції зростаючі, незростаючі, спадні і неспадні називаються монотонними, а функції зростаючі і спадні називаються строго монотонними. Якщо функція не є монотонною в усій області визначення, то вона може бути монотонною на деякій кількості проміжків, які не перетинаються, а в об’єднані співпадають з областю визначення. Такі проміжки називаються проміжками монотонності функції. Приклад. Функція Функції
Функції, задані неявно. Означення. Якщо функція задана рівнянням Означення. Якщо функція задана рівнянням Приклад.
Обернені функції. Означення. Функція, що ставить кожному елементу Позначення: Функція 1) областю визначення функції
2) множина значень функції
3) кожному значенню Кожна з функцій Приклад. 1. 2.
3.
Еквівалентні НМ функції. Означення. Функції Еквівалентність НМ функцій позначається так: Властивості еквівалентних НМ функцій: Теорема 1. Н Малі
Теорема 2. Сума скінченної кількості НМ функцій різних порядків еквівалентна доданку нижчого порядку. Теорема 3. Нехай Зауваження. Остання теорема дає змогу при знаходженні границі відношення двох заданих НМ функцій одну чи обидві функції заміняти еквівалентними Н Малими. У цьому допоможе таблиця еквівалентних НМВ:
Друга визначна границя.
Приклад
ЛЕКЦІЯ № 8 з навчальної дисципліни Вища математика Тема. Елементарні функції. Заняття. Функції. Границя функції. Навчальний час – 2 години. Напрямку підготовки – 6.050903 – телекомунікації Для студентів спеціальності – інформаційні мережі зв’язку Навчальна та виховна мета:
1. Студенти повинні знати теоретичні питання з теми «Функції: означення, способи задання, властивості»: основні поняття з даної теми, види елементарних функцій, властивості. 2. Студенти повинні вміти будувати графіки елементарних функцій, описувати їх властивості. 3.Розвиток мислення студентів, залучення до вивчення математики, як необхідної складової фахівця технічного університету
Київ – 20 __ План. 1. Поняття множини. Операції над множинами. Числові множини. 2. Сталі та змінні величини. Поняття функції. Способи задання функції. 3. Основні елементарні функції, їх властивості і графіки. Елементарні функції та їх класифікація. 4. Найпростіші властивості функцій. 5. Функції, задані неявно. Обернені функції. Функції, задані параметрично 6. Границя послідовності та функції. 7. Нескінченно великі та нескінченно малі величини, їх властивості. Порівняння нескінченно малих величин. 8. Основні теореми про границі. 9. Перша та друга визначні границі, наслідки. 10. Неперервність функції, точки розриву та їх класифікація.
ЛІТЕРАТУРА: 1. Барковський В.В., Барковська Н.В. Вища математика для економістів. – К.: ЦУЛ, 2002 – 401 с. 2.Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. – Москва: Наука, – 1988 – 432 с. 3.Валєєв К.Г., Джалладова І.А.Вища математика. НМП для самостійного вивчення дисципліни. – К.: КНЕУ, 2002 – 606с. 4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч 1-2. Москва.: Высшая школа, 1986. 5. Кривуца В.Г., Барковський В.В., Барковська Н.В. Вища математика. Практикум. - К.:ЦУЛ, 2003 – 536 с. 6. Овчинніков П.Ф., Яремчик Ф.П., Михайленко В.М. Вища математика. – К.: Техніка, ч.І 596 с., ч.ІІ 792 с., 2000.
Конспект лекції
Поняття множини. Операції над множинами. Числові множини. Під множиною розуміють сукупність деяких об’єктів, що об’єднуються за певною ознакою чи властивістю. Синоніми: сімейство, клас, набір. Об’єкти, з яких складається множина, називаються її елементами. Множини позначають великими буквами латинського алфавіту: Множину можна задати двома способами: 1) переліком її елементів. Позначення: Приклад. 2) указанням властивості, яку мають всі елементи множини і тільки вони. Така властивість називається характеристичною. Позначення: Приклад. Означення. Множина, яка містить скінченну кількість елементів, називається скінченною. Множина, яка містить нескінченну кількість елементів, називається нескінченною. Означення. Множина, що не містить жодного елемента, називається порожньою. Позначається Приклад. Множина дійсних коренів рівняння Означення. Множину Означення Дві множини називаються рівними, якщо вони містять одні й ті самі елементи. Позначення А=В. За означенням: Означення. Перерізом двох множин
Означення. Об’єднанням двох множин
Означення. Різницею двох множин
|
||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 369; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.65.198 (0.009 с.) |

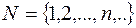


 , де
, де 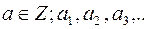 - цифри деякої системи числення
- цифри деякої системи числення :
:
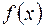 називається парною, якщо для будь – якого х з області визначення
називається парною, якщо для будь – якого х з області визначення  вона задовольняє умову
вона задовольняє умову 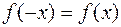

 , непарної – відносно початку координат.
, непарної – відносно початку координат.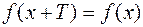 . Число Т називається періодом функції.
. Число Т називається періодом функції. ,
,  Найменший з додатних періодів, якщо він існує, називається основним.
Найменший з додатних періодів, якщо він існує, називається основним. - основний
- основний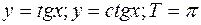 - основний
- основний - (с – стала) Т – довільне ненульове число, не існує основного періоду.
- (с – стала) Т – довільне ненульове число, не існує основного періоду.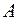 називається обмеженою на цій множині, якщо існує таке число
називається обмеженою на цій множині, якщо існує таке число  , що для всіх
, що для всіх 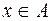 виконується нерівність
виконується нерівність 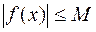 .
.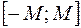 , тому її графік лежить між прямими
, тому її графік лежить між прямими 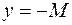 та
та 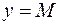 .
. обмежені на R.
обмежені на R. , що виконується нерівність
, що виконується нерівність 
 обмежена знизу прямою
обмежена знизу прямою  (віссю Ох) і необмежена зверху. Функція
(віссю Ох) і необмежена зверху. Функція  необмежена.
необмежена.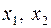 з області визначення функції
з області визначення функції  з нерівності
з нерівності 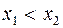 випливає, що
випливає, що , то функція називається зростаючою.
, то функція називається зростаючою. , то функція називається неспадною.
, то функція називається неспадною.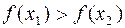 , то функція називається спадною.
, то функція називається спадною. , то функція називається незростаючою.
, то функція називається незростаючою.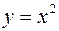 не монотонна на R, але має два проміжки монотонності: на
не монотонна на R, але має два проміжки монотонності: на  вона спадає, на
вона спадає, на 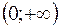 зростає.
зростає. , то кажуть, що функція задана явно (є явною).
, то кажуть, що функція задана явно (є явною). , не розв’язаним відносно змінної
, не розв’язаним відносно змінної 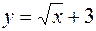 - явна функція;
- явна функція; - неявна функція
- неявна функція у відповідність єдиний елемент
у відповідність єдиний елемент  з області визначення функції
з області визначення функції  , називається оберненою для функції f.
, називається оберненою для функції f. . За означенням
. За означенням 
 є оберненою до функції
є оберненою до функції  , якщо
, якщо є множина значень функції
є множина значень функції  .
. є областю визначення функції
є областю визначення функції  .
. відповідає єдине значення
відповідає єдине значення  .
. є оберненою до іншої.
є оберненою до іншої. не має оберненої; на
не має оберненої; на 
 має обернену
має обернену
 має обернену
має обернену 
 не має оберненої.
не має оберненої. і
і  нескінченно малі при
нескінченно малі при  , називаються еквівалентними НМ, якщо
, називаються еквівалентними НМ, якщо 



 ,
,  при
при  . Якщо існує
. Якщо існує 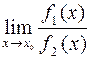 , то існує і
, то існує і  і ці границі рівні між собою.
і ці границі рівні між собою.





 ,
, 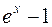

 ,
, 

 ,
, 
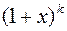 -1
-1  ,
, 
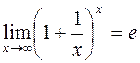 ;
; 

 , а їх елементи – малими:
, а їх елементи – малими:  . Запис
. Запис  означає, що елемент
означає, що елемент  належить множині
належить множині  означає, що елемент
означає, що елемент 

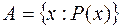

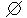 .
. . Множина людей на Сонці.
. Множина людей на Сонці.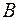 називають підмножиною множини
називають підмножиною множини  або
або 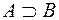 (
( й
й 
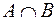 , яка складається з елементів, кожен з яких належить множинам
, яка складається з елементів, кожен з яких належить множинам 
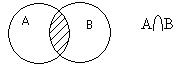
 , яка складається з елементів, кожен з яких належить хоча б одній з множин
, яка складається з елементів, кожен з яких належить хоча б одній з множин 

 , яка складається з елементів, кожен з яких належить множині
, яка складається з елементів, кожен з яких належить множині 




