
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 1. Элементы математической логики. Математические доказательстваСодержание книги
Поиск на нашем сайте
Учебное пособие
Киров Рецензенты: А.В. Черанева, кандидат физико-математических наук, доцент кафедры ПМиИ ВятГУ; В.В. Утемов, преподаватель математики и информатики ГОУ СПО «Кировский областной колледж культуры».
Чернядьева Е.Н. Задачник по математике: учебное пособие. – Киров: Изд-во КИПК и ПРО, 2010. – 60 с.
Настоящее пособие является сборником задач по математике для студентов ГОУ СПО «Кировский областной колледж культуры». Расположение задач соответствует структуре учебной программы.
© Е.Н. Чернядьева, 2010 © КИПК и ПРО Оглавление Оглавление. 3
Введение. 4
Раздел 1. Элементы математической логики. Математические доказательства 5 Тема 1.1. Софизмы.. 5 Тема 1.2. Высказывания и операции над ними.. 15 Тема 1.3. Неопределенные высказывания. Кванторы.. 25 Тема 1.4. Логические задачи.. 29 Раздел 2. Математические методы в целенаправленной деятельности. 35 Тема 2.1. Понятие вероятности случайных событий. Случайные величины 35 Тема 2.2. Характеристики законов распределения. 42 Тема 2.3. Основы математической статистики.. 46
Ответы, указания. 54 Тема 1.1.. 54 Тема 1.2.. 55 Тема 1.3.. 56 Тема 1.4.. 56 Тема 2.1.. 57 Тема 2.2.. 58 Тема 2.3.. 59
Список литературы.. 60
Введение
«Задачник по математике: учебное пособие» предназначен для студентов специальности 071302 «Социально-культурная деятельность и народное художественное творчество» ГОУ СПО «Кировский областной колледж культуры» и составлен с целью показать практическое применения полученных знаний и использование математики в гуманитарных исследованиях, учить студентов рассуждать, размышлять и делать верные выводы. Данное пособие структурировано в соответствии с требованиями к минимуму содержания и уровню подготовки выпускников по данной специальности дисциплины «Математика и информатика», в пределах каждого раздела в соответствии с тематическим планом. В каждой теме освещены основные аспекты теоретического материала: даны понятия, определения, формулы, примеры на их понимание, что позволяет студентам овладеть необходимыми базовыми знаниями. Основу пособия составляют задачипро жизненные ситуации студентов ГОУ СПО «Кировский областной колледж культуры», что вызывает интерес к их решению у самих студентов. Представленные задачи имеют разный уровень сложности и даны в достаточно большом объеме. Некоторые задачи целесообразно решать устно. Это относится к логическим софизмам и тренировочным задачам на понимание определений. Некоторые задачи не является стандартными, для их решения требуются не только базовые знания и умения, но и умение мыслить, рассуждать, доказывать. Для удобства читателя в учебном пособии принята сквозная нумерация. Задачи распределены по разделам, каждый из которых разбит на темы. Если решение каких-то задач вызовут сомнения в их правильности, то на помощь придет раздел «Ответы и указания». Раздел 1. Элементы математической логики. Математические доказательства Тема 1.1. Софизмы «Правильно понятая ошибка– это путь к открытию». И. П. Павлов. Софизм – (от греческого sophisma – мастерство, умение, хитрая выдумка, уловка) умозаключение или рассуждение, обосновывающее какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, которое при поверхностном рассмотрении кажется правильным. Софизм основан на преднамеренном, сознательном нарушении правил логики. Каким бы ни был софизм, он всегда содержит одну или несколько замаскированных ошибок. Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки. Очень часто понимание ошибок в софизме ведет к пониманию математики в целом, помогает развивать логику и навыки правильного мышления. Если нашел ошибку в софизме, значит, ты ее осознал, а осознание ошибки предупреждает от ее повторения в дальнейших математических рассуждениях. Софизмы не приносят пользы, если их не понимать. Задачи Найдите ошибку в софизмах: 1. Нам чужого не надо. То, что нам не надо, мы продаем. Получатся, мы продаем чужое. 2. То, что мы не теряли, мы имеем. Мы не теряли рогов. Значит, мы их имеем. 3. Лекарство, принимаемое больным, есть добро. Чем больше делать добра, тем лучше. Значит, лекарств нужно принимать как можно больше. 4. Все существительные меняют падежные окончания. Слово «синий» меняет падежные окончания. Следовательно, слово «синий» – существительное. 5. Софизм Зенона. Быстроногий Ахиллес никогда не настигнет черепаху. Пока Ахиллес добежит до черепахи, она продвинется немного вперед. Он быстро преодолеет это расстояние, но черепаха уйдет еще чуточку вперед. И так до бесконечности. Всякий раз, когда Ахиллес будет достигать места, где была перед этим черепаха, она будет оказываться хотя бы немного, но впереди. 6. Вор не желает приобрести ничего дурного. Приобретение хорошего есть дело хорошее. Следовательно, вор желает хорошего. 7. Сидящий встал; кто встал, тот стоит; следовательно, сидящий стоит. 8. Для того чтобы видеть, вовсе необязательно иметь глаза: ведь без правого глаза мы видим, без левого тоже видим; кроме правого и левого, других глаз у нас нет; поэтому ясно, что глаза не являются необходимыми для зрения. 9. Одна песчинка не есть куча песка. Если n песчинок не есть куча песка, то и n+ 1 песчинка – тоже не куча. Следовательно, никакое число песчинок не образует кучу песка. 10. Движущийся предмет должен дойти до половины своего пути прежде, чем он достигнет его конца. Затем он должен пройти половину оставшейся половины, затем половину этой четвертой части и т.д. до бесконечности. Предмет будет постоянно приближаться к конечной точке, но так никогда ее не достигнет. 11. Вполне возможно, что лгун сознается в том, что он лгун. В таком случае он скажет правду. Но тот, который говорит правду, не есть лгун. Следовательно, возможно, что лгун не есть лгун. Какая ошибка? 12. Пусть имеется стакан, наполненный водой до половины. Тогда можно сказать, что стакан, наполовину полный равен стакану, наполовину пустому. Увеличивая обе части равенства вдвое, получим, что стакан полный равен стакану пустому. 13. – Знаете ли вы, о чем я хочу вас спросить? – Нет. – Знаете ли вы, что врать нехорошо? – Знаю. – Об этом я и хотел тебя спросить, а ты ответил, что не знаешь, выходит, ты не знаешь то, что знаешь. 14. В приведенных ниже стихах, взятых из одного английского журнала, выходившего в прошлом веке, рассказывается о хитром хозяине гостиницы, сумевшем разместить в девяти номерах десять гостей так, что каждому из них досталось по отдельной комнате. Их было десять чудаков, – Пусти, хозяин, ночевать, Хозяин тем гостям был рад, – Восьми гостям я предложу Лишь он сказал, и сразу крик, От гнева красны лица: Никто из всех десятерых Не хочет потесниться. Как охладить страстей тех пыл, Умерить те волненья? Но старый плут хозяин был И разрешил сомненья. Двух первых путников пока, Спал третий в «Б», четвертый в «В», Потом, вернувшись снова в «А», Хоть много лет с тех пор прошло, Иль арифметика стара, Иль чудо перед нами, Понять, что, как и почем Уж Вы постарайтесь сами 15. – Скажи, – обращается софист к молодому любителю споров,– может одна и та же вещь иметь какое-то свойство и не иметь его? – Очевидно, нет. – Посмотрим. Мед сладкий? – Да. – И желтый тоже? – Да, мед сладкий и желтый. Но что из этого? – Значит, мед сладкий и желтый одновременно. Но желтый – это сладкий или нет? – Конечно, нет. Желтый – это желтый, а не сладкий. – Значит, желтый – это не сладкий? – Конечно. – О меде ты сказал, что он сладкий и желтый, а потом согласился, что желтый не значит сладкий, и потому как бы сказал, что мед является и сладким, и несладким одновременно. А ведь вначале ты твердо говорил, что ни одна вещь не может и обладать, и не обладать каким-то свойством. 16. Софизм Эватла. Эватл брал уроки софистики у софиста Протагора под тем условием, что гонорар он уплатит только в том случае, если выиграет первый процесс. Ученик после обучения не взял на себя ведения какого-либо процесса и потому считал себя вправе не платить гонорара. Учитель грозил подать жалобу в суд, говоря ему следующее: «Судьи или присудят тебя к уплате гонорара или не присудят. В обоих случаях ты должен будешь уплатить. В первом случае в силу приговора судьи, во втором случае в силу нашего договора». На это Эватл отвечал: «Ни в том, ни в другом случае я не заплачу. Если меня присудят к уплате, то я, проиграв первый процесс, не заплачу в силу нашего договора, если же меня не присудят к уплате гонорара, то я не заплачу в силу приговора суда». 17. Некто взялся доказать, что дважды три равно четырем, а не шести. Для этого он попросил одного из присутствующих из плотной бумаги отрезок. – Разрезав этот отрезок пополам, – сказал он, – будем иметь один раз 2. Проделав то же самое над одной из половинок, будем иметь второй раз 2, проделав ту же операцию над другой из половинок, получим третий раз 2. Беря три раза по два, мы получили 4, а не 6. 18. Некто утверждал, что 45-45=45. Рассуждал он так: «Записываем вычитаемое в виде суммы последовательных натуральных чисел от 1 до 9, а уменьшаемое в виде суммы тех же чисел, но взятых в обратном порядке (от 1 до 9): 9+8+7+6+5+4+3+2+1 1+2+3+4+5+6+7+8+9 8+6+4+1+9+7+5+3+2 Будем последовательно вычитать числа второй строки из чисел первой. Например, так как 9 из 1 вычесть нельзя, то занимаем единицу из двух, имеем 11-9=2 и т. д. Теперь нетрудно установить, 8+6+4+1+9+7+5+3+2=45. Итак, 45-45=45». 19. Докажем, что 5 – четное и нечетное число одновременно. 5 есть 2 + 3 («два и три»). Два – число четное, три – нечетное, выходит, что пять – число и четное и нечетное. 20. Ниже показано, что один рубль не равен ста копейкам. Известно, что любые два неравенства можно перемножать почленно, не нарушая при этом равенства, т.е.если a=b, c=d, то ac=bd. Применим это положение к двум очевидным равенствам 1 р.=100 коп, (1) 10 р.=10 · 100 коп.(2) перемножая эти равенства почленно, получим 10 р.=100000 коп. и, наконец, разделив последнее равенство на 10 получим, что 1 р.=10 000 коп. таким образом, один рубль не равен ста копейкам. 21. Деятельный бездельник Боб Бабкинс нажил неправедным трудом двух лошадей и решил продать их за 25$. На ярмарке он встретил ковбоя Джо и ковбоя Билла и продал им каждого коня за 12,5$. Но тут вмешался шериф Мортон, решивший, что цена за пару старых кляч слишком высока. Припугнув Боба, он велел вернуть каждому ковбою по 2,5$. Пока Боб Бабкинс снова искал Джо и Билла, он увидел, что продают его любимые леденцы, не удержался и потратил на них 3$. После этого он нашел ковбоев и отдал им оставшиеся деньги – каждому по доллару. Вернувшись домой Боб задумался. Получилось, что раз он вернул по одному доллару, то ковбои заплатили за каждую лошадь по 11,5$. Значит, оба коня вместе стоили 23$. И 3$ Боб Бабкинс потратил на леденцы, следовательно, всего получается 26$. Но ведь было всего 25$. 22. – Скажи, – обращается софист к молодому любителю споров,– может одна и та же вещь иметь какое-то свойство и не иметь его? – Очевидно, нет. – Посмотрим. Мед сладкий? – Да. – И желтый тоже? – Да, мед сладкий и желтый. Но что из этого? – Значит, мед сладкий и желтый одновременно. Но желтый – это сладкий или нет? – Конечно, нет. Желтый – это желтый, а не сладкий. – Значит, желтый - это не сладкий? – Конечно. – О меде ты сказал, что он сладкий и желтый, а потом согласился, что желтый не значит сладкий, и потому как бы сказал, что мед является и сладким, и несладким одновременно. А ведь вначале ты твердо говорил, что ни одна вещь не может и обладать, и не обладать каким-то свойством. 23. Докажем, что дважды два – пять! Возьмем в качестве исходного соотношения следующее очевидное равенство: 4:4= 5:5. После вынесения за скобки общего множителя из каждой части равенства будем иметь: 4·(1:1)=5·(1:1) или (2·2)(1:1)=5·(1:1) Наконец, зная, что 1:1=1, мы из соотношения 4(1:1)=5(1:1)устанавливаем: 2·2=5. 24. Еще один софизм: дважды два пять! 16-36=25-45 16-36+81/4=25-45+81/4 42-2·4·9/2+(9/2)2=52-2·5·9/2+(9/2)2 (4-9/2)2= (5-9/2)2 (4-9/2)= (5-9/2) 4=5 2·2=5 25. И еще один софизм: дважды два пять! Обозначим 4 =а, 5 =b, (a+b) /2 =d. Имеем: a+b= 2 d, a= 2 d-b, 2 d-a=b. Перемножим два последних равенства по частям. Получим: 2 da-a · a= 2 db-b · b. Умножим обе части получившегося равенства на -1 и прибавим к результатам d · d. Будем иметь: a2- 2 da+d2=b2 -2 bd+d2, или (a-d)(a-d)=(b-d)(b-d), откуда a-d=b-d и a=b, т.е. 2·2=5 26. Докажем, что отрицательное число больше положительного.
27. Докажем, что единица равна нулю. Возьмем уравнение: x-a=0 Разделив обе его части на х-а, получим: х-а/х-а= 0 /х-а Откуда сразу же получаем требуемое равенство: 1= 0. 28. Ниже доказано, что любое число а равно меньшему числу b. Начнем с равенства а = b + c. Умножив обе его части на (a - b), получим а² - аb = аb + аc - b² - bс. Перенесем ас в левую часть: а² - аb - аc = аb - b² - bс и разложим на множители: а(а - b - c) = b(а - b -c). Разделив обе части равенства на (а - b - c), найдем а = b, что и требовалось доказать. 29. Ниже доказано, что число, равное другому числу, одновременно и больше, и меньше его. Возьмем два положительных равных числа a и b и напишем для них следующие неравенства: a > - b b > - b. Перемножив оба этих неравенства почленно, получим неравенство a·b>b·b, разделим его на b (это законно, т.к. b>0), получим a > b. Записав же два других столь же бесспорных неравенства: b > - a a > - a Перемножив оба этих неравенства почленно, что b·a > a·a, а разделив на a>0, получим b·a > a·a, разделим на а>0, придем к b > a. Итак, число a, равное числу b, одновременно и больше, и меньше его. 30. Спичка вдвое длиннее телеграфного столба. Пусть, а дм - длина спички и b дм - длина столба. Разность между b и a обозначим через c. Имеем b - a = c, b = a + c. Перемножаем два эти равенства по частям, находим: b2 - ab = ca + c2. Вычтем из обеих частей bc. Получим: b2- ab - bc = ca + c2 - bc, или b(b - a - c) = - c(b - a - c), откуда b = - c, но c = b - a, поэтому b = a - b, или a = 2 b. 31. Если вырезать из бумаги в клетку треугольник и разрезать его так, как показано на рис. 1, а затем сложить вырезанные части так, как показано на рис. 2, то получится, что площадь первого треугольника 60 клеток, а второго на 2 меньше.
Рис. 1 Рис. 2
Задачи 32. Определите, является предложение высказыванием или нет. Ответ обоснуйте. 1. Москва – столица США. 2. Треугольник АВС подобен треугольнику A’B’C’. 3. Студент группы 2ТП. 4. 2+3-1. 5. Кислород – газ. 6. Каша – вкусное блюдо. 7. Наступили каникулы! 8. х= 2. 9. Математика – интересный предмет. 10. Железо тяжелее свинца. 11. Да здравствуют музы! 12. Треугольник называется равносторонним, если все его стороны равны. 13. Ты получаешь стипендию? 14. Сегодня плохая погода. 15. Дует ветер. 16. Ты поедешь завтра домой? 17. Сходи завтра в библиотеку. 18. 2-3 = 5. 19. В романе А.С. Пушкина «Евгений Онегин» 136245 букв. 20. Река Ангара впадает в озеро Байкал. 21. Через некоторое время пойдет снег. 22. Сегодня при входе в колледж давали апельсины. 23. Самый вкусный в мире напиток – квас. 24. Я хорошо танцую. 25. В нашей группе учатся только юноши. 26. Через час вам подарят букет роз. 27. Евгений Плющенко – олимпийский чемпион по фигурному катанию. 28. Завтра в городе пойдет снег. 29. Гагарин – первый человек, полетевший в космос. 30. Лев Лещенко – мер Москвы. 31. Луна – спутник планеты Земля. 32. В русском алфавите 35 букв. 33. Стоимость компьютера в 20 000 рублей – это дешево. 34. 2 х- 1=0. 35. Ты хочешь быть отличником? 33. Придумайте свое простое высказывания. 34. Определите, сложным или простым является высказывание. Если вы считаете, что высказывание сложное, то назовите логических связки, с помощью которых оно образовано. а) Вася любит мороженное «Мальвина» и «Спортивное». б) Я не болен, вчера немного простудился. в) Лилии, розы, маргаритки – вот любимые цветы Наташи. г) Может, после уроков я пойду гулять, а может, поеду на экскурсию. д) Когда вы сдадите все вступительные экзамены на «отлично», можете не сомневаться, что вы поступите. е) Коля любит все шоколадные конфеты, у которых начинка мармеладная. ж) Я сделаю сегодня домашнее задание, если возьму учебник. з) Мама заказала мне купить в магазине либо фломастеры, либо маркеры. и) Мне разрешают гулять родители, если и только если я делаю все уроки. к) Костя не занимается волейболом и баскетболом. 35. Прочтите высказывания, составленные с помощью логических связок из ниже приведенных простых высказываний: А – «Я – студент Кировского областного колледжа культуры», В – «За учебу на « 4 » и « 5 » студенты получают стипендию», С – «Быть хореографом – моя мечта с детства». а) C→A. б) в) г) д) B ~ C. е) ж) з) и) к) 36. В следующих примерах запишите пословицу в виде логического следствия (импликации), используя связку «если..., то...». Выделите высказывания А и В. Запишите в краткой и словесной формах прямое, обратное, противоположное и противоположное обратному утверждения. Определите их значения истинности. 1) Горя бояться – счастья не видать. 2) Чем дальше в лес, тем больше дров. 3) Волков бояться – в лес не ходить. 4) Не было бы счастья, да несчастье помогло. 5) Нет худа без добра. Приведите свои примеры. 37. Составьте сложные высказывания, используя логические связки и следующие простые высказывания: А – «У меня есть права на управление автомобилем», В – «Мой автомобиль красного цвета», С – «Мне 18 лет». 38. Придумайте свое сложное высказывание. 39. Составьте отрицания высказываний. а) Некоторые студенты получают стипендию. б) Киров – культурная столица России. в) Белые медведи живут в Арктике. г) 2·2=4. д) В английском алфавите 40 букв. е) В году 12 месяцев. ж) Все металлы проводят электричество. з) Каждый из студентов первого курса получает стипендию. и) Петров И.И. – студент МГУ. к) Япония – капиталистическая страна. 40. Установите, какие из следующих высказываний являются отрицанием друг друга и какие – нет (объясните почему): а) 2<0, 0>2. б) 6>9, 6≤9. в) «Натуральное число с четно», «Натуральное число с нечетно». г) «Функция f четная», «Функция f нечетная». д) «Все простые числа четны», «Все простые числа нечетны». е) «Человеку известны все виды животных, обитающих на Земле», «На Земле есть вид животных, неизвестный человеку». ж) «Вы студенты группы 2ХФ», «Вы студенты группы 2СБ». з) «Если на улице идет дождь, то крыши домов мокрые», «Если на улице не идет дождь, то крыши домов сухие». и) «Лица, занимающиеся мошенничеством, привлекаются к уголовной ответственности». «Лица, не занимающиеся мошенничеством, не привлекаются к уголовной ответственности». к) «Если воздушный шарик задеть острым предметом, то он лопнет». «Если воздушный шарик не задеть острым предметом, то он не лопнет». 41. Сформулируйте позитивные отрицания (без частицы НЕ): а) Некоторые студенты получают стипендию. б) Киров – культурная столица России. в) Белые медведи живут в Африке. г) 2·2=4. д) В английском алфавите 40 букв. е) В году 12 месяцев. ж) Все металлы проводят электричество. з) Каждый из студентов первого курса получает стипендию. и) Петров И.И. – студент МГУ. к) Япония – капиталистическая страна. 42. Сформулируйте отрицания следующих высказываний, постарайтесь придумать позитивные и негативные отрицания: а) Волга впадает в Каспийской море. б) Число 28 не делится на число 7. в) 6>3. г) 4≤5. д) Все простые числа нечетны. е) Ртуть – металл. ж) Некоторые капиталистические страны – члены НАТО. з) Некоторые студентов ВятГГУ – бывшие военнослужащие. и) Коренные жители Конго – негры. к) 1,5 – десятичная дробь. л) Если число оканчивается нулем или цифрой пять, то оно делится на 5. м) Студент Орлов – отличник. н) -8 – отрицательное число. о) Неверно, что все млекопитающие живут на суше. п) Неверно, что некоторые собаки летают. р) Неверно, что 43. Составьте алгоритм получения позитивного сложного высказывания. 44. Определите истинность следующих сложных высказываний, составленных из простых высказываний А, В, С, если А – истина, В – ложь, С – ложь. а) б) в) B ~ C. г) д) е) ж) з) и) к) л) м) н) о) п) ( р) 45. Докажите верность следующих законов логики: а) б) в) 46. Проверьте, верны ли следующие равенства: а) б) в) г) д) е)
Задачи 47. Выберите из ниже предложенных предложений предикаты: а) В некотором городе есть кремль. б) Х – четное число, где Х – множество натуральных чисел от 1 до 10. в) 2+ Y = 4. г) Все дети любят конфеты. д) Света сестра Х, где Х – студент группы 2 курса. е) A брат B. ж) Х = 4, ХÎ N. з) В – целое число. 48. Какие кванторы задействованы в построении следующих предложений: а) Не все животные живут в лесу. б) Некоторые студенты живут в общежитии. в) Не каждый прохожий может ответить на вопрос «который час». г) Большинство мужчин являются кормильцами в семье. д) Какие-то студенты получают повышенную стипендию. е) Хоть кто из взрослых людей сможет проехать на самокате. ж) Ни одна из компаний не поддержала торги на бирже. з) Две трети группы ходили в поход. и) Все люди работают. к) Многие люди имеют высшее образование. л) Никто из группы 2Б не пришел вчера на собрание. м) Любое натуральное число четно. н) Есть в нашем колледже такие студенты, которые отлично учатся. о) Хотя бы у одного студента группы специализации «Фотовидеотворчество» есть фотоаппарат. п) Кто-то вчера из студентов проспал уроки. 49. Придумайте по 5 высказываний с квантором существования и с квантором всеобщности, выражая их различными словами. 50. Из ниже предложенных предикатов получите высказывания несколькими способами: а) А – «Х – нечестное число», Х Î{1,2,3,4,5}. б) В – «В городе Х ездят трамваи», Х – множество городов России. в) С – «По реке Х плавают теплоходы», где Х – реки Кировской области. г) D – «Студент Х учится на 2 курсе», где Х – студенты Кировского областного колледж культуры. д) Е – «В кабинете Х есть компьютер», где Х - кабинеты Кировского областного колледж культуры. е) F – «Х – положительное число», где Х Î{-2, -1, 1, 2}. ж) J – «Студент Х живет в общежитии», где Х – студенты 2-го курса Кировского областного колледж культуры. г) К – «Студент Х живет в общежитии», где Х – множество студентов Кировского областного колледж культуры. д) L – «Студент Х учится в одной группе со студенткой Y», где Х –множество юношей Кировского областного колледж культуры и Y – множество девушек Кировского областного колледж культуры. 51. Постройте отрицания высказываний с кванторами, которые у вас получились в задании 2. 52. Постройте отрицания ниже приведенных высказываний: а) Каждый студент 2-го курса получает стипендию. б) Все знаменитые женщины – математики. в) Есть такие слова в русском языке, которые пишутся и читаются по-разному. г) Хотя бы один студент группы 2ТП выступал на сцене. д) Все книги в библиотеке отмечены штампами на 3 странице. е) Любой символ в условии задачи важен для ее решения.
Тема 1.4. Логические задачи Логика, которая одна может дать достоверность, есть орудие доказательства. А. Пуанкаре Задачи 53. Запишите высказывания, равносильные данным предложениям с помощью букв и операций над высказываниями: а) Сегодня шел дождь и снег. б) Погода была солнечной, и температура повысилась до 20 градусов. в) Я езжу домой на автобусе или троллейбусе. г) Если прозвенел звонок, то урок окончен. д) Треугольник называется равнобедренным тогда и только тогда, когда две его стороны равны. е) Если не решать задачи, то не напишешь контрольную работу по математике на 5. ж) Неверно, что ковбой Билл встретил живого динозавра или знакомого инопланетянина. з) Неверно, что папа купил в магазине “Инструмент” набор кастрюль или живого слона. и) Неверно, что кошки не пьют молоко и не едят рыбу. к) Киров – столица России тогда и только тогда, когда Анастасия Волочкова – не балерина. л) Два треугольника равны тогда и только тогда, когда все их стороны или углы равны между собой. м) Если алгоритм записан на языке, а язык понятен исполнителю, то алгоритм превращается в программу. н) Если у регулировщика руки вытянуты в стороны или опущены, то со стороны спины движение всем запрещено. о) Если внимательно слушать преподавателя на занятии и выполнять домашнее задание, то знания и оценка по предмету будет хорошие. п) Если у рассматриваемого транспортного средства ровно 2 колеса и есть двигатель, то рассматриваемое транспортное средство – мопед или мотоцикл. 54. Определите значения истинности высказываний А, В, С, D, Е если: а) б) в) г) д) 55. Определите значения истинности высказываний А, В, С, D, Е, F, J, K если: а) А ® (2 × 2 = 5) – истинное высказывание. б) В ® (2 × 2 = 5) – ложное высказывание. в) С ~ (2 × 2 = 4) – истинное высказывание. г) D ~ (2 × 2 = 5) – ложное высказывание. д) (2 × 2 = 4) ® E – ложное высказывание. е) (2 × 2 = 4) ® D – истинное высказывание. ж) (2 × 2 = 5) ~ F – ложное высказывание. з) (2 × 2 = 5) ~ J – истинное высказывание. и) (2 × 2 = 5) ® K – истинное высказывание. 56. Определите значения истинности высказывания С: а) B ~ C – истинное высказывание. б) A ® В – ложное высказывание, С ® В – истинное высказывание. в)
г)
д)
е) (А ~ В) 57. Определите значения истинности высказывания D: а)
б) С ~ В – истинное высказывание,
в)
С ® D – истинное высказывание. г)
С ~ D – истинное высказывание. д)
е) С ~ В – ложное высказывание,
58. Определите значения истинности высказываний А и В: а) А ~ В – ложное высказывание, A ® В – истинное высказывание. б) А ~ A ® В – истинное высказывание. в) А ~ В – истинное высказывание. г) А ~ В – истинное высказывание. д)
A ® В – истинное высказывание. е)
А ~ В – истинное высказывание. ж) A ® В – истинное высказывание, А ~ В – истинное высказывание. з) A ® В – истинное высказывание, А ~ 59. Определите значение истинности сложного высказывания: а) А ~ В – истинное высказывание. Найти истинность высказывания (
|
||||
|
Последнее изменение этой страницы: 2017-02-16; просмотров: 316; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.82.208 (0.012 с.) |




 .
. .
. .
. .
.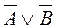 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.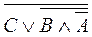 .
. ~
~  .
.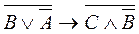 ) ~А.
) ~А. ~
~  .
. .
. .
. .
.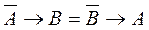 .
.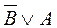 =
=  .
. .
.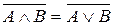 .
. ~ В=
~ В=  .
. – истинное высказывание.
– истинное высказывание.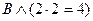 – ложное высказывание.
– ложное высказывание. – истинное высказывание.
– истинное высказывание. – ложное высказывание.
– ложное высказывание.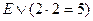 – ложное высказывание.
– ложное высказывание. – истинное высказывание,
– истинное высказывание, – ложное высказывание,
– ложное высказывание, – истинное высказывание.
– истинное высказывание. - ложное высказывание,
- ложное высказывание, – ложное высказывание.
– ложное высказывание.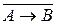 – истинное высказывание,
– истинное высказывание, ~C – истинное высказывание.
~C – истинное высказывание. – истинное высказывание,
– истинное высказывание, – истинное высказывание.
– истинное высказывание.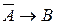 – ложное высказывание,
– ложное высказывание, – истинное высказывание,
– истинное высказывание,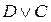 – истинное высказывание.
– истинное высказывание. – истинное высказывание.
– истинное высказывание. – истинное высказывание,
– истинное высказывание, – истинное высказывание,
– истинное высказывание,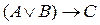 – истинное высказывание,
– истинное высказывание,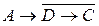 – истинное высказывание.
– истинное высказывание. – истинное высказывание.
– истинное высказывание.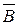 – истинное высказывание,
– истинное высказывание, – истинное высказывание,
– истинное высказывание, – истинное высказывание,
– истинное высказывание,



