
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка основного закона динамики вращательного движения на основе маятника ОбербекаСодержание книги
Поиск на нашем сайте
Выполнил студент группы:
Проверил преподаватель:
Приложение 2 Приближенные значения некоторых фундаментальных физических постоянных
Приложение 3 Значения работы выхода электронов из некоторых материалов
Приложение 4 Обработка погрешностей 1. Погрешности прямых измерений В основе теории определения случайных погрешностей прямых измерений1 лежат положения, разработанные Гауссом. 1) Погрешности равной абсолютной величины и противоположных значений равновероятны 2) Чем больше абсолютная величина погрешности, тем она менее вероятна. Пусть n – число произведенных измерений некоторой величины А. При этом получен некоторый ряд значений этой величины А1, А2, А3, …Аn. Найдем среднее арифметическое значение величины А:
Найдем абсолютную погрешность каждого измерения, которая определяется как отклонение каждой измеряемой величины от истинного значения. Поскольку истинное значение неизвестно, то за величину, близкую к истинной, принимается среднее арифметическое значение (1):
При достаточно большом числе измерений границы погрешностей симметричны. Их можно оценить с помощью среднего квадратического отклонения результата измерения:
Или стандартного отклонения (оценка среднеквадратического отклонения случайной величины относительно её математического ожидания):
При этом предполагается, что измерения производятся приборами, собственная погрешность которых значительно меньше погрешностей отдельных измерений DАi. Следует отметить, что в измерительных приборах, если нет указаний на класс точности, за абсолютную погрешность можно принимать половину цены деления шкалы. Числовое значение результата измерений должно оканчиваться цифрой того же порядка, что и значение погрешности S(A).
2. Погрешности косвенных измерений Зачастую приходится определять физические величины из так называемых косвенных измерений, т.е., подстановкой непосредственно измеряемых величины в расчетные формулы. Рассмотрим основные положения, позволяющие определить погрешность косвенных измерений. 1) Абсолютная погрешность алгебраической суммы равна сумме абсолютных погрешностей измеряемых величин:
2) Абсолютная погрешность алгебраической разности величин также равна сумме абсолютных погрешностей измеряемых величин, поскольку наличие нескольких погрешностей только ухудшает общую погрешность:
3) Относительная погрешность произведения или частного равна сумме относительных погрешностей величин, входящих в формулу с коэффициентами, равными показателям степени этих величин. При этом, в случае отрицательной степени погрешность все равно берется с положительным знаком, чтобы учесть наихудшую погрешность. 4) Если расчетная формула измеряемой величины включает произведение нескольких сомножителей, то рациональнее вначале определить относительную погрешность, а затем – абсолютную.
5) Исходя из математического определения дифференциала натурального логарифма, можно найти относительную погрешность путем логарифмирования расчетной формулы с последующими дифференцированием.
Пример расчета погрешности косвенных измерений Пусть расчетная формула для величины x имеет вид:
Логарифмируем и получим:
Берем полный дифференциал выражения:
Принимая во внимание, что Окончательно получаем
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 332; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.62.5 (0.009 с.) |

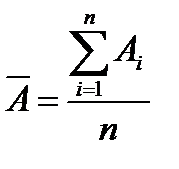 (1)
(1) (2)
(2)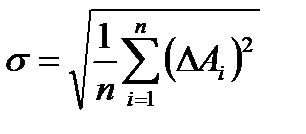
 (3)
(3) (4)
(4) (5)
(5) (6)
(6) (7)
(7) (8)
(8)
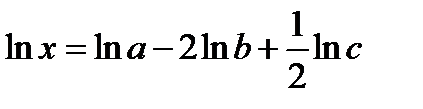


 ,
,  и т.д. есть относительные погрешности каждой из величин, знак при
и т.д. есть относительные погрешности каждой из величин, знак при  изменяем на «плюс» (смотрите пункт 3)).
изменяем на «плюс» (смотрите пункт 3)).



