
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение свободных колебаний в электрическом контуре
ЦЕЛЬ РАБОТЫ
2. Исследовать влияние величин электроемкости и индуктивности на период колебаний в контуре с малым сопротивлением. 3. Установить характер зависимости логарифмического декремента затухания колебаний от сопротивления контура.
КРАТКАЯ ТЕОРИЯ Исследуемый контур состоит из конденсатора электроемкостью С, катушки с индуктивностью L и резистора, имеющего сопротивление R. Схема соединения элементов электрической цепи приведена на рисунке 1.
Простой контур, который здесь рассматривается, является электрической цепью со сосредоточенными параметрами. Это означает, что электроемкость С сосредоточена в одном месте (конденсаторе), а индуктивность L и сопротивление R- в других местах контура (в катушке и в резисторе). Электрическими колебаниями в таком случае выступают повторяющиеся изменения электрических величин, характеризующих процессы в элементах контура. В конденсаторе, например, изменяются со временем следующие величины: заряд q и напряжение между обкладками Электрические колебания (процессы) происходят во всех элементах цепи согласованно. А именно так, что мгновенные значения силы тока i одни и те же в любом месте контура. Подобное имеет место в цепи постоянного (стационарного) тока. Поэтому электрические процессы в колебательном контуре называются квазистационарными «квази»- приставка, означающая «якобы, как будто». Квазистационарные процессы также подчиняются закону Ома, что и постоянный ток. Для математического описания электрических процессов в контуре применим 2 закон Кирхгофа: «Сумма падений напряжения в контуре равна сумме действующих в нем ЭДС». В колебательном контуре имеются два падения напряжения: на конденсаторе
Сила тока по определению связана с зарядом конденсатора соотношением:
Подставив выражения для тока i и напряжения
После введения обозначений оно принимает вид:
В качестве решения этого дифференциального уравнения второго порядка рассмотрим вначале функцию:
(3) в которой
где равенство нулю возможно для всех значений t тогда, когда коэффициенты при cos-е и sin-е равны нулю, поэтому имеем:
Итак, функция Амплитуда заряда на конденсаторе
(5)
Наконец, постоянные величины
Теперь обратим внимание на такие особенности колебательного процесса с затуханием, которые на рисунке заметить нельзя. Для этого найдем уравнение колебаний тока в контуре, приняв уравнение колебаний заряда в виде
Записав слагаемое диаграммы, получим уравнение колебаний тока в виде:
где (см. соотношение 4), а есть сдвиг фаз между колебаниями заряда и тока.
Полученный результат приводит к следующим заключениям: 1. Амплитуда тока в начальный момент времени 2. В контурах с малым сопротивлением R и достаточно большой частотой 3. Затухание влияет на частоту Полученная ранее формула (4) позволяет рассчитать относительную разницу величин
(7)
При отношении В результате при слабом затухании уравнения колебаний заряда и тока можно приближенно записать так:
(8)
Отметим, что период колебаний Точное же значение периода затухающих колебаний (в соответствии с формулой (4)) равно
Вернемся еще раз к экспоненциальной зависимости Непрерывное рассеяние энергии на сопротивлении приводит к тому, что наибольший заряд конденсатора уменьшается с каждым периодом колебаний, именно:
N- число колебаний. Этим амплитуды колебаний образуют убывающую геометрическую прогрессию. А это означает, что отношение величины каждого максимума
С логарифмическим декрементом затухания связана (обратно пропорциональной зависимостью) еще одна характеристика затухающих колебаний - добротность Q. (Не путать с зарядом q). Она определяется следующим образом:
то есть, чем меньше затухание, тем больше добротность. Для того, чтобы выявить смысл характеристик затухания, введем понятие времени релаксации Заменив t на Говорят Связь коэффициента затухания и логарифмического декремента получают из формулы определения последнего (10):
(Т- период колебаний). В случае слабого затухания можно выразить логарифмический декремент затухания через параметры контура
Таким образом, логарифмический декремент затухания есть величина, обратная числу колебаний, по происшествии которых амплитуда уменьшается в Исходя из формул (11) и (12), можно получить формулу зависимости добротности от параметров контура при слабом затухании:
Полная картина поведения электрического контура не ограничивается только затухающими колебаниями. В контуре с сильным затуханием (большим сопротивлением R) колебаний заряда нет, есть только монотонное убывание с течением времени. Не будем рассматривать соответствующие решения дифференциального уравнения (2). Заметим только, что специальный случай «критического затухания» имеет место при сопротивлении R, равном Эта последняя формула подтверждает общую особенность, выражающуюся в том, что все рассмотренные выше характеристики процессов в колебательном контуре имеют связи с численными значениями параметров контура R, L и С. Исследования, проводимые в этой работе, имеют целью проверить некоторые из них.
ПОДГОТОВКА К ВЫПОЛНЕНИЮ РАБОТЫ 1. Вписать формулы, определяющие зависимость периода Т затухающих колебаний от параметров контура R, L, С. 2. Вывести формулу зависимости логарифмического декремента затухания 3. Рассчитать величины периода колебаний Т и логарифмического декремента затухания 4. Ознакомиться с заданием лабораторного исследования (см. ниже) и составить таблицы записи результатов измерений и расчетов таким образом, чтобы можно было сравнить экспериментальные и расчётные данные.
ОПИСАНИЕ УСТАНОВКИ Электрическая цепь собрана по схеме, изображенной на рисунке 1. Колебания возбуждаются в контуре благодаря зарядке конденсатора от источника однополупериодного переменного тока с частотой 50 Гц. Затухающие колебания напряжения В качестве элементов колебательного контура используются наборы конденсаторов, катушек индуктивности и сопротивлений (резисторов). Присоединение каждого элемента набора производится с помощью кнопочного выключателя. Для включения элементов R,L, С в цепь контура нужно нажать соответствующие кнопки и зафиксировать их в «утопленном состоянии».
Рисунок 4 Значения сопротивления R, электроемкости С и индуктивности L для каждого положения кнопочных выключателей составляет отдельную таблицу. Таблица выдается на рабочее место при выполнении работы. Основные измерения проводятся с помощью осциллографа. Осциллограмма напряжения С основными органами управления осциллографом следует ознакомиться перед началом измерений.
ЗАДАНИЯ НА ЛАБОРАТОРНЫЕ ИССЛЕДОВАНИЯ И РАСЧЕТЫ Задание 1 Определить сопротивление 1. Включить источники напряжения и осциллограф. 2. Ввести в цепь контура конденсатор и наименьшей электроемкостью С, катушки индуктивности с индуктивностью в пределах L= (10÷100) мГн. Набор сопротивлений оставить выключенным. При этом цепь контура будет замкнутой, а сопротивление равно 3. Получить на экране осциллографа такую осциллограмму, в которой можно выделить две амплитуды колебаний U, отличающиеся (по вертикальным делениям сетки) в 2,7 раза (число 4. Используя обратную зависимость времени релаксации и коэффициента затухания:
Задание 2
|
||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 492; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.125.2 (0.036 с.) |

 а также характеристики электрического поля конденсатора.
а также характеристики электрического поля конденсатора. (1)
(1) или
или  - так обозначается производная по времени.
- так обозначается производная по времени.

 ,
,  ,
,  ,
,  будем называть пока просто постоянными величинами. Первая и вторая производные этой функции равны
будем называть пока просто постоянными величинами. Первая и вторая производные этой функции равны
 Подставив выражения производных в уравнение(2) сократив на множитель
Подставив выражения производных в уравнение(2) сократив на множитель  , получим
, получим (4)
(4) убывает со временем. Быстрота убывания определяется величиной
убывает со временем. Быстрота убывания определяется величиной  , которую называют коэффициентом затухания. Круговая частота
, которую называют коэффициентом затухания. Круговая частота  (4). Так как
(4). Так как  не может быть отрицательным, то затухающие колебания имеют место только при условии (см.4):
не может быть отрицательным, то затухающие колебания имеют место только при условии (см.4): , а величины
, а величины  от времени. Эта зависимость называется еще экспоненциальной.
от времени. Эта зависимость называется еще экспоненциальной.
 . Так как
. Так как  , то после дифференцирования получим:
, то после дифференцирования получим:
 как и складывая оба слагаемых выражения в скобках с помощью векторной
как и складывая оба слагаемых выражения в скобках с помощью векторной
 не зависит от характеристик затухания.
не зависит от характеристик затухания. реализуется неравенство:
реализуется неравенство:  . Это случай слабого затухания, величина сдвига фаз Ψ стремится к -
. Это случай слабого затухания, величина сдвига фаз Ψ стремится к -  (
( ). Например, для графиков (рисунок 2) отношения
). Например, для графиков (рисунок 2) отношения  составляет 0,03 и 0,064. Соответственно этому Ψ отличается от
составляет 0,03 и 0,064. Соответственно этому Ψ отличается от  .
. с помощью соотношения:
с помощью соотношения:
 =0,03 будет
=0,03 будет  =0,02%, а при
=0,02%, а при  =0,064 отличие частот составит 0,2%. На рисунке 2 оба колебания выглядят как колебания, имеющие одинаковые частоты.
=0,064 отличие частот составит 0,2%. На рисунке 2 оба колебания выглядят как колебания, имеющие одинаковые частоты. определяется в этом случае известной формулой Томсона:
определяется в этом случае известной формулой Томсона:  .
. (9)
(9) , изображенной на рисунке 2, чтобы рассказать о других важных характеристиках затухающих колебаний и дать им физическое объяснение.
, изображенной на рисунке 2, чтобы рассказать о других важных характеристиках затухающих колебаний и дать им физическое объяснение.
 к последующему
к последующему  (t+T) одинаково. Безразмерная величина, равная натуральному логарифму отношения амплитудных значений, отстоящих по времени на период колебания, называется логарифмическим декрементом затухания:
(t+T) одинаково. Безразмерная величина, равная натуральному логарифму отношения амплитудных значений, отстоящих по времени на период колебания, называется логарифмическим декрементом затухания: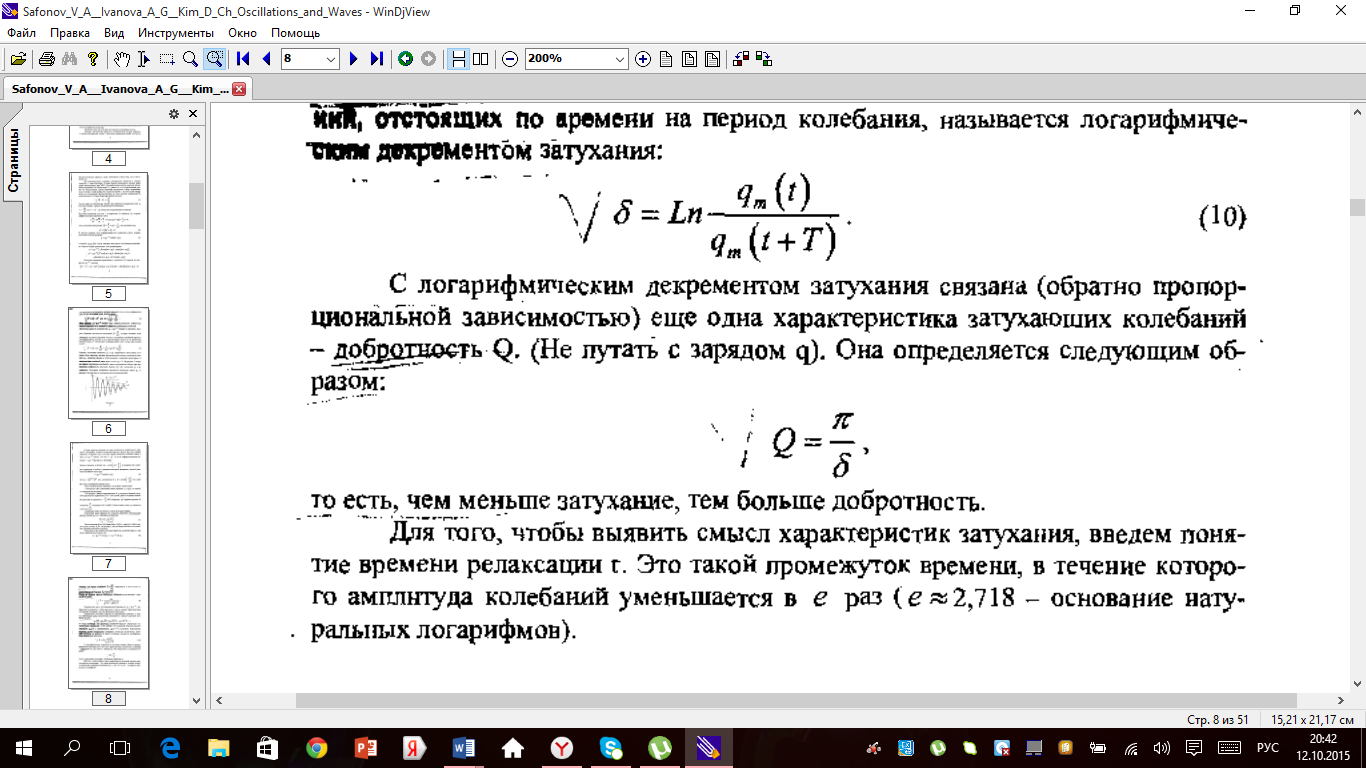 (10)
(10) , (11)
, (11) . Это такой промежуток времени, в течение которого амплитуда колебаний уменьшается в
. Это такой промежуток времени, в течение которого амплитуда колебаний уменьшается в  раз (
раз ( 2,718- основание натуральных логарифмов).
2,718- основание натуральных логарифмов). , получим
, получим  , откуда
, откуда  .
.
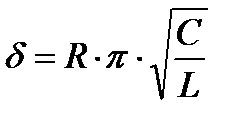 (12)
(12) - число колебаний, совершающихся в контуре за время, равное времени релаксации
- число колебаний, совершающихся в контуре за время, равное времени релаксации  ) добротность равна Q=18.
) добротность равна Q=18. (13)
(13) , в котором величину
, в котором величину  называют критическим сопротивлением контура.
называют критическим сопротивлением контура. от параметров контура в случае слабого затухания колебаний.
от параметров контура в случае слабого затухания колебаний. на конденсаторе подаются на клеммы вертикального усиления осциллографа (рисунок 3). При этом частоту развертки электрического сигнала осциллографом устанавливают примерно такой же, что и частота зарядки С.
на конденсаторе подаются на клеммы вертикального усиления осциллографа (рисунок 3). При этом частоту развертки электрического сигнала осциллографом устанавливают примерно такой же, что и частота зарядки С.

 выглядит так, как показано на рисунке 4, то есть подобна графику колебаний заряда на конденсаторе из рисунка 2 (
выглядит так, как показано на рисунке 4, то есть подобна графику колебаний заряда на конденсаторе из рисунка 2 ( ). Время по горизонтальной оси можно рассчитать. Для этого поверх экрана нанесена прямоугольная сетка, калиброванная в единицах времени (мс или мкс). Назовем временную длительность одного квадрата сетки по горизонтали ценой деления развертки и обозначим ее
). Время по горизонтальной оси можно рассчитать. Для этого поверх экрана нанесена прямоугольная сетка, калиброванная в единицах времени (мс или мкс). Назовем временную длительность одного квадрата сетки по горизонтали ценой деления развертки и обозначим ее  . Тогда время t, в течение которого происходят N колебаний, будет равно
. Тогда время t, в течение которого происходят N колебаний, будет равно  , где n- число квадратов сетки, в пределах которых укладываются эти N колебаний. На рисунке 4 видно, что для N=3, то есть для трех периодов Т, число n равно 12. Величину
, где n- число квадратов сетки, в пределах которых укладываются эти N колебаний. На рисунке 4 видно, что для N=3, то есть для трех периодов Т, число n равно 12. Величину  проводов намотки катушек индуктивности.
проводов намотки катушек индуктивности.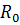 провода намотки включенных катушек индуктивности.
провода намотки включенных катушек индуктивности. ). Затем отсчитывают интервал времени, разделяющий эти две амплитуды. В горизонтальных делениях сетки интервал равен
). Затем отсчитывают интервал времени, разделяющий эти две амплитуды. В горизонтальных делениях сетки интервал равен  – цена деления, n- число делений). А по смыслу затухания колебаний- это время релаксации
– цена деления, n- число делений). А по смыслу затухания колебаний- это время релаксации  . Итак,
. Итак,  .
. и обозначение
и обозначение  в уравнении (2), получим формулу для расчета сопротивления
в уравнении (2), получим формулу для расчета сопротивления  . Вычисления выполнить в системе единиц СИ.
. Вычисления выполнить в системе единиц СИ.


