
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механика, электродинамика, колебанияСтр 1 из 9Следующая ⇒
В.М. Астахов, В.И. Машанов, И.В. Грищенко, А.Г. Иванова Методические указания к лабораторным работам 1 семестра
МЕХАНИКА, ЭЛЕКТРОДИНАМИКА, КОЛЕБАНИЯ Новосибирск СОДЕРЖАНИЕ
Лабораторная работа 1.2 ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА ОСНОВЕ МАЯТНИКА ОБЕРБЕКА ЦЕЛЬ РАБОТЫ Изучить законы вращательного движения. Определить собственный момент инерции маятника Обербека (крестовины). Исследовать зависимость момента инерции грузов на крестовине от расстояния.
ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ Законы вращательного движения проверяются на установке, называемой маятником Обербека‚ который представляет собой крестовину, вращающуюся вокруг горизонтальной оси (рис. 2). На шкив радиуса
Рис. 2
ПОДГОТОВКА К ВЫПОЛНЕНИЮ РАБОТЫ
Перед выполнением лабораторной работы необходимо установить основные физические закономерности, наблюдаемые на маятнике Обербека. Исходя из основного закона динамики вращательного движения (1), график зависимости углового ускорения от момента силы, приложенной к маятнику, должен представлять собой прямую линию. Второй закон Ньютона, применимый к описанию движения подвеса
Вращение маятника вызывает сила натяжения нити. Ее находим из
а момент силы натяжения нити:
Если подвес падает из неподвижного положения с высоты
где Поскольку нить намотана на шкив, то ускорение движения подвеса, равное ускорению движения нити, является также тангенциальным ускорением для точек на ободе шкива. Тангенциальное ускорение при вращательном движении связано с угловым ускорением шкива формулой:
Построив график зависимости β от Мнат, получим прямую. Поскольку в основной закон динамики вращательного движения (1) входит равнодействующий момент сил, то прямая не будет проходить через начало координат. Она будет смещена по оси момента сил на величину момента силы трения.
Момент инерции маятника Обербека определится из уравнения (1) как:
Исходя из формулы (2), момент инерции материальной точки прямо пропорционален квадрату расстояния от точки до оси вращения. Если считать грузы на спицах крестовины материальными точками, то график зависимости момента инерции грузов от квадрата расстояния до оси вращения должен быть линейным. Поскольку момент инерции тела – величина аддитивная, то момент инерции маятника с грузами J равен сумме момента инерции крестовины J0 и момента инерции грузов Jгр. Отсюда момент инерции грузов равен:
ЗАДАНИЕ
5. Постройте график зависимости углового ускорения маятника от момента силы натяжения нити.
Таблица1
II часть работы:
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА 1. Савельев И. В. «Курс физики», т.1, гл. КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Вывести формулу основного закона динамики вращательного 2. Провести аналогию между параметрами кинематики и динамики З. Какое движение называется вращательным? Приведите примеры. В каких случаях размером тел при рассмотрении законов движения можно пренебречь. 4. Дайте определение момента инерции твердого тела. Расскажите о теореме Штейнера. 5. Как в данной работе определить момент инерции маятника Обербека без грузов? 6. Как в данной работе можно определить массу грузов на стержнях маятника Обербека? 7. Как можно изменить момент инерции маятника Обербека? 8. Если увеличить высоту опускания подвеса, то какие величины изменяются и как (момент инерции маятника, время опускания подвеса, кинетическая энергия системы маятник-груз, угловое ускорение маятника)?
ЗАДАЧИ (нумерация задач: первая цифра- номер бригады, вторая цифра- номер задачи) 1.1. Найти линейную скорость Земли при ее движении по орбите. Средний радиус земной орбиты 1.2. Человек находится на краю круглой горизонтальной платформы радиусом 4 м. Сколько оборотов в минуту должна делать платформа вокруг вертикальной оси, чтобы человек мог удержаться на ней при коэффициенте трения 2.1. Найти угловую скорость ω: а) часовой стрелки на часах; б) минутной стрелки на часах. (145,4 10 -6 рад\с; 1,74 10 -6 рад\с). 2.2. Совершает ли работу равнодействующая всех сил, приложенных к телу, равномерно движущемуся по окружности? 3.1. Найти угловую ω и линейную скорости v вращения земной поверхности на экваторе. Радиус Земли Rз= 6,4 10 6 м. (72,7 10 -6 рад\с; 465,3 м\с). 3.2. Мотоциклист едет по горизонтальной дороге со скоростью 74 4.1 Определить момент инерции сплошного однородного диска массой m и радиусом R относительно оси, проходящей через точку на краю диска перпендикулярно его плоскости. (1,5 mR2). 4.2 Колесо, вращаясь равноускоренно по часовой стрелке, достигло угловой скорости 30 рад\с через 10 оборотов после начала вращения. Найти угловое ускорение β колеса. Показать на рисунке направление углового ускорения. (7,2 рад\с2). 5.1 Диск совершает 70 5.2 Точка движется по окружности 6.1 Найти радиус вращающегося колеса, если известно, что линейная скорость точки на ободе в 3 раза больше линейной скорости точки, лежащей на расстоянии 4 см ближе к оси колеса. (6см).
6.2 Определить момент инерции сплошного однородного диска массой 1кГ и радиусом 50 см относительно оси, проходящей через середину радиуса диска перпендикулярно его плоскости. (0,19 кг м2).
Работа 3.1 ЦЕЛЬ РАБОТЫ
1. Изучить основные электроизмерительные приборы, определить их основные характеристики, освоить методику измерения с помощью этих приборов. 2. Используя амперметр и вольтметр, определить величину неизвестного сопротивления.
Класс точности Любой электроизмерительный прибор дает при измерении некоторую погрешность. Пусть
определяет абсолютную погрешность измерения прибора. Относительной погрешностью называется отношение:
Все электроизмерительные приборы снабжены указателем класса точности, обычно это жирные цифры на шкале прибора, разделенные запятой. Класс точности соответствует приведенной погрешности прибора (γ):
и определяет максимальную абсолютную погрешность прибора
В приведенных формулах Ат — максимально возможное показание прибора. Ясно, что при малом отклонении стрелки прибора точность измерения уменьшается. Для повышения точности рекомендуется проводить измерения таким образом, чтобы стрелка находилась во второй половине шкалы прибора. Пример Вольтметр со шкалой 200 В, класс точности 2,0, при измерении дает показание 80 В. Максимальная абсолютная погрешность прибора, связанная сего классом точности, в соответствии с формулой (4), равна:
Относительная погрешность (2) равна:
Результат измерения записывается так:
Пример При измерении напряжения, равного 2,5В, стрелка прибора переместилась на 50 делений. Следовательно чувствительность прибора равна S=50/2,5=20 дел/В, а цена делений — С=1/20=0,05 В/дел.
Пределы измерений Значение измеряемой величины, при котором стрелка прибора отклонится до конца шкалы, называется пределом измерения. Электроизмерительные приборы могут иметь несколько пределов измерений (многопредельные приборы), осуществляемых с помощью переключателя пределов. НЕОБХОДИМО ПОМНИТЬ, что цена деления многопредельных приборов на различных пределах измерений — различна.
Многопредельность амперметра достигается его шунтированием. Шунт — дополнительное сопротивление, подключаемое параллельно к амперметру (Рис. 1).
Рис. 1 При шунтировании только часть измеряемого тока I течет через амперметр (IА), остальной ток идет через шунт. Пусть надо измерить ток I в n раз больший, чем максимально допустимый через прибор ток (Рис. 1). Здесь RA — внутреннее сопротивление амперметра. Определим сопротивление шунта RШ, пользуясь законом Ома. Напряжение на шунте и амперметре одинаково, т. к. они соединены параллельно:
Полный ток в цепи равен сумме токов:
По условию требуется, чтобы:
Окончательно находим:
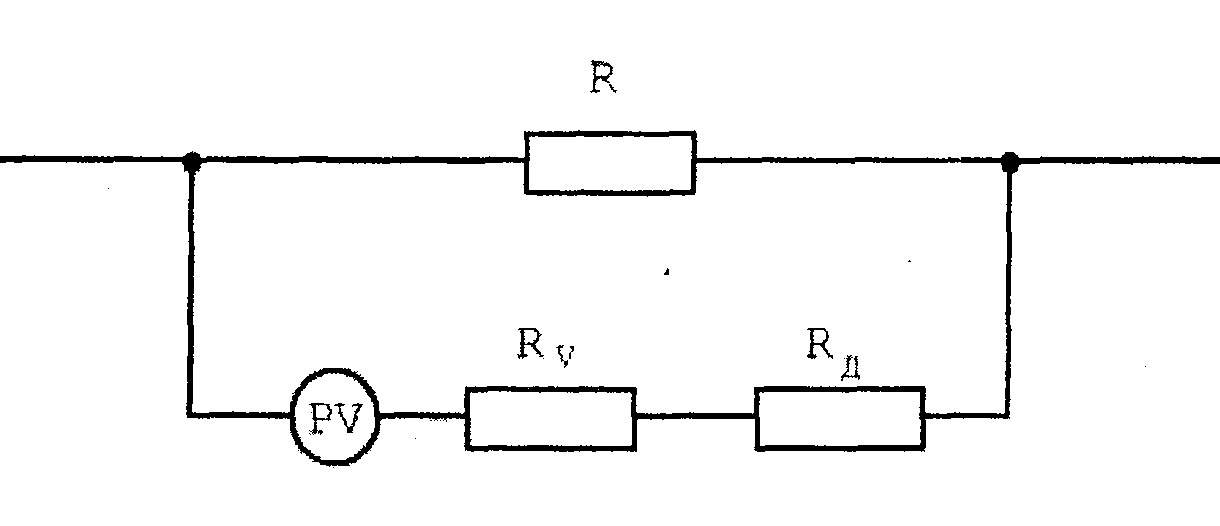
Следовательно, для увеличения предела измерения в n раз сопротивление шунта должно быть в (n - 1) раз меньше сопротивления амперметра. Предел измерения вольтметра изменяют с помощью дополнительного сопротивления RД, подключаемого последовательно к вольтметру (Рис. 2).
Рис. 2 Здесь Rv — внутреннее сопротивление вольтметра, R — сопротивление нагрузки, на котором измеряется напряжение. Для того, чтобы измерить с помощью вольтметра напряжение, в n раз превышающее максимально измеряемое вольтметром, нужно подключить дополнительное сопротивление, равное:
Эта формула может быть получена из соображений, аналогичных при рассмотрении шунтирующего сопротивления к амперметру. Следовательно, для увеличения предела измерения вольтметра в n раз, последовательно к нему нужно подключить дополнительное сопротивление в (n -1) раз большее внутреннего сопротивления вольтметра. Рассмотрим простой метод определения сопротивления проводника с помощью вольтметра и амперметра. Измеряя величину тока, протекающего по сопротивлению, и напряжение на нем, по закону Ома:
можно рассчитать величину сопротивления. Для повышения точности обычно проводится несколько измерений и строится график зависимости силы тока от напряжения (вольтамперная характеристика сопротивления), (Рис.3). Через экспериментальные точки на графике проводится оптимальная прямая (графическое усреднение результатов). В соответствие с (11) тангенс угла наклона этой прямой с осью абсцисс равен величине, обратной среднему значению сопротивления (Rизм):
Рис. 3 Оценим погрешность определения сопротивления, считая, что она обусловлена лишь случайными факторами. Относительная погрешность сложной функции равна (смотрите Приложение 4):
Абсолютные погрешности при измерении силы тока и напряжения определяются классом точности приборов. В качестве I и U в формуле (12) можно взять наибольшие измеренные величины, если экспериментальные точки отклоняются от прямой не более чем на
ПОДГОТОВКА К ВЫПОЛНЕНИЮ РАБОТЫ 3.1 Изучите материал методических указаний и литературу: [1] — §34, [2] — §33. 3.2 Заготовьте в отчет две таблицы измерений.
Таблица 1 Изучение электроизмерительных приборов
Таблица 2 Определение сопротивления резистора
ЗАДАНИЕ 5.1 По указанию преподавателя изучите приборы на рабочем месте и данные занесите в таблицу 1. Обратите внимание на пределы измерения прибора. 5.2 Вместе с преподавателем подключите сопротивление к регулируемому низковольтному источнику напряжения согласно схеме Рис. 3 и самостоятельно выберите пределы измерения вольтметра и амперметра. 5.3 Исследуйте зависимость силы тока от напряжения на сопротивлении, данные занесите в таблицу 2. Для этого плавно увеличивайте напряжение, начиная с нуля, на равные величины и измеряйте соответствующие значения силы тока. Экспериментальных точек должно быть не менее 10. 5.4 Постройте график зависимости силы тока от напряжения на сопротивлении. Через экспериментальные точки проведите прямую таким образом, чтобы максимальное количество точек оказалось на прямой, и по формуле (11) рассчитайте сопротивление. 5.5 Оцените погрешности определения сопротивления по формулам (12) и (13) и запишите конечный результат в виде:
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Нарисуйте схемы подключения к измеряемой цепи амперметра и вольтметра. 2. Каким условием должны удовлетворять внутренние сопротивления амперметра и вольтметра? 3. Вольтметром на 15 В (класс точности 1,0) измерено напряжение 6,0 В. Каковы абсолютная и относительная погрешности измерения? 4. Определите цену деления и чувствительность амперметра на 30 мА, шкала которого имеет 500 делений. 5. Можно ли использовать миллиамперметр на 10 мА для измерения силы тока 10 А? Внутреннее сопротивление прибора 50 (Ом). 6. Проанализируйте возможные погрешности при измерении сопротивления по схеме Рис. 4. Объясните формулу относительной погрешности (12). ЛИТЕРАТУРА 1. Савельев И. В. Курс обшей физики, 1978, т. 2. 2. Савельев И. В. Курс обшей физики, 1973, т. 2. ЗАДАЧИ (нумерация задач: первая цифра- номер бригады, вторая цифра- номер задачи) 1.1. Амперметр с сопротивлением Ra=0.16Ом зашунтирован сопротивлением R = 0.04Ом. Амперметр показывает ток I0 = 8А. Найти ток I в цепи. (40А). 1.2. Гальванический элемент с ЭДС ε=1,5 B и внутренним сопротивлением 1 Ом замкнут на внешнее сопротивление 4 Ом. Найти силу тока в цепи и падение напряжения на внешнем сопротивлении. (0,3 А; 1,2 В). 2.1. Внутреннее сопротивление источника питания в n раз меньше внешнего сопротивления R, на который замкнут источник с ЭДС ε. Найти силу тока в цепи и падение напряжения на внешнем сопротивлении. (ε n\(n+1)R; ε n\(n+1)). 2.2. Вывести формулу для определения шунта вольтметра и применить ее для решения следующей задачи. Вольтметр с внутренним сопротивлением 2500 Ом показывает напряжение 125 В. Определить дополнительное сопротивление, при подключении которого вольтметр показывает 100 В. (500 Ом). 3.1. Два одинаковых источника тока (ε=1,5 В, r= 0,4 Ом) соединены параллельно и замкнуты на внешнее сопротивление 1 Ом. Определить силу тока в цепи. (1,2 А). 3.2. Два одинаковых источника тока (ε=1,5 В, r= 0.4 Ом) соединены последовательно и замкнуты на внешнее сопротивление 1 Ом. Определить силу тока в цепи. (1,7 А). 4.1. Миллиамперметр предназначен для измерения силы тока не более 10 мА. Что нужно сделать, чтобы миллиамперметр можно было использовать для измерения токов до 1 А? Внутреннее сопротивление прибора 9,9 Ом. (0,1 Ом). 4.2. Шесть элементов с ЭДС ε=1,5 В и внутренним сопротивлением 0,4 Ом каждый, соединены в батарею так, что по нагрузке R=0,2 Ом протекает ток 5.6 А. Как соединены элементы? (параллельно). 5.1. Вольтметр имеет сопротивление 200 Ом. Последовательно с ним включено дополнительное сопротивление 1000 Ом. Во сколько раз увеличилась цена деления вольтметра? (в 6 раз). 5.2. Найти падение потенциала в сопротивлениях R1, R2 и R3 (Рис.а) и токи I2 и I3 в сопротивлениях R2 и R3 если через цепь протекает ток I1 = 3 А. Сопротивления R1=R2=4 Ом, R3=2 Ом. (U1 = 12В, U2 = U3 = 4В, I2 = 1 А, I3 = 2 А).
Рис. а Рис. б Рис. в 6.1. Вычислить сопротивление проволочного куба, если он включен в электрическую цепь, как показано на рис. б. Сопротивление каждого ребра куба равно 1 Ом. (5\6 Ом). 6.2. Найти сопротивление R1 (Рис.в), а также токи I2 и I3 в сопротивлениях R2 и R3 если через цепь протекает ток I = 3 А. Сила тока через сопротивление R1 равна I1 = 1 А. Сопротивления R2=4 Ом, R3=2 Ом. (R1 = 6,8 Ом, I2 = 1,7 А, I3 = 3,3 А). Работа 3.2 ИЗУЧЕНИЕ ХАРАКТЕРИСТИК ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
ЦЕЛЬ РАБОТЫ Исследовать электростатическое поле, графически изобразить сечение эквипотенциальных поверхностей и силовые линии для некоторых конфигураций поля.
ПОДГОТОВКА К ВЫПОЛНЕНИЮ РАБОТЫ Перед выполнением работы следует изучить следующие вопросы: 3.1 Электрическое поле и его характеристики: напряженность и потенциал. Графическое изображение поля. Эквипотенциальные поверхности. [1] — §5, 6, 8, [2] — §5, 7, 10, 12. 3.2 Работа по перемещению заряда в электрическом поле. Связь между напряженностью и потенциалом электрического поля. [1] — § 8, [2] — §9, 11. 3.3 Теорема Гаусса для электростатического поля. [1] — §13, [2] — §8. 3.4 Проводник в электрическом поле. Поле внутри замкнутой проводящей оболочки, помещенной в электрическое поле. Экранирование. [1 ] — §25, 26, [2] — §21,22.
ЗАДАНИЕ В работе требуется получить графическое изображение электростатического поля при различных положениях электродов. Для этого на тетрадном листе начертите сечение ванны и разграфите его, как и дно ванны, укажите расположение электродов. Размер ванночки, форму и размер электродов предпочтительно рисовать в масштабе 1:1. Затем, после выполнения указанных ниже операций, нанесите на этот лист сечения эквипотенциальных поверхностей и силовые линии поля. 4.1 Подключите установку с закрепленными, погруженными в воду электродами к источнику постоянного напряжения (левая часть стенда), согласно Рис. 4. 4.2 Установите предел измерения вольтметра — 10 В. Подайте на электроды напряжение 10 В и переключите вольтметр на режим работы с зондом. 4.3 Прижмите зонд к дну ванны — вольтметр должен показать напряжение между одним из электродов и данной точкой. Принимая потенциал этого электрода за нуль, с помощью вольтметра определите потенциал данной точки. 4.4 Перемещая зонд по дну ванны, найдите точку с потенциалом 1-2 В. Затем перемещая зонд на небольшое, порядка 1 см, расстояние, найдитесоседнюю точку с таким же потенциалом и так далее. Определенные такимобразом точки перенесите на приготовленный лист, соедините точкилиниями и подпишите значения потенциала. Аналогичные измеренияпроделайте для потенциалов 3,... 9 В. Эквипотенциальные линии должныначинаться и кончаться у краев ванны. 4.5 В ванну положите замкнутый проводник в виде прямоугольника или круга и проведите измерения, указанные в пункте 5.4. Затем исследуйте поле снаружи и внутри замкнутого проводника. Результаты измерения изобразите на новом листе. 4.6 На листах с изображением эквипотенциальных линий нанесите силовые линии поля с учетом масштаба. Оцените в нескольких точках с помощью формулы (14) величину напряженности электрического поля. Укажите полярность электродов.
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Дайте определения электростатического поля и его характеристик. 2. Изобразите силовые линии и эквипотенциальные линии поля точечного заряда. 3. Оцените величину силы, действующую на электрон, помещенный в некоторую точку вашего исследуемого поля. 4. Рассчитайте работу по перемещению электрона между двумя точками в исследуемом поле. 5. Сформулируйте теорему Гаусса для электростатического поля. 6. С помощью теоремы Гаусса и формулы (14) докажите, что потенциал внутри замкнутого проводника, помещенного в электрическое поле, постоянен. 7. С помощью теоремы Гаусса рассчитайте электрическое поле равномерно заряженных нити и плоскости ЛИТЕРАТУРА 1. Савельев И.В. Курс общей физики, том 2, 1978. 2. Савельев И.В. Курс общей физики, том 2, 1970.
ЗАДАЧИ (нумерация задач: первая цифра- номер бригады, вторая цифра- номер задачи) 1.1. Два точечных заряда, находясь в воздухе ( r1=20 см друг от друга, взаимодействуют с некоторой силой. На каком расстоянии r2 нужно поместить эти заряды в масле ( 1.2. Найти отношение силы гравитационного притяжения между двумя протонами к силе их электростатического отталкивания. Заряд протона равен по модулю и противоположен по знаку заряду электрона (е=1.6 10-19 К). Масса протона равна 1840 me, (me.= 9.1 10-31 кГ). Гравитационная постоянная 2.1. Найти напряженность Е электрического поля в точке, лежащей посередине между точечными зарядами q1=8 нКл и q2=-6 нКл. Расстояние между зарядами r=10см, 2.2. Найти скорость электрона, прошедшего разность потенциалов 100 В. (5,9 10 6 м\с). 3.1. В центр квадрата, в каждой вершине которого находится заряд q=3 нКл, помещен отрицательный заряд q0. Найти этот заряд, если на каждый заряд q действует результирующая сила F= 0. (q0=-2,85нКл). 3.2. Найти силу F, действующую на заряд q= 2 нКл, если заряд помещен на расстоянии r =2 см от поверхности заряженного шара с радиусом R=2 см и поверхностной плотностью заряда проницаемость среды 4.1. Найти силу F, действующую на заряд q=2 нКл, если заряд помещен на расстоянии r=2см от заряженной нити с линейной плотностью заряда
4.2. Найти силу F, действующую на заряд q =2 нКл, если заряд помещен на расстоянии r = 2 см в поле заряженной плоскости с поверхностной плотностью заряда 5.1. На расстоянии 8 см друг от друга в воздухе находятся два заряда по 1 нКл. Определить напряженность и потенциал поля в точке, находящейся на расстоянии 5 см от зарядов. (4,3 кВ\м; 360 В). 5.2. На металлической сфере радиусом 15 см находится заряд q=4 нКл. Определите напряженность Е электростатического поля на расстоянии r=10 см от центра сферы и на поверхности сферы. (0; 1,6 кВ\м) 6.1. Два заряда находятся в керосине ( 6.2. В вершинах квадрата со стороной 5 см находятся одинаковые положительные заряды q=10нКл. Определите напряженность электростатического поля: 1) в центре квадрата; 2) в середине одной из сторон квадрата. (0; 51,5 кВ\м).
Работа 3.3 ЦЕЛЬ РАБОТЫ
1. Исследовать вольтамперные характеристики вакуумного диода. 2. Определить работу выхода электронов из материала катода вакуумного диода.
ПОДГОТОВКА К ВЫПОЛНЕНИЮ РАБОТЫ Перед выполнением работы необходимо изучить следующие вопросы:
3.1 Современные представления о строении металлов: [1] — §71, [2] — §60. 3.2 Работа выхода электрона: [1] — §74, [2] — §60. 3.3 Термоэлектронная эмиссия. Вольтамперная характеристика вакуумного диода: [1] — §75, [2] — §61. 3.4 Зависимость сопротивления проводников от температуры: [1] — §33, [3] — §34. 3.5 Приготовить две таблицы для измерения вольтамперных характеристик.
ЗАДАНИЕ 5.1 Установите следующие пределы измерения прибора: цепь накала: амперметр– 200мА, вольтметр– 10В; анодная цепь: амперметр – 1 ÷2 мА, вольтметр – 200 В. ВНИМАНИЕ! АНОДНЫЙ ТОК НЕ ДОЛЖЕН ПРЕВЫШАТЬ 2 мА! 5.2 Задайте катодное напряжение 8В и проверьте, есть ли при этом напряжении анодный ток. Если тока нет, добавьте 0,5В на цепь катода, и вновь проверьте анодный ток. 5.3 Снимите ВАХ диода, данные занесите в таблицу. Для этого изменяйте анодное напряжение через каждое деление для остального анализа возрастания тока, и через 40В, когда анодный ток выходит в режим насыщения. 5.4. Увеличьте накал катода не более, чем на 1В и повторите процедуру снятия ВАХ. 5.5 По экспериментальным данным постройте графики ВАХ, аналогичные Рис. 3 Из графиков определите величины токов насыщения. 5.6 С помощью закона Ома определите сопротивление катода при различных температурах (4). 5.7 Рассчитайте температуры катода Т1 и Т2. В нашей работе R0=3Ом, для вольфрама α=5,1·10-3К-1. 5.8 С помощью формулы (6) рассчитайте работу выхода электрона из вольфрама. 5.9 Оцените погрешности полученной величины А.
6. КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Расскажите о модели свободных электронов в металле. 2. Объясните энергетическую диаграмму на Рис. 1. 3. Дайте определение работы выхода электрона. От каких факторов она зависит? 4. Проанализируйте ВАХ диода в основных точках зависимости. 5. Укажите основное свойство вакуумного диода. В каких практических целях используется диод? 6. Приведите вывод расчетной формулы (4). 7. Объясните зависимость сопротивления металла от температуры. ЛИТЕРАТУРА 1. Савельев И.В. Курс общей физики, 1970, т.2. 2. Савельев И.В. Курс общей физики, 1982, т.3. 3. Савельев И.В. Курс общей физики, 1978, т.2.
ЗАДАЧИ (нумерация задач: первая цифра- номер бригады, вторая цифра- номер задачи) 1.1. Вычислить ток насыщения для вакуумного диода с вольфрамовым катодом при температуре катода Т = 1000К. Работа выхода электронов из вольфрама равна А = 4,5эВ, константа диода составляет В=60 1.2. Вычислить, насколько изменится отношение величин токов насыщения при увеличении температуры вольфрамового катода с 1800К до 1900К. Работа выхода электронов из вольфрама равна А= 4,5эВ, постоянная Больцмана составляет k=1,38 10-23 2.1. Какой наименьшей скоростью v должен обладать электрон для того, чтобы ионизировать атом водорода? Потенциал ионизации атома водорода составляет U=13,5 В. (2,2 106 м\с). 2.2. При какой температуре Т атомы ртути имеют кинетическую энергию поступательного движения, достаточную для ионизации? Потенциал ионизации атома ртути составляет U = 10,4 B (Wкин = 3.1. Потенциал ионизации атома гелия составляет U=24,5В. Найти работу ионизации А. (39, 2 10-19 Дж). 3.2. При повышении температуры с 300К сопротивление медного проводника возросло в два раза. До какой температуры был нагрет проводник? Термический коэффициент сопротивления меди α=4,2·10-3K-1. (838К). 4.1. Во сколько раз изменится ток насыщения вольфрамового катода при повышении температуры катода от 2400К на 100К? (2,6).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 477; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.108.186 (0.219 с.) |
 наматывается нить, к которой через блок прикреплен подвес. Подвес представляет собой цилиндр с прорезью для закрепления на нити. Подвес при опускании движется вдоль вертикальной линейки, на которой отмечаются начальная и конечная точки движения. С помощью секундомера фиксируется точное время движения между этими точками.
наматывается нить, к которой через блок прикреплен подвес. Подвес представляет собой цилиндр с прорезью для закрепления на нити. Подвес при опускании движется вдоль вертикальной линейки, на которой отмечаются начальная и конечная точки движения. С помощью секундомера фиксируется точное время движения между этими точками.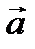
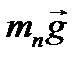


 , запишется как:
, запишется как: .
. ,
, . (6)
. (6)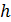 , то ускорение
, то ускорение  определится из закона равноускоренного движения:
определится из закона равноускоренного движения: , (7)
, (7) время опускания груза.
время опускания груза. (8)
(8) (9)
(9) (7)
(7) часть работы:
часть работы: измерьте высоту опускания подвеса
измерьте высоту опускания подвеса 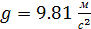
 , § 35, 36, 38, 39.
, § 35, 36, 38, 39.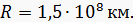 (4,5 10 4 м\с).
(4,5 10 4 м\с). = 0,27? (48,8 об\мин).
= 0,27? (48,8 об\мин). , делая поворот радиусом кривизны 100 м. На сколько при этом он должен наклониться, чтобы не упасть на повороте? (66,7°).
, делая поворот радиусом кривизны 100 м. На сколько при этом он должен наклониться, чтобы не упасть на повороте? (66,7°). . Где можно положить на диск тело, чтобы оно не соскользнуло? Коэффициент трения покоя
. Где можно положить на диск тело, чтобы оно не соскользнуло? Коэффициент трения покоя 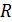 = 10 см с постоянным тангенциальным ускорением:
= 10 см с постоянным тангенциальным ускорением:  . Найти тангенциальное ускорение точки, если известно, что к концу пятого оборота после начала движения скорость точки стала
. Найти тангенциальное ускорение точки, если известно, что к концу пятого оборота после начала движения скорость точки стала  . (1,3 м2\с).
. (1,3 м2\с). — истинное значение измеряемой величины, А –показание прибора. Тогда разность:
— истинное значение измеряемой величины, А –показание прибора. Тогда разность:


 А, которая считается одинаковой для всех точек шкалы:
А, которая считается одинаковой для всех точек шкалы: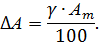
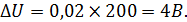

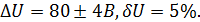










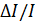 и
и  .Абсолютную погрешность при расчете сопротивления определим следующим образом:
.Абсолютную погрешность при расчете сопротивления определим следующим образом:



 1) на расстоянии
1) на расстоянии =5), чтобы получить ту же силу взаимодействия? (5,9 см).
=5), чтобы получить ту же силу взаимодействия? (5,9 см). (1,24 1026).
(1,24 1026). =1. (50,4 кВ\м).
=1. (50,4 кВ\м). . Диэлектрическая
. Диэлектрическая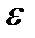 = 6, ε0 =8.85 10-12 Ф/м. (188 мкН).
= 6, ε0 =8.85 10-12 Ф/м. (188 мкН). . Диэлектрическая проницаемость среды
. Диэлектрическая проницаемость среды 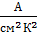 . (3,4 мА).
. (3,4 мА). , 1эВ=1,6 10-19 Дж. (5,1).
, 1эВ=1,6 10-19 Дж. (5,1). kT, k=1.38 10-23
kT, k=1.38 10-23 


