
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод максимальної правдоподібності
Одним із найбільш універсальних методів одержання оцінок параметрів розподілів генеральної сукупності є метод максимальної правдоподібності. Основу метода складає функція правдоподібності, яка виражає щільність імовірності (імовірність) сумісної появи результатів вибірки
Згідно з методом максимальної правдоподібності за оцінку невідомого параметра Природність такого підходу до визначення статистичних оцінок випливає із смислу функції правдоподібності, яка при кожному фіксованому значенні параметра Для одержання оцінки максимальної правдоподібності треба розв’язати рівняння:
Якщо потрібно оцінити не один, а декілька параметрів
Достоїнство методу максимальної правдоподібності полягає у тому, що для широкого класу розподілів він приводить до оцінок, які є слушними, асимптотично ефективними, мають асимптотично нормальний розподіл і, якщо для параметра Приклад 2.4. Методом максимальної правдоподібності оцінимо параметр Статистична модель. Генеральна сукупність має розподіл Пуассона.
де n – кількість випробувань у кожній серії, Розв’язання. Складемо функцію правдоподібності.
Визначимо логарифм цієї функції
Прирівнюючи похідну цієї функції по
Розв’язуючи це рівняння відносно
Оскільки
то
З вищенаведеного одержуємо, що Алгоритм у Mathсad Початкові дані
Моделювання вибірки об’єму
Фрагмент варіаційного ряду
Середнє значення
Оцінка параметра розподілу Пуассона
Приклад 2.5. Методом максимальної правдоподібності знайдемо оцінки параметрів Статистична модель. Вибірка Розв’язання. Записуємо логарифмічну функцію правдоподібності:
Диференціюючи
Звідки знаходимо оцінки:
Ці оцінки співпадають з оцінками методу моментів. Вони слушні, причому Алгоритм у Mathcad знаходження оцінок Метод найменших квадратів Сутність методу найменших квадратів полягає у тому, що оцінки невідомих параметрів розподілу
Використовуючи необхідну умову екстремуму функції, прирівнюємо до нуля похідну
Звідки
Отже, оцінка генеральної середньої є вибіркове середнє Метод найменших квадратів має широке застосування у практиці статистичних досліджень, оскільки, по-перше, не потребує знання закону розподілу вибіркових даних; по-друге, для нього досить добре розроблений математичний апарат чисельної реалізації. Метод найменших квадратів застосовується у моделях кореляційного і регресійного аналізу. 2.4.7. Метод мінімуму χ2
Статистична модель. Нехай Припустимо, що множина значень Х розбита на Позначимо через
яка служить оцінкою параметра Оцінка
За своїми асимптотичними властивостями оцінки, які визначаються за методом
Ця система еквівалентна системі
Дійсно
Розбиття гіпотетичного простору Х на
Отже, система рівнянь (2.34) еквівалентна системі рівнянь
|
||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 847; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.221.67 (0.021 с.) |
 :
: (2.30)
(2.30)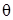 приймається таке його значення
приймається таке його значення  , яке максимізує функцію
, яке максимізує функцію  . Величина
. Величина 
 ,
,  , оскільки максимум обох функцій досягається при одному і тому ж значенні
, оскільки максимум обох функцій досягається при одному і тому ж значенні 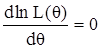 .
. , то оцінка максимальної правдоподібності цих параметрів знаходиться із системи рівнянь
, то оцінка максимальної правдоподібності цих параметрів знаходиться із системи рівнянь
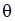 існує ефективна оцінка, то рівняння правдоподібності має єдиний розв’язок, який співпадає з нею. Однак оцінка максимальної правдоподібності може виявитись зсуненою.
існує ефективна оцінка, то рівняння правдоподібності має єдиний розв’язок, який співпадає з нею. Однак оцінка максимальної правдоподібності може виявитись зсуненою. розподілу Пуассона.
розподілу Пуассона.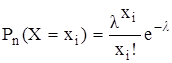 ,
, – кількість появ події у i-й серії
– кількість появ події у i-й серії  . Знайдемо оцінку
. Знайдемо оцінку 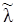 невідомого параметра
невідомого параметра  .
.
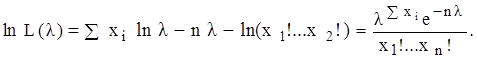
 .
.

 є точкою максимуму функції
є точкою максимуму функції  .
.

 із генеральної сукупності розподіленої за законом Пуассона з параметром
із генеральної сукупності розподіленої за законом Пуассона з параметром  і одержання варіаційного ряду
і одержання варіаційного ряду

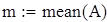

 ◄
◄ і
і  нормального розподілу.
нормального розподілу.
 по
по  одержуємо систему рівнянь:
одержуємо систему рівнянь: ,
, .
. ,
, 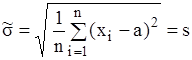 .
. є незсуненою, а
є незсуненою, а  – зсуненою і, як було сказано раніше,
– зсуненою і, як було сказано раніше, 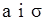 за методом максимальної правдоподібності аналогічний алгоритму для методу моментів, наведеному у прикладі 2.3. Значення оцінок:
за методом максимальної правдоподібності аналогічний алгоритму для методу моментів, наведеному у прикладі 2.3. Значення оцінок:  ◄
◄ визначаються із умови мінімізації суми квадратів відхилень вибіркових даних
визначаються із умови мінімізації суми квадратів відхилень вибіркових даних  від оцінки, що визначається. Наприклад, знайдемо оцінку за методом найменших квадратів
від оцінки, що визначається. Наприклад, знайдемо оцінку за методом найменших квадратів  . Згідно з цим методом оцінку
. Згідно з цим методом оцінку  (2.31)
(2.31)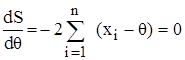 або
або 
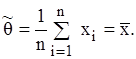 (2.32)
(2.32)
 – вибірка незалежних спостережень над випадковою величиною Х, розподіл якої належить класу розподілів
– вибірка незалежних спостережень над випадковою величиною Х, розподіл якої належить класу розподілів 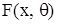 , який залежить від невідомого параметра
, який залежить від невідомого параметра  (можливо векторного –
(можливо векторного – 
 Вибірка одержана при деяких конкретних значеннях цього параметра.
Вибірка одержана при деяких конкретних значеннях цього параметра.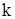 інтервалів
інтервалів  які не перетинаються. Позначимо через
які не перетинаються. Позначимо через  число спостережень у вибірці
число спостережень у вибірці  Якщо множина значень Х скінченна, тобто величина приймає лише скінченне число значень, то можна вважати, що
Якщо множина значень Х скінченна, тобто величина приймає лише скінченне число значень, то можна вважати, що  одноточкова множина. Таким чином, проведено групування результатів спостережень, у результаті чого одержано інтервальний варіаційний ряд.
одноточкова множина. Таким чином, проведено групування результатів спостережень, у результаті чого одержано інтервальний варіаційний ряд. імовірність попадання значень випадкової величини Х у
імовірність попадання значень випадкової величини Х у  -й інтервал. Визначимо величину
-й інтервал. Визначимо величину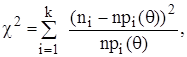 (2.33)
(2.33)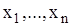 . Оскільки ймовірності
. Оскільки ймовірності  є функціями вибіркових значень, то і величина
є функціями вибіркових значень, то і величина 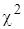 є функцією вибірки.
є функцією вибірки. називається оцінкою за методом
називається оцінкою за методом  -вимірний параметр, то для знаходження оцінки за методом мінімуму
-вимірний параметр, то для знаходження оцінки за методом мінімуму  (2.34)
(2.34) дуже близькі до оцінок максимальної правдоподібності. Наприклад, при деяких умовах з імовірністю 1 є лише один слушний корінь відповідних рівнянь і він дійсно дає абсолютний мінімум величини
дуже близькі до оцінок максимальної правдоподібності. Наприклад, при деяких умовах з імовірністю 1 є лише один слушний корінь відповідних рівнянь і він дійсно дає абсолютний мінімум величини  відносна частота
відносна частота  за ймовірністю збігається до ймовірності
за ймовірністю збігається до ймовірності  , тому другий член в (2.34) прямує до 0. Отже, систему рівнянь (2.34) можна замінити близькою до неї системою
, тому другий член в (2.34) прямує до 0. Отже, систему рівнянь (2.34) можна замінити близькою до неї системою
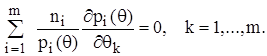 (2.35)
(2.35)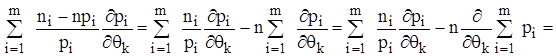

 , що не перетинаються, породжує дискретну випадкову змінну, функція правдоподібності якої є
, що не перетинаються, породжує дискретну випадкову змінну, функція правдоподібності якої є (2.36)
(2.36) (2.37)
(2.37)


