
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числові характеристики статистичних розподілів
Статистичний розподіл вміщує повну інформацію про варіацію ознаки. Однак велика кількість числових даних, за допомогою яких він задається, ускладнює їх використання. Між тим, при розв’язанні багатьох задач ця інформація виявляється надмірною і може бути з успіхом замінена невеликою кількістю звідних характеристик розподілу. Більш того, мистецтво статистичного аналізу якраз і визначається не безпосереднім використанням статистичного розподілу, а тим, наскільки успішно і повно вдається здійснити такий аналіз, спираючись на мінімальну кількість показників. Для опису статистичних розподілів використовуються три види характеристик (показників): ● середні або характеристики центральної тенденції; ● характеристики мінливості варіант; ● характеристики, які відображають додаткові особливості розподілів, зокрема їх форму. Усі вони обчислюються за результатами спостережень і побудованих у результаті їх первинної обробки статистичних розподілів. Тому їх називають статистичними. Розрахунок статистичних характеристик є другий після групування етап обробки даних спостережень. Цим, звичайно, не вичерпується статистичний аналіз, основною метою якого є встановлення загальних закономірностей змін ознаки. Однак, такий аналіз опирається на побудову теоретико-імовірнісної моделі і буде розглядатись у подальшому після підготовки необхідного математичного апарату. Середні величини Кожній числовій характеристиці випадкової величини Середня величина характеризує типовий для сукупності розмір ознаки або, як іноді говорять, центральну тенденцію у розподілі. Очевидно практичне використання такої характеристики доцільне у тому випадку, коли окремі варіанти ряду розподілу концентруються поблизу деякого значення. Якщо ж сукупність дуже неоднорідна, результати спостережень значно відрізняються один від одного і не виявляють загальної тенденції, її використання стає чисто формальним. Існують різні форми середніх. До вибору форми середнього слід підходити керуючись задачею дослідження і визначальною властивістю розподілу, яка повинна бути виражена цією характеристикою.
Основним видом середніх є середнє арифметичне. Ø Середнім арифметичним
де
Важливіша властивість середнього арифметичного – сума відхилень варіант від середнього значення дорівнює 0:
При розв’язанні практичних задач можуть застосовуватись і інші форми середнього – середнє геометричне і середнє гармонічне. Ø Емпіричним середнім геометричним
Середнє геометричне знаходить застосування при розрахунках темпів зміни величини, зокрема, у тих випадках, коли мають справу з величиною, зміни якої відбуваються приблизно у прямо пропорційній залежності з досягнутим до цього моменту рівнем самої величини, наприклад, рівнем доходу, або ж коли мають справу із середнім з відношень, наприклад, при розрахунках індексів цін. Ø Емпіричним середнім гармонічним
Гармонічне середнє значення ряду чисел завжди менше середнього геометричного значення тих же чисел, а тим більше – їх середнього арифметичного. Область його застосування досить обмежена. В економіці, зокрема, користуються іноді середнім гармонічним при аналізі середніх норм часу, а також у деяких видах індексних розрахунків. Окрім розглянутих середніх, які називаються аналітичними у статистичному аналізі, застосовують структурні або порядкові середні. Із них найбільш широко застосовуються медіана і мода. Ø Медіаною Ме варіаційного ряду називається значення ознаки, яке розділяє ранжовану сукупність на дві рівні за чисельністю групи: перша містить варіанти із значеннями меншими Me, друга – зі значеннями варіант більшими Me. Із означення емпіричної функції розподілу (накопиченої частоти) випливає, що:
Для дискретного варіаційного ряду з непарним числом членів медіана дорівнює середньому члену, а для ряду з парним числом членів – півсумі двох середніх членів. Для інтервального варіаційного ряду знаходиться медіанний інтервал
де Зазначимо, що медіана може бути приблизно визначена за допомогою емпіричної функції розподілу Ø Модою Mo варіаційного ряду називається значення варіанти, якій відповідає найбільша частота. У багатьох випадках мода є найбільш характерною для ряду розподілу і навколо неї концентрується більша частина варіант. При зміні крайніх членів ряду мода не змінюється, тобто вона має певну сталість до варіації ознаки. Тому її особливо зручно застосовувати при дослідженні рядів з невизначеними границями. Моду доцільно застосовувати також і в тому випадку, коли при вивченні варіації ознаки важко визначити одну превалюючу над усіма іншими частоту. Для дискретного варіаційного ряду мода знаходиться безпосередньо за означенням. Для інтервального варіаційного ряду визначається модальний інтервал
де Якщо визначений модальний інтервал, то реалізація такої формули не викликає труднощів. Для строго симетричного розподілу, у якого частоти варіант, які рівновіддалені від моди, рівні, значення середньої арифметичної, медіани і моди співпадають, тобто
На гістограмі розподілу мода визначається таким чином. Знаходиться прямокутник з найбільшою частотою (відносною частотою). З’єднуючи відрізками прямих вершини цього прямокутника з відповідними вершинами двох сусідніх прямокутників, одержують точку перетину цих відрізків (діагоналей), абсциса якої і буде модою варіаційного ряду. Показники варіації Середні величини тим більш характерні для даного розподілу, чим тісніше групуються окремі варіанти навколо середньої, тобто чим менше вони розсіяні. Тому середні характеристики повинні бути доповнені вимірюванням варіації ознаки відносно середньої, тобто характеристиками розсіювання. Сама груба оцінка розсіювання, яка оцінюється за даними варіаційного ряду, може бути одержана за допомогою розмаху варіювання:
де Однак цей показник не дає уявлення про характер варіаційного ряду, розташування варіант навколо середньої і може сильно змінюватись від додавання або виключення крайніх варіант навіть із найменшою частотою. Для оцінки варіювання значень ознаки відносно середньої використовуються різні характеристики розсіювання, які відрізняються одна від одної вибраною формою середнього і способами оцінки відхилень від неї окремих варіант.
Ø Середнім лінійним відхиленнямd варіаційного ряду називається середнє арифметичне абсолютних відхилень значень варіант від їх середньої арифметичної:
Ø Дисперсією
Дисперсія дає характеристику варіації у квадратних одиницях. Для характеристики варіації у тих же одиницях, що і значення ознаки, на базі дисперсії визначається середнє квадратичне відхилення. Ø Середнім квадратичним відхиленнямs називається корінь квадратний із дисперсії:
Характеристикою варіації є також і коефіцієнт варіації, який дорівнює процентному відношенню середнього квадратичного відхилення до середнього арифметичного:
Коефіцієнт варіації має ту ж природу, що і Якщо коефіцієнт варіації ознаки, яка приймає тільки додатні значення, високий (наприклад більше 100%), то як правило, це свідчить про неоднорідність вибірки. Властивості дисперсії: 1. Дисперсія постійної величини дорівнює 0. 2. Якщо усі варіанти збільшити (зменшити) у одне і теж число разів k, то дисперсія збільшиться (зменшиться) у
3. Якщо усі варіанти збільшити (зменшити) на одне і теж число, то дисперсія не зміниться:
4. Дисперсія дорівнює різниці між середнім арифметичним квадратів варіант і квадратом середнього арифметичного:
Дійсно,
5. Якщо варіаційний ряд складається із декількох груп спостережень, то загальна дисперсія дорівнює сумі середнього арифметичного групових дисперсій та міжгрупової дисперсії (правило складання дисперсій):
де
– середнє арифметичне групових дисперсій, m – кількість груп,
– дисперсія j-ї групи,
– міжгрупова дисперсія.
|
|||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 489; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.126.80 (0.033 с.) |
 відповідає її статистична аналогія. Статистичні (вибіркові) числові характеристики є випадковими функціями вибіркових значень.
відповідає її статистична аналогія. Статистичні (вибіркові) числові характеристики є випадковими функціями вибіркових значень. варіаційного ряду називається величина, яка обчислюється на основі вибіркових даних за формулами
варіаційного ряду називається величина, яка обчислюється на основі вибіркових даних за формулами
 – варіанти дискретного варіаційного ряду або середини інтервалів інтервального варіаційного ряду,
– варіанти дискретного варіаційного ряду або середини інтервалів інтервального варіаційного ряду,  – частоти,
– частоти,  – відносні частоти,
– відносні частоти, .
.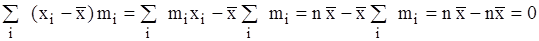 .
. називається величина, яка обчислюється на основі вибіркових даних (для ознак з додатними можливими значеннями) за формулою:
називається величина, яка обчислюється на основі вибіркових даних (для ознак з додатними можливими значеннями) за формулою: (2.6)
(2.6)
 називається величина, яка обчислюється на основі вибіркових даних за формулою:
називається величина, яка обчислюється на основі вибіркових даних за формулою: (2.7)
(2.7) . (2.8)
. (2.8) із умови
із умови  . Значення медіани на цьому інтервалі знаходиться за інтерполяційною формулою:
. Значення медіани на цьому інтервалі знаходиться за інтерполяційною формулою: , (2.9)
, (2.9) – накопичена частота, менша n/2,
– накопичена частота, менша n/2,  – наступна накопичена частота, більша або рівна n/2.
– наступна накопичена частота, більша або рівна n/2. або кумуляти
або кумуляти  як значення варіанти Me, для якої
як значення варіанти Me, для якої 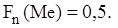 Це зручно зробити графічно.
Це зручно зробити графічно.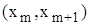 , якому відповідає найбільша щільність відносної частоти. Величина моди всередині модального інтервалу визначається за інтерполяційною формулою
, якому відповідає найбільша щільність відносної частоти. Величина моди всередині модального інтервалу визначається за інтерполяційною формулою , (2.10)
, (2.10) ,
,  ,
,  – частоти відповідно модального, попереднього до модального і наступного за модальним інтервалів. У цій формулі замість частот можна використовувати частки.
– частоти відповідно модального, попереднього до модального і наступного за модальним інтервалів. У цій формулі замість частот можна використовувати частки. . При порушенні симетрії ці три показника розходяться. Але якщо порушення симетрії не дуже сильно виражене, то між вказаними трьома видами середньої буде виконуватись наближена рівність
. При порушенні симетрії ці три показника розходяться. Але якщо порушення симетрії не дуже сильно виражене, то між вказаними трьома видами середньої буде виконуватись наближена рівність . (2.11)
. (2.11) , (2.12)
, (2.12) ,
,  – найменша і найбільша варіанти ряду.
– найменша і найбільша варіанти ряду.
 варіаційного ряду (вибірковою дисперсією) називається середнє арифметичне квадратів відхилень значень варіант від їх середньої арифметичної:
варіаційного ряду (вибірковою дисперсією) називається середнє арифметичне квадратів відхилень значень варіант від їх середньої арифметичної:
 . (2.15)
. (2.15) . (2.16)
. (2.16) , і виявляється більш зручним для порівняльної оцінки варіації у розподілах з різними значеннями середнього арифметичного. Однак він втрачає смисл при
, і виявляється більш зручним для порівняльної оцінки варіації у розподілах з різними значеннями середнього арифметичного. Однак він втрачає смисл при  і стає малонадійним при близьких до 0 значеннях середнього.
і стає малонадійним при близьких до 0 значеннях середнього. разів:
разів:

 .
.
 ,
, – загальна дисперсія, n – об’єм усієї сукупності,
– загальна дисперсія, n – об’єм усієї сукупності,  – загальне середнє;
– загальне середнє;
 – об’єм j-ї групи;
– об’єм j-ї групи;
 -i-та варіанта у j-й групі,
-i-та варіанта у j-й групі, 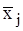 – середнє арифметичне j-ї групи;
– середнє арифметичне j-ї групи;



