
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методи знаходження оцінок параметрів розподілу
Припускається, що невідома функція розподілу належить деякому сімейству розподілів Для побудови оцінок використовуються статистики функції від вибіркових значень. Розповсюдженими статистиками є: · вибіркове середнє · вибіркова дисперсія · вибірковий k-й початковий момент · вибірковий k-й центральний момент Оскільки результати спостережень випадкові, будь-яка статистика представляє собою випадкову величину. Для того, щоб статистика могла служити оцінкою даного параметра Розглянемо основні методи знаходження оцінок. Метод моментів Метод моментів ґрунтується на тому, що невідомі параметри теоретичного розподілу (розподілу генеральної сукупності) визначаються із рівнянь, які дістаються прирівнюванням важливіших числових характеристик (моментів) теоретичного розподілу відповідним числовим характеристикам емпіричного розподілу. Так, нехай заданий, наприклад, вид теоретичного розподілу
і функцію вибірки:
Прирівнюючи їх, одержуємо рівняння для визначення оцінки невідомого параметра
Для знаходження оцінок двох невідомих параметрів
Розв’язуючи цю систему, знаходять відповідні оцінки Оцінки методу моментів звичайно є слушними, однак за ефективністю вони не є «найкращими». Тим не менш, метод моментів часто використовується на практиці, оскільки приводить до порівняно простих обчислень. Приклад 2.2. Знаходження методом моментів оцінки невідомого параметра Статистична модель. Генеральна сукупність має експоненціальний розподіл із щільністю розподілу Розв’язання. Визначимо математичне сподівання експоненціального розподілу:
Далі по вибірці знаходимо вибіркове середнє емпіричного розподілу
Із рівняння
знаходимо оцінку
Алгоритм у Mathсad Початкові дані
Моделювання вибірки об’єму
Фрагмент вибірки
Середнє значення m:= mean(x) m = 0.103 Оцінка параметра
Приклад 2.3. Особливо зручне застосування методу моментів, коли шукані параметри розподілу самі є деякими числовими характеристиками. Знайдемо методом моментів оцінки невідомих параметрів a і Статистична модель. Вибірка
де a і Знайдемо методом моментів оцінки Розв’язання. Визначимо математичне сподівання і дисперсію розподілу:
За даними вибірки знаходимо вибіркові числові характеристики
У результаті одержуємо шукані оцінки параметрів: Алгоритм у Mathсad Початкові дані Моделювання вибірки об’єму
Фрагмент вибірки
Середнє арифметичне і середнє квадратичне
Оцінки параметрів розподілу
|
||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 386; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.73.35 (0.01 с.) |
 , яке залежить від параметра
, яке залежить від параметра 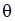 (параметр
(параметр  Так, наприклад, сімейство нормальних розподілів залежить від двох параметрів – математичного сподівання і дисперсії. Потрібно за результатами спостережень (значенням вибірки) оцінити параметр (або декілька параметрів) розподілу.
Так, наприклад, сімейство нормальних розподілів залежить від двох параметрів – математичного сподівання і дисперсії. Потрібно за результатами спостережень (значенням вибірки) оцінити параметр (або декілька параметрів) розподілу. ;
; ;
; ;
; ;
;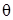 , необхідно, щоб розподіл цієї статистики був зосереджений у достатній близькості від невідомого значення параметра
, необхідно, щоб розподіл цієї статистики був зосереджений у достатній близькості від невідомого значення параметра 

 (2.28)
(2.28) ,
,  звичайно беруть математичне сподівання і дисперсію теоретичного розподілу та відповідні їм числові характеристики емпіричного розподілу – вибіркове середнє
звичайно беруть математичне сподівання і дисперсію теоретичного розподілу та відповідні їм числові характеристики емпіричного розподілу – вибіркове середнє 
 (2.29)
(2.29) .
. експоненціального розподілу.
експоненціального розподілу.
 , де
, де  узяті із однієї і тієї ж генеральної сукупності. Знайдемо методом моментів оцінку
узяті із однієї і тієї ж генеральної сукупності. Знайдемо методом моментів оцінку 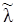 невідомого параметра розподілу
невідомого параметра розподілу 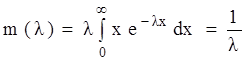 .
. .
.

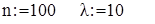
 із генеральної сукупності розподіленої за експоненціальним законом з параметрам
із генеральної сукупності розподіленої за експоненціальним законом з параметрам 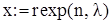
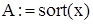

 ◄
◄ нормального розподілу.
нормального розподілу.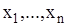 одержана із генеральної сукупності з нормальним розподілом із щільністю розподілу:
одержана із генеральної сукупності з нормальним розподілом із щільністю розподілу: ,
,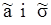 невідомих параметрів a і
невідомих параметрів a і  ,
, 
 і прирівнюємо їх до відповідних числових характеристик теоретичного розподілу:
і прирівнюємо їх до відповідних числових характеристик теоретичного розподілу:

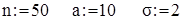
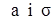 і одержання варіаційного ряду
і одержання варіаційного ряду



 ◄
◄


