
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нахождение точечных оценок закона распределения результатов измеренияСодержание книги
Поиск на нашем сайте
Среднее арифметическое значений из выборки вычисляется по формуле:
где n – число значений в выборке; х i – значение из выборки, мм,
Точечная оценка среднего квадратического отклонения рассчитывается по формуле:
Расчёты числителя дроби, приведённой в формуле (2), сведены в таблицу 5, где к – количество значения по всему объему выборки.
Таблица 5 – Расчет числителя дроби
Окончание таблицы 5
Точечная оценка среднего арифметического значений из выборки вычисляется по формуле:
Производим расчёты по формулам (2) и (3):
Поиск грубых погрешностей Производим поиск грубых погрешностей, используя неравенство:
l хi - где хi – xmax и xmin.
3 × 0,0044 = 0,013. l25,407 – 25,400l = 0,007 (мм). 0,007 < 0,013. l25,392 – 25,400l = 0,008 (мм). 0,008 < 0,013. Вывод: так как наибольшее и наименьшее значения выборки меньше 3 × Sx, следовательно, они не являются грубыми погрешностями и не отбрасываются.
Определение закона распределения результатов измерений и их случайных погрешностей Строим вариационный ряд, располагая все результаты в порядке возрастания от y1(min xi) до yn(max xi).
25,392 мм 25,400 мм 25,403 мм 25,392 мм 25,400 мм 25,403 мм 25,392 мм 25,400 мм 25,403 мм 25,394 мм 25,400 мм 25,403 мм 25,394 мм 25,401 мм 25,404 мм 25,396 мм 25,401 мм 25,404 мм 25,397 мм 25,401 мм 25,407 мм 25,399 мм 25,401 мм 25,407 мм 25,399 мм 25,402 мм 25,407 мм 25,400 мм 25,402 мм 25,407 мм
Данный ряд разбиваем на оптимальное число одинаковых интервалов группирования. Длину интервалов группирования рассчитываем по формуле:
где m – число интервалов группирования. За m принимается целое нечётное число в пределах от mmin до mmax, которые рассчитываются по формулам (6) и (7), соответственно:
(6)
(7) таким образом, принимаем m = 3. Определяем длину интервалов по формуле (5):
Определяем интервалы группирования данных в виде:
Подсчитываем число попаданий результатов измерений,nkn в каждый интервал: nk1=7, nk2=13, nk3=10. Рассчитываем вероятность попадания, Рк, результатов измерения в каждый из интервалов группирования по формуле:
где n – сумма попаданий во все интервалы.
Проведённые расчёты позволяют построить гистограмму и полигон, для этого по оси результатов х, откладываем интервалы в порядке возрастания номеров и на каждом интервале строим прямоугольник высотой Рк. Полигон представляет собой ломаную кривую, соединяющую середину верхних оснований каждого столбца диаграммы. За пределами гистограммы остаются пустые интервалы, в которых точки, соответствующие их серединам лежат на оси. Эти точки при построении полигона соединяем отрезками прямых линий. Полигон более точно отражает форму кривой распределения (рисунок 10).
Рисунок 10
Вывод: результаты измерений и их погрешности распределены по нормальному закону.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 218; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.1.23 (0.009 с.) |

 (1)
(1) - среднее арифметическое значений из выборки, мм.
- среднее арифметическое значений из выборки, мм. (мм).
(мм). (2)
(2) (3)
(3) ;
; (5)
(5)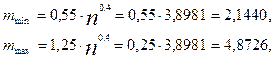

 . (8)
. (8)
 (9)
(9)




