
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Підалгебри Картана і розклад по кореневим підпросторамСодержание книги
Поиск на нашем сайте
Нехай 𝐿 – алгебра Лі над 𝑃. Підалгебра 𝐻 в 𝐿 називається підалгеброю Картана, якщо вона нільпотентна і співпадає зі своїм нормалізатором в 𝐿. (Нормалізатор алгебри 𝐻 – це {𝑋 ∈ 𝐿: [𝑋, 𝐻] ⊂ 𝐻}). Нехай тепер 𝑃= Так як підалгебра 𝐻 нільпотентна, то для кожного 𝑋 ∈ 𝐻 узагальнений власний підпростір, що відповідає власному значенню 0, містить 𝐻. Звідси, ми можемо вважати, що 𝛼0 ≡ 0 і 𝐿 (𝛼0) = 𝐿 (0) = {𝑌 ∈ 𝐿: для довільного 𝑋 ∈ 𝐻 існує ціле число 𝑒 ≥ 1, таке що (𝑎𝑑 𝑋)𝑒𝑌 = 0}. Якщо 𝐻 ≠ 𝐿 (0), то існує елемент 𝑠0 ∈ 𝐿 (0), що 𝑠0 ∉ 𝐻 і [𝐻, 𝑠0] ⊂ 𝐻. Але в такому випадку 𝑠0 належить нормалізатору підалгебри 𝐻, що співпадає за припущенням з 𝐻, - суперечність. Значить, 𝐻 = 𝐿 (0). Далі, [𝐿 (𝛼𝑖), 𝐿 (𝛼𝑗)] міститься в узагальненому власному під-просторі ендоморфізма 𝑎𝑑 𝑋, що відповідає власному значенню 𝛼𝑖(𝑋)+𝛼𝑗(𝑌), для довільного 𝑋 ∈ 𝐻. Так як 𝐿 (𝛼𝑖 + 𝛼𝑗) представляє собою перетин всіх таких підпросторів, то [𝐿 (𝛼𝑖), 𝐿 (𝛼𝑗)] ⊂ 𝐿 (𝛼𝑖 + 𝛼𝑗). Функції 𝛼1, …, 𝛼𝑘 називаються коренями, а розклад 𝐿 = 𝐻 ⨁ 𝐿 (𝛼1) ⨁ … ⨁ 𝐿 (𝛼𝑘) - розклад по кореневим підпросторам алгебри 𝐿 відносно 𝐻.
Напівпрості алгебри Лі Нехай 𝐿 – алгебра Лі над 𝑃 = (1) 𝐿 = 𝐿 (0) ⨁ 𝐿 (𝛼1) ⨁ … ⨁ 𝐿 (𝛼𝑘) - її розклад на кореневі підпростори відносно підалгебри Картана 𝐿(0)=𝐿0. Нехай 𝑉 – векторний простір над 𝑃 і (𝑉, 𝑓) – представлення алгебри 𝐿. Так як відображення 𝐿0 ∋ 𝑋 ↦ 𝑓 (𝑋) ∈ 𝑔𝑙 (𝑉) є представленням нільпотентної алгебри Лі, то ми отримуємо розклад підпростору 𝑉 в пряму суму
(2) 𝑉 = 𝑉 (𝜆1) ⨁ 𝑉(𝜆2) ⨁ …, де 𝜆𝑖 (𝑖 = 1, 2, …) - функції із 𝐿0 в 𝑃 і для довільного 𝑋 ∈ 𝐿0 підпростір 𝑉 (𝜆𝑖) міститься в узагальненому власному підпросторі ендоморфізма 𝑓(𝑋), що відповідає власному значенню 𝜆𝑖 (𝑋). Функції 𝛼1, 𝛼2, …, 𝜆1, …, лінійні; функції 𝜆𝑖 називаються вагами алгебри 𝐿 відносно підалгебри Картана 𝐿0 (і представлення (𝑉, 𝑓)). Розуміється, функції 𝛼1, …, 𝛼𝑘 можна вважати попарно різними, тому існує такий елемент 𝑋 ∈ 𝐿0, що всі числа 𝛼𝑖 (𝑋) відмінні від нуля і від один одного. При такому виборі 𝑋 підпростори 𝐿(𝛼𝑖) співпадають з узагальненими власними підпросторами ендоморфізма 𝑎𝑑 𝑋, що відповідають власним значенням 𝛼𝑖 (𝑋). Звідси, [𝐿 (𝛼𝑖), 𝐿 (𝛼𝑗)] міститься в власному підпросторі, що відповідає власному значенню 𝛼𝑖 (𝑋) + 𝛼𝑗 (𝑋)тобто в 𝐿 (𝛼𝑖 + 𝛼𝑗). Таким чином (3) [𝐿 (𝛼), 𝐿 (𝛽)] ⊂ 𝐿 (𝛼 + 𝛽), де 𝛼, 𝛽 - корені (або 0). Аналогічні міркування дають (4) 𝐿 (𝛼) 𝑉 (𝜆) ⊂ 𝑉 (𝛼 + 𝜆). В (3) і (4) як і раніше мається на увазі, що 𝐿 (𝛼 + 𝛽) = 0, якщо 𝛼 + 𝛽 (≠ 0) не є коренем, і 𝑉 (𝛼 + 𝜆) = 0, якщо 𝛼 + 𝜆 не є вагою. Теорема 2. 3. 1. Нехай 𝐿 – напівпроста алгебра Лі над 𝑃. 1) 𝐿 розкладається в пряму суму простих ідеалів, причому цей розклад однозначний з точністю до порядку доданків. 2) Ідеали і факторалгебри алгебри 𝐿 напівпрості. 3) 𝐿 = 𝐿(1) 4) Алгебра 𝐿 – повна. 5) Для довільного розширення Нехай 𝐿 – алгебра Лі. Довільна підалгебра 𝐴 в 𝐿, інваріантна відносно всіх диференціювань алгебри 𝐿: 𝑑𝑒𝑟(𝐿) 𝐴 ⊂ 𝐴, називається характеристичною. Характеристичні підалгебри є ідеалами. Для довільних 𝑋, 𝑌 ∈ 𝐿 і 𝛿 ∈ 𝑑𝑒𝑟 (𝐿) 𝛿 [𝑋, 𝑌] = [𝛿𝑋, 𝑌] + [𝑋, 𝛿𝑌], і тому 𝐿(1) – характеристична підалгебра. Твердження 2. 3. 2. Радикал є характеристичною підалгеброю.
|
||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 376; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.163.15 (0.009 с.) |

 і 𝐿 – алгебра Лі над 𝑃. Припустимо, що в 𝐿 існує під- алгебра Картана. Існують різні функції 𝛼0, 𝛼1, …, 𝛼𝑘 із 𝐻 в 𝑃 і підпростору 𝐿 (𝛼0), 𝐿 (𝛼1), …, 𝐿 (𝛼𝑘) в 𝐿 такі, що 𝐿 = 𝐿 (𝛼0) ⨁ … ⨁ 𝐿 (𝛼𝑘), 𝐿 (𝛼) = {𝑌 ∈ 𝐿: для довільного 𝑋 ∈ 𝐻 існує ціле число 𝑒 ≥ 1, таке що (𝑎𝑑 𝑋 − 𝛼𝑖 (𝑋))𝑒𝑌= 0}.
і 𝐿 – алгебра Лі над 𝑃. Припустимо, що в 𝐿 існує під- алгебра Картана. Існують різні функції 𝛼0, 𝛼1, …, 𝛼𝑘 із 𝐻 в 𝑃 і підпростору 𝐿 (𝛼0), 𝐿 (𝛼1), …, 𝐿 (𝛼𝑘) в 𝐿 такі, що 𝐿 = 𝐿 (𝛼0) ⨁ … ⨁ 𝐿 (𝛼𝑘), 𝐿 (𝛼) = {𝑌 ∈ 𝐿: для довільного 𝑋 ∈ 𝐻 існує ціле число 𝑒 ≥ 1, таке що (𝑎𝑑 𝑋 − 𝛼𝑖 (𝑋))𝑒𝑌= 0}. , і нехай
, і нехай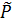 поля 𝑃 алгебра
поля 𝑃 алгебра  напівпроста.
напівпроста.


