
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ідеали, розв’язність, нільпотентність.
Нехай 𝕭1 і 𝕭2 – підпростори алгебри Лі 𝕷. Позначимо через 𝕭1 ⋂ 𝕭2 перетин цих підпросторів, а через 𝕭1 + 𝕭2 – підпростір, натягнутий над 𝕭1 і 𝕭2. Підпростір 𝕭1 + 𝕭2 є сукупністю елементів виду 𝑏1 + 𝑏2, де 𝑏і ⋲ 𝕭і. Визначимо тепер [𝕭1 𝕭2] як підпростір, натягнутий на всі добутки [𝑏1 𝑏2], 𝑏і ⋲ 𝕭і. Звідси зразу випливає, що елементами простору [𝕭1 𝕭2] є суми 1. [𝕭1 𝕭2] = −[𝕭2 𝕭1]. 2. [𝕭1 + 𝕭2, 𝕭3] = [𝕭1 𝕭3] + [𝕭2 𝕭3]. 3. [[𝕭1 𝕭2] 𝕭3] ⊆ [[𝕭1 𝕭3] 𝕭2] + [[𝕭2 𝕭3]𝕭1]. (3) 4. [𝕭1 ⋂ 𝕭2,𝕭3] ⊆ [𝕭1 𝕭3] ⋂ [𝕭2 𝕭3]. Підпростір 𝕭 є ідеалом тоді і тільки тоді, коли [𝕭𝕷] ⊆ 𝕭. Перетин та сума ідеалів утворюють ідеал, а властивість 3, якщо положити 𝕭3 = 𝕷, показує, що це справедливо і для (лієвого) добутку ідеалів. Зокрема, очевидно, що члени похідного ряду 𝕷 ⊇ 𝕷’ = [𝕷𝕷] ⊇ ⊇ 𝕷’’ = [𝕷𝕷] ⊇… ⊇ 𝕷k = [𝕷(k-1)𝕷(k-1)] ⊇… є ідеалами. Це ж саме вірно і для членів нижнього центрального ряду 𝕷 ⊇ 𝕷2 = 𝕷’ ⊇ ⊇ 𝕷3 = [𝕷2𝕷] ⊇… ⊇ 𝕷k = [𝕷k-1𝕷] ⊇… Алгебра Лі називається розв’язною, якщо 𝕷(h) = 0 для деякого додатного числа 𝗁. Кожна абелева алгебра розв’язна. Для опису алгебр Лі розмірностей, не більших 3, випливає, що всі ці алгебри розв’язні, за виключенням тих, для яких dim𝕷 = 3 = dim𝕷’. Лема 1. 3. 1. Довільна підалгебра і довільний гомоморфний образ розв’язної алгебри Лі розв’язні. Якщо 𝕷 містить розв’язний ідеал 𝕭, такий що факторалгебра 𝕷/𝕭 розв’язна, то і сама алгебра 𝕷 розв’язна. Твердження 1. 3. 2. Сума довільних двох розв’язних ідеалів є роз-в’язним ідеалом. Припустимо тепер, що алгебра 𝕷 має скінченну розмірність, і нехай 𝕾 – розв'язний ідеал максимальної розмірності в 𝕷. Тоді із останнього твердження випливає, що якщо 𝕭 – довільний розв'язний ідеал в 𝕷, то 𝕾 + 𝕭 – також розв’язний ідеал. Але 𝕾 + 𝕭 = 𝕾, оскільки розмірність ідеалу 𝕾 максимальна за припущенням. Звідси, 𝕾 ⊇ 𝕭. Цим доведено існування розв'язного ідеалу 𝕾, що містить довільний інший розв'язний ідеал. Ми назвемо 𝕾 радикалом алгебри 𝕷. Якщо 𝕾 = 0, тобто якщо алгебра 𝕷 не має розв'язних ідеалів, відмінних від 0, то алгебра 𝕷 називається напівпростою. Якщо 𝕷 немає ідеалів взагалі, відмінних від 0 і 𝕷, і якщо 𝕷’≠0, то алгебра 𝕷 називається простою. Якщо 𝕷 проста, а 𝕾 – її радикал, то або 𝕷 = 𝕾, або 𝕾 = 0. Але якщо 𝕷 = 𝕾, то 𝕾’ ⊂ 𝕾 і 𝕾’ – ідеал, так що 𝕾’=𝕷’= 0, що суперечить означенню. Тому 𝕾 = 0, тобто з умови простоти випливає напівпростота. Якщо 𝕾 – радикал, то довільний розв'язний ідеал в 𝕷/𝕾 має вигляд 𝕭/𝕾, де 𝕭 – ідеал в 𝕷. Але ідеал 𝕭 розв'язний по лемі; тому 𝕭 ⊆ 𝕾 і 𝕭/𝕾 = 0. Таким чином алгебра 𝕷/𝕾 – напівпроста. Якщо 𝕭 – ненульовий розв'язний ідеал в 𝕷 і 𝕭(h-1) ≠ 0, 𝕭(h) = 0, то 𝕭(h-1) абелевий ідеал в 𝕷, відмінний від нуля. Тому алгебра 𝕷 напівпроста, якщо в ній немає ненульових абелевих ідеалів. Трьохвимірні алгебри Лі, для яких dim 𝕷’ = 3 (або 𝕷’ = 𝕷) прості.
Алгебра Лі 𝕷 називається нільпотентною, якщо 𝕷k = 0 для деякого додатного числа k. Тепер як і в випадку розв'язних ідеалів, можна зробити висновок, що в скінченновимірній алгебрі Лі 𝕷 існує нільпотентний ідеал 𝕽 що містить кожен нільпотентний ідеал із 𝕷. Ми назвемо 𝕽 ніль-радикалом алгебри 𝕷. Він міститься в радикалі 𝕾. В випадку двохвимірної неабелевої алгебри 𝜱𝘦 + 𝜱𝘧, [𝘦𝘧] = 𝘦, 𝕾 = 𝕷 і 𝕽 = 𝜱𝘦. Факторалгебра 𝕷/𝕽 абелева і тому нільпотентна. Таким чином, можливе строге включення 𝕾 ⊃ 𝕽, і 𝕷/𝕽 може мати ненульовий ніль-радикал. Теорія нільпотентних радикалів і ідеалів має аналог у випадку асоціативних алгебр. Якщо 𝕭1 і 𝕭2 – підпростори асоціативної алгебри 𝕬, то через 𝕭1𝕭2 позначається підпростір, натягнутий на всі добутки 𝑏1𝑏2, 𝑏і⋲ 𝕭і. Алгебра 𝕬 називається нільпотентною, якщо існує таке додатнє число 𝑘, що 𝕬𝑘 =0 (𝕬1 = 𝕬, 𝕬𝑘 = 𝕬𝑘-1𝕬). Це еквівалентне тому, що кожен добуток 𝑘 елементів із 𝕬 рівний 0. Якщо 𝕽1 і 𝕽2 – нільпотентні ідеали в 𝕬, то, як легко довести, 𝕽1 + 𝕽2 – також нільпотентний ідеал. Тому, якщо алгебра 𝕬 – скінченновимірна, то в 𝕬 існує максимальний нільпотентний ідеал 𝕽, що містить кожен нільпотентний ідеал. Ідеал 𝕽 називається радикалом алгебри 𝕬. Алгебра 𝕬/𝕽 напівпроста в тому сенсі, що вона немає нільпотентних іделів, відмінних від нуля.
Приклади 1. Довестипершу та другувластивості закону композиції [𝕭1𝕭2] (3). Доведення: 1. [𝕭1 𝕭2] = 2. [𝕭1 + 𝕭2, 𝕭3] = = 2. Нехай 𝕬, 𝕭 – асоціативні алгебри. Показати, що якщо 𝛉 –гомоморфізм алгебри 𝕬 в 𝕭, то 𝛉 є гомоморфізмом алгебри 𝕬𝐿 в 𝕭𝐿. Доведення: 𝛉 – гомоморфізм алгебри 𝕬 в 𝕭 ⟹ для операцій «−» та «×», визначених на даних алгебрах для ∀ 𝑎1 ∈ 𝕬, 𝑏1 ∈ 𝕭 виконується: 𝛉 (𝑎1 − 𝑏1) = 𝛉 (𝑎1) – 𝛉 (𝑏1); 𝛉(𝑎1 × 𝑏1 ) = 𝛉 (𝑎1) × 𝛉(𝑏1) ⟹ ∀ 𝑎2 ∈ 𝕬𝐿, 𝑏2 ∈ 𝕭𝐿 𝛉 ([𝑎2 𝑏2]) = 𝛉 (𝑎2𝑏2 − 𝑏2𝑎2) = 𝛉 (𝑎2𝑏2) – 𝛉 (𝑏2𝑎2) = 𝛉 (𝑎2) × 𝛉 (𝑏2) − 𝛉(𝑏2) × ×𝛉 (𝑎2) =[ 𝛉 (𝑎2) 𝛉 (𝑏2)] ∎ 3. Якщо 𝑆 – підмножина в лієвій алгебрі 𝕷, то централізатором 𝕮(𝑆) є підмножина таких елементів 𝑐, що [𝑠𝑐]=0 для всіх 𝑠 ∈ 𝑆. Показати, що 𝕮(𝑆) – підалгебра. Доведення: включення очевидне, доведемо замкненість. ∀ 𝑐 ∈ 𝕮(𝑆) [𝑠𝑐] = 𝑠𝑐 − 𝑐𝑠 = 0 ⟹ 𝑠𝑐 = 𝑐𝑠 ⟹ ∀ 𝑐1, 𝑐2 ∈ 𝕮(𝑆) [𝑠,𝑐1𝑐2] = 𝑠𝑐1𝑐2 − 𝑐1𝑐2𝑠 = = 𝑐1𝑠𝑐2− 𝑐1𝑐2𝑠 = 𝑐1𝑐2𝑠 − 𝑐1𝑐2𝑠 = 0. ∎ 4. Перевірити, що якщо 𝕷 має базис (е1, е2, …, е8) з таблицею множення [𝑒1 𝑒2] = 𝑒5, [𝑒1 𝑒3] = 𝑒6, [𝑒1 𝑒4] = 𝑒7, [𝑒1 𝑒5] = −𝑒8, [𝑒2 𝑒3] = 𝑒8, [𝑒2 𝑒4] = 𝑒6, [𝑒2 𝑒6] = −𝑒7, [𝑒3 𝑒4] = −𝑒5, [𝑒3 𝑒5] = −𝑒7, [𝑒4 𝑒6] = −𝑒8, всі решта [𝑒𝑖 𝑒𝑗] = 0, і для 𝑖 < 𝑗 [𝑒𝑖 𝑒𝑖] = 0, [𝑒𝑖 𝑒𝑗] = −[𝑒𝑗 𝑒𝑖], то 𝕷 – нільпотентна алгебра Лі. Доведення: Нехай (α,𝑒): = α1𝑒1 + α2𝑒2 + … + α8𝑒8 ∈ 𝕷, де α – деякий скаляр. При піднесенні даного елемента до квадрату ми отримаємо елемент виду β5𝑒5 + β6𝑒6 + β7𝑒7 + β8𝑒8. Знову підносимо до квадрату, в результаті чого отримуємо 0. Отже, дана алгебра Лі 𝕷 є нільпотентною з ступенем нільпотентності 3. ∎
Розділ 2 Напівпрості алгебри Лі Наша перша ціль – показати, що алгебра Лі над полем характеристики 0 напівпроста тоді і тільки тоді, коли вона не вироджена. З огляду на теорему 2. 1. 2., можна звести вивчення напівпростих алгебр Лі до вивчення простих алгебр Лі. На протязі всього цього розділу вважається, що основне поле Р має характеристику 0.
|
||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 321; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.63.145 (0.011 с.) |
 𝑏іj ⋲ 𝕭і. Сформулюємо основні властивості закону композиції [𝕭1 𝕭2]:
𝑏іj ⋲ 𝕭і. Сформулюємо основні властивості закону композиції [𝕭1 𝕭2]: =
= 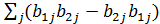 = −
= −  = −[𝕭2 𝕭1].
= −[𝕭2 𝕭1]. =
=  =
=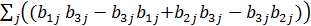 = [𝕭1 𝕭3] + [𝕭2 𝕭3].
= [𝕭1 𝕭3] + [𝕭2 𝕭3].


