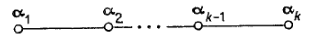Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розклад по кореневим підпросторам
Нехай 𝑔 – напівпроста алгебра Лі над 𝑃 = Твердження 2. 4. 1. Якщо 𝛽 ∈ Введемо в 𝔥 скалярний добуток по формулі <𝑋, 𝑌> = 𝐵 (𝑋, 𝑌) = Оскільки форма 𝐵𝔥 не вироджена, то для кожного 𝜆 ∈ 𝔥* існує єдиний елемент 𝐻𝜆 ∈ 𝔥, такий що 𝜆 (𝐻) = <𝐻𝜆, 𝐻> при всіх 𝐻 ∈ 𝔥. Це дозволяє визначити невироджений, скалярний добуток в 𝔥* формулою <𝜆, 𝜇> = <𝐻𝜆, 𝐻𝜇> = 𝜆 (𝐻𝜇) = 𝜇 (𝐻𝜆) (𝜆, 𝜇 ∈ 𝔥*). Теорема 2. 4. 2. В кожному із (одновимірних) підпросторів 𝑔 (𝛼), 𝛼 ∈ 𝛥, можна вибрати базисний вектор 𝐸𝛼 так, що 𝑔 = 𝔥 + 𝑃𝐸𝛼 + 𝑃𝐸-𝛼 + 𝑃𝐸 𝛽 + 𝑃𝐸-𝛽 +…, Причому виконуються наступні умови: 1) підалгебра 𝔥 абелева і [𝐻, 𝐸𝛼] = 𝛼 (𝐻) 𝐸𝛼 (𝛼 ∈ 𝛥) при 𝐻 ∈ 𝔥; зокрема, 𝑎𝑑 𝐻 є напівпростим лінійним перетворенням; 2) [𝐸𝛼, 𝐸𝛽] = 𝑁𝛼, 𝛽 𝐸𝛼 + 𝛽 (𝑁𝛼, 𝛽 ∈ 𝑃) при 𝛼 + 𝛽 ≠ 0; 3) [𝐸𝛼, 𝐸-𝛼] = − 𝐻𝛼 і 𝐵 (𝐸𝛼, 𝐸-𝛼) = − 1 (знак мінус перед 𝐻𝛼 виявиться зручним в подальшому); 4) якщо 𝛼 ∈ 𝛥 і 𝑘𝛼 ∈ 𝛥 (𝑘 ∈ ℤ), то 𝑘 = ± 1; 5) 𝐵 (𝐻 + (𝐵 (𝐻, 𝐻′) = <𝐻, 𝐻′> = 6) для довільних 𝜆, 𝜇 ∈ 𝔥* <𝜆, 𝜇> =
2. 5. 𝛼 – послідовність ваг Нехай (𝑉, 𝑓) - представлення алгебри 𝑔. Позначимо через 𝛬 сукупність всіх ваг відносно (𝑉, 𝑓). Це – скінченна підмножина в 𝔥*. Твердження 2. 5. 1. Для довільних заданих 𝛼 ∈ 𝛥 і 𝜆 ∈ 𝛬 можна знайти такі невід’ємні цілі числа 𝑗 і 𝑘, що 1) 𝜆 + 𝑖𝛼 ∈ 𝛬 (𝑖 ∈ ℤ) тоді і тільки тоді, коли –𝑗 ≤ 𝑖 ≤ 𝑘;
2) 𝑘 – 𝑗 = −2 <𝜆, 𝛼>/<𝛼, 𝛼>; 3) 𝜆 – (2 <𝜆, 𝛼>/<𝛼, 𝛼>), 𝛼 ∈ 𝛬; 4) якщо 𝜆 + 𝛼 ∈ 𝛬, то 𝐸𝛼𝑉 (𝜆) ≠ 0. Означення 2. 5. 2. Послідовність 𝜆 – 𝑗𝛼, 𝜆 – (𝑗 − 1)𝛼, …, 𝜆, …, 𝜆 + 𝑘𝛼 із попереднього твердження будемо називати 𝛼 – послідовністю (ваг), що містить 𝜆. Твердження 2. 5. 3. 1) Якщо 𝛼, 𝛽 і 𝛼 + 𝛽 ∈ 𝛥, то 𝑁𝛼, 𝛽 ≠ 0. 2) Якщо 𝛼 ∈ 𝛬 і 𝑚𝛼 ∈ 𝛥 (𝑚 ∈ 𝑃), то 𝑚 = ±1.
2. 6. Фундаментальна система коренів і 𝜋 – система. Нехай Покладемо 𝛥+ = {𝛼 ∈ 𝛥: 𝛼 > 0} і 𝛥− = {𝛼 ∈ 𝛥: 𝛼 < 0} = {−𝛼: 𝛼 ∈ 𝛥+}. Ясно, що 𝛥 = 𝛥+ ∪ 𝛥− і 𝛥+ ∩ 𝛥− = ∅. Означення 2. 6. 1. Корінь 𝛼 із 𝛥+ називається простим, якщо його не можна записати у вигляді 𝛼 = 𝛽 + 𝛾, де 𝛽 ∈ 𝛥+, 𝛾 ∈ 𝛥+. (Наприклад, найменший додатній корінь простий.) Підмножина 𝐺 в
Для 𝜆 ∈ Означення 2. 6. 2. В просторі ℝ𝑙 зі скалярним добутком <(𝑥1, …, 𝑥𝑙), (𝑦1, …, 𝑦𝑙)> = підмножина 𝐷 називається кореневою системою, якщо 1) для довільного 𝛼 ∈ 𝐷 ми маємо: 𝛼 ≠ 0 і ℝ𝛼 ∩ 𝐷 = {±𝛼}; 2) для довільних 𝛼, 𝛽 ∈ 𝐷 ми маємо: 2 <𝛽, 𝛼>/<𝛼, 𝛼> ∈ ℤ і 𝛽 – 𝑘𝛼 ∈ 𝐷 для всіх цілих чисел 𝑘, що містяться між 0 і 2 <𝛽, 𝛼>/<𝛼, 𝛼>. В випадку, якщо не сказано іншого, ми вважаємо, що 𝐷 породжує ℝ𝑙. Ототожнимо Твердження 2. 6. 3. Позначимо через 𝜋 сукупність всіх простих коренів із 𝛥 (відносно деякого фіксованого упорядкування) 1) 𝜋 = {𝛼1, 𝛼2, …, 𝛼𝑙}утворює базис в 2) Якщо 𝛽 ∈ 𝛥+, то (*) 𝛽 = 𝑛1𝛼1 + … + 𝑛𝑙𝛼𝑙, де 𝑛𝑖 ∈ ℤ, 𝑛𝑖 ≥ 0 при 𝑖 = 1, 2, …, 𝑙. Означення 2. 6. 4. Підмножина 𝜋 множини 𝛥 називається фундаментальною системою коренів, якщо 1) 𝜋 = {𝛼1, 𝛼2, …, 𝛼𝑙}утворює базис в 2) довільне 𝛽 ∈ 𝛥 можна представити у вигляді 𝛽 = 𝑛1𝛼1 + … + 𝑛𝑙𝛼𝑙 (𝑛𝑖 ∈ ℤ), де всі 𝑛𝑖 ≥ 0 або всі 𝑛𝑖 ≤ 0. Означення 2. 6. 5. Введемо в ℝ𝑙 звичайний скалярний добуток <(𝑥1, …, 𝑥𝑙), (𝑦1, …, 𝑦𝑙)> = Підмножина 𝜋 = {𝛼1, 𝛼2, …, 𝛼𝑙}простору ℝ𝑙 називається 𝜋-системою, якщо 1) набір {𝛼1, 𝛼2, …, 𝛼𝑙}лінійно-незалежний; 2) 𝑐𝑖𝑗 = − 2 <𝛼𝑖, 𝛼𝑗>/<𝛼𝑗, 𝛼𝑗> ∈ ℤ при 𝑖, 𝑗 = 1, 2, …, 𝑙, причому 𝑐𝑖𝑗 ≥ 0, якщо 𝑖 ≠ 𝑗. Будемо називати 𝑐𝑖𝑗 числами Картана, а матрицю (𝑐𝑖𝑗) - матрицею Картана. Будь-яку фундаментальну систему коренів 𝜋 можна розглядати як 𝜋-систему. Твердження 2. 6. 6. Фундаментальна система коренів 𝜋 нероз-кладна тоді і тільки тоді, коли алгебра 𝑔 проста. 2. 7. Класифікація 𝜋 – систем Дві 𝜋 – системи 𝜋 = {𝛼1, …, 𝛼𝑙}і Нехай 𝜋 = {𝛼1, …, 𝛼𝑙} - деяка 𝜋 – система. Використовуючи позначення cos 𝛼𝛽 = cos ∠ (𝛼, 𝛽), ми маємо при 𝑖 ≠ 𝑗 𝑐𝑖𝑗𝑐𝑗𝑖 =
Так як |cos 𝛼𝑖𝛼𝑗| < 1, то 𝑐𝑖𝑗c𝑗𝑖 = 0, 1, 2, 3. Припустимо, що ∥𝛼𝑖∥ ≥ ∥𝛼𝑗∥. Випадок 1. 𝑐𝑖𝑗c𝑗𝑖 = 1. Тоді 𝑐𝑖𝑗 = c𝑗𝑖 = 1 тобто Звідси, ∥𝛼𝑖∥ = ∥𝛼𝑗∥. Із рівності 4 cos2𝛼𝑖𝛼𝑗 = 1 ми отримуємо, що ∠( Випадок 2. 𝑐𝑖𝑗 c𝑗𝑖 = 2. Аналогічно попередньому ми маємо 𝑐𝑖𝑗 = 2, c𝑗𝑖 = 1, а тому ∥𝛼𝑖∥2 = 2 ∥𝛼𝑗∥2 і ∠ ( Випадок 3. 𝑐𝑖𝑗c𝑗𝑖 = 3. Маємо 𝑐𝑖𝑗 = 3, c𝑗𝑖 = 1, тому ∥𝛼𝑖∥2 = 3 ∥𝛼𝑗∥2 і ∠ ( Випадок 0. 𝑐𝑖𝑗c𝑗𝑖 = 0. Тоді ∠ ( Діаграма Динкіна. 𝐷 (𝜋) системи 𝜋 складається із 𝑙 вершин (що зображаються у вигляді маленьких кружків), по одній на кожне 𝛼𝑖 ∈ 𝜋,і деякої множини відрізків, що з’єднують ці вершини. Ми проводимо 0, 1, 2 або 3 лінії від 𝛼𝑖 до 𝛼𝑗. Таким чином, перерахованим вище випадкам відповідають діаграми 0) 𝛼𝑖 𝛼𝑗 1) 𝛼𝑖 𝛼𝑗 2) 𝛼𝑖 𝛼𝑗 3) 𝛼𝑖 𝛼𝑗 o o o o o o o o Кажуть, що два елемента 𝛼, 𝛽 системи 𝜋 зв’язані між собою, якщо <𝛼, 𝛽> ≠ 0. Підмножина 𝐷1 в 𝐷 (𝜋) називається зв’язною, якщо для довільних 𝛼, 𝛽 ∈ 𝐷1 знайдеться послідовність 𝛼 = 𝛾0, 𝛾1, …, 𝛾𝑘 = 𝛽 в 𝐷1, така, що елементи 𝛾𝑖, 𝛾𝑖 + 1 зв’язані між собою для 𝑖 = 0, …, 𝑘 – 1. Ясно, що діаграма 𝐷 (𝜋) зв’язна тоді і тільки тоді, коли система 𝜋 нерозкладна. Дальше, якщо діаграми 𝐷 (𝜋) і 𝐷 ( Твердження 2. 7. 1. Для довільної 𝜋 – системи 𝜋 = {𝛼1, …, 𝛼𝑙} число пар вершин, зв’язаних одна з одною, не перевищує 𝑙 – 1. Зауважимо, що кожну підмножину 𝜋 – системи можна розглядати як 𝜋 – систему. Твердження 2. 7. 2. Нехай 𝜋 = {𝛼1, …, 𝛼𝑙} - деяка 𝜋 – система. 1) 𝐷 (𝜋) не має циклів, тобто підмножин {𝛼1, …, 𝛼𝑘}таких що <𝛼1, 𝛼2> ≠ 0, …, <𝛼𝑘 – 1, 𝛼𝑘> ≠ 0 і <𝛼𝑘, 𝛼1> ≠ 0.
2) Нехай 𝐷1 - зв’язна підмножина в 𝐷 (𝜋). Якщо 𝛼 ∈ 𝐷 (𝜋) і 𝛼 ∉ 𝐷1, то існує не більше одного 𝛽 ∈ 𝐷1, зв’язаного з 𝛼. 3) Через кожну вершину проходить не більше трьох відрізків. 4) Якщо 𝜋 нерозкладна і 𝑙 ≥ 3, то 𝐷 (𝜋) не містить підмножин виду o o. Нехай 𝜋 = {𝛼1, …, 𝛼𝑙} - деяка 𝜋-система. Підмножина 𝐶 = {𝛼1, …, 𝛼𝑘} називається однорідним ланцюгом, якщо 𝑐𝑖, 𝑖 + 1 = 𝑐𝑖 +1, 𝑖 = 1 при 𝑖 = 1, 2, …, 𝑘 – 1, тобто відповідна частина діаграми системи має вигляд Твердження 2. 7. 3. Нехай в 𝜋 – системі 𝜋 = {𝛼1, …, 𝛼𝑘, 𝛽1, …, 𝛽𝑗} підмножина 𝐶 = {𝛼, …, 𝛼𝑘} є однорідним ланцюгом. Тоді фактор система 𝜋∕𝐶 = {𝛼, 𝛽1, …, 𝛽𝑗}, де 𝛼 = 𝛼1 + … + 𝛼𝑘, також є 𝜋 – системою. Діаграма 𝐷 (𝜋∕𝐶) виходить наступним чином. Між вершинами 𝛽s і 𝛽𝑡 проводяться ті ж відрізки, що й в 𝐷 (𝜋). Кожна вершина 𝛽s з’єднана в 𝐷 (𝜋) не більш чим з одною із вершин 𝛼; якщо 𝛽s не з’єднана в 𝐷 (𝜋) ні з одною із 𝛼𝑖, то ми не з’єднуємо 𝛽s, з 𝛼, а якщо 𝛽s з’єднана з 𝛼𝑖, то з’єднуємо її з 𝛼 точно так, як вона була з’єднана з 𝛼𝑖 в 𝐷(𝜋). Теорема 2. 7. 4. Нехай 𝜋 – нерозкладна 𝜋 – система. Тоді діаграма Динкіна 𝐷 (𝜋) співпадає з однією із наступних діаграм: 𝐴𝑙 o o … o o 𝑙 ≥ 1 𝐵𝑙 o o … o o 𝑙 ≥ 2 𝐶𝑙 o o … o o 𝑙 ≥ 3 o 𝐷𝑙 o o … o o 𝑙 ≥ 4 o 𝐸𝑙 o o … o o o 𝑙 = 6, 7, 8 𝐹4 o o o o 𝐺2 o o Знайдемо 𝜋 – системи, що відповідають діаграмам 𝐴𝑙, 𝐵𝑙, 𝐶𝑙, і 𝐷𝑙. 1) 𝐴𝑙 : Нехай 𝑒1, …,𝑒𝑙 +1 - ортонормований базис в ℝ𝑙 + 1, тобто <𝑒𝑖, 𝑒𝑗> = 𝛿𝑖𝑗. Покладемо 𝛼𝑖 = 𝑒𝑖 − 𝑒𝑖 + 1 (𝑖 = 1, 2, …, 𝑙). Тоді набір {𝛼1, …, 𝛼𝑙} лінійнонезалежний і <𝛼𝑖, 𝛼𝑖> = 2 (𝑖 = 1, 2, …, 𝑙), <𝛼𝑖, 𝛼𝑖 +1> = −1 (𝑖 = 1, 2, …, 𝑙 − 1), <𝛼𝑖, 𝛼𝑗> = 0, якщо 𝑗 ≠ 𝑖 – 1, 𝑖, 𝑖 + 1. Система {𝛼1, …, 𝛼𝑙} є 𝜋 – системою з діаграмою 𝐴𝑙. 2) 𝐵𝑙, 𝐶𝑙, 𝐷𝑙: Нехай 𝑒1, …, 𝑒𝑙 ортонормований базис в ℝ𝑙. Вважаючи 𝛼𝑙 = 𝑒𝑖 − 𝑒𝑖 + 1, 𝑖 = 1, 2, …, 𝑙 – 1, і для 𝐵𝑙: 𝛼𝑙 = 𝑒𝑙, для 𝐶𝑙: 𝛼𝑙 = 2𝑒𝑙, для 𝐷𝑙: 𝛼𝑙 = 𝑒𝑙 – 1 + 𝑒𝑙, отримаємо 𝜋 – системи з діаграмами 𝐵𝑙, 𝐶𝑙 і 𝐷𝑙. Фактично, всі діаграми Динкіна реалізуються як 𝜋 – системи.
|
||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 288; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.22.169 (0.034 с.) |
 , 𝐵 - її форма Кіллінга, 𝔥 – її підалгебра Картана і 𝑔 = 𝔥 + 𝑔 (𝛼) + 𝑔 (𝛽) + …, 𝔥 = 𝑔 (0) - її розклад по кореневим підпросторам. Позначимо через 𝔥* векторний простір, спряжений до 𝔥. Нехай 𝛥 ⊂ 𝔥* - множина всіх коренів {𝛼, 𝛽, … }; покладемо
, 𝐵 - її форма Кіллінга, 𝔥 – її підалгебра Картана і 𝑔 = 𝔥 + 𝑔 (𝛼) + 𝑔 (𝛽) + …, 𝔥 = 𝑔 (0) - її розклад по кореневим підпросторам. Позначимо через 𝔥* векторний простір, спряжений до 𝔥. Нехай 𝛥 ⊂ 𝔥* - множина всіх коренів {𝛼, 𝛽, … }; покладемо 
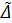 і 𝛼 + 𝛽 ≠ 0, то 𝐵 (𝑔 (𝛼), 𝑔 (𝛽)) = 0.
і 𝛼 + 𝛽 ≠ 0, то 𝐵 (𝑔 (𝛼), 𝑔 (𝛽)) = 0. (𝑋, 𝑌 ∈ 𝔥).
(𝑋, 𝑌 ∈ 𝔥). ′ +
′ +  ) = 𝐵 (𝐻, 𝐻′) −
) = 𝐵 (𝐻, 𝐻′) −  ,
,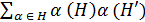 );
); .
. - векторний простір над ℚ, породжений 𝛥 в 𝔥*. Позначимо через 𝔥0 векторний простір над ℚ, породжений елементами 𝐻𝛼 (𝛼 ∈ 𝛥) із 𝔥. Легко побачити, що
- векторний простір над ℚ, породжений 𝛥 в 𝔥*. Позначимо через 𝔥0 векторний простір над ℚ, породжений елементами 𝐻𝛼 (𝛼 ∈ 𝛥) із 𝔥. Легко побачити, що 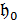 , вважаючи 𝜆1 > 𝜆2 (або 𝜆2 < 𝜆1), якщо існує номер 𝑘 (0 ≤ 𝑘 ≤ 𝑚 – 1), такий що 𝜆1 (𝐻1) = 𝜆2 (𝐻1), …, 𝜆1 (𝐻𝑘) = 𝜆2 (𝐻𝑘), і 𝜆1 (𝐻𝑘 + 1) > 𝜆2 (𝐻𝑘 + 1). В випадку, коли 𝜆 > 0, ми говоримо, що елемент 𝜆 додатній.
, вважаючи 𝜆1 > 𝜆2 (або 𝜆2 < 𝜆1), якщо існує номер 𝑘 (0 ≤ 𝑘 ≤ 𝑚 – 1), такий що 𝜆1 (𝐻1) = 𝜆2 (𝐻1), …, 𝜆1 (𝐻𝑘) = 𝜆2 (𝐻𝑘), і 𝜆1 (𝐻𝑘 + 1) > 𝜆2 (𝐻𝑘 + 1). В випадку, коли 𝜆 > 0, ми говоримо, що елемент 𝜆 додатній.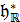 . Скалярний добуток в
. Скалярний добуток в 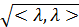 і для довільних 𝜆1 (≠ 0) і 𝜆2 (≠ 0) із
і для довільних 𝜆1 (≠ 0) і 𝜆2 (≠ 0) із 
 = {
= {  1, …,
1, …,  = 4 cos2𝛼𝑖𝛼𝑗.
= 4 cos2𝛼𝑖𝛼𝑗. =
=  = 1.
= 1. )=120o.
)=120o.