
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Физические Основы классической механикиСодержание книги Поиск на нашем сайте
Кинематика поступательного движения
• Кинематические уравнения движения
• Средняя скорость
за время • Средняя путевая скорость
за время • Мгновенная скорость
• Проекции скорости
• Модуль скорости
• Мгновенное ускорение
• Проекции ускорения на оси координат х, у,z
• Модуль ускорения
• Ускорение при криволинейном движении (по дуге окружности)
где
• Модули ускорений
• Уравнения равномерного и равнопеременного движений - равномерное движение: - равнопеременное движение “+” - равноускоренное, “ - “ - равнозамедленное Кинематика вращательного движения Положение твёрдого тела (при заданной оси вращения) задается углом поворота • Кинематическое уравнение вращательного движения • Мгновенная угловая скорость
• Угловое ускорение
• Связь линейных характеристик с угловыми линейная скорость - нормальное ускорение - тангенциальное ускорение - полное ускорение - • Уравнения равномерного и равнопеременного вращений
• Частота и период вращения: Частота (число оборотов в единицу времени) - Период Т (время одного полного оборота) - циклическая (круговая)частота - Связь циклической частоты с частотой Угол поворота
Задание 2. ЗАКОНЫ ДИНАМИКИ. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
Динамика Поступательного движения материальной точки Динамика – раздел механики, изучающий движение материальной точки (тела) с учетом сил, действующих на неё (него) со стороны других тел и полей. • Импульс материальной точки (тела)
• Второй закон Ньютона с учетом импульса в векторной форме
где • Второй закон Ньютона в скалярной форме
• Радиус-вектор и координаты центра масс: x c= где Закон движения центра масс: Третий закон Ньютона:
ЗАДАНИЕ 3. СИЛЫ ПРИРОДЫ. МЕХАНИКА СПЛОШНЫХ СРЕД • Сила гравитационного взаимодействия (закон всемирного тяготения)
где материальными точками. на глубине h от поверхности Земли: где g0 = 9,81 м/c2 –ускорение свободного падения у поверхности Земли. • Определение ускорения свободного падения у поверхности планет
где M- масса планеты, R – радиус планеты, ускорение свободного падения у поверхности Земли • Определение ускорения свободного падения тела, находящегося на некоторой высоте h от поверхности планеты
• Сила тяжести
• Космические скорости Первая космическая скорость Вторая космическая скорость • Сила упругости (закон Гука)
где
• Сила реакции опоры - обозначается Если материальная точка находится на горизонтальной поверхности, то • Сила трения скольжения
Энергия и законы сохранения • Кинетическая энергия материальной точки
• Потенциальная энергия материальной точки, находящейся в гравитационном поле Земли
• Потенциальная энергия сжатой (или растянутой) пружины
• Законы сохранения: Закон сохранения импульса Закон сохранения энергии • Законы сохранения для абсолютно упругого и неупругого ударов: Абсолютно упругий удар Закон сохранения импульса Закон сохранения энергии Абсолютно неупругий удар Закон сохранения импульса Закон сохранения энергии
Механика сплошных сред
ЗАДАНИЕ 4. ОСНОВНОЕ УРАВНЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА Динамика вращательного движения
Момент инерции тел правильной геометрической формы относительно неподвижной оси вращения
Момент силы, момент импульса. Основное уравнение динамики вращательного движения
ЗАДАНИЕ 5. МЕХАНИЧЕСКАЯ РАБОТА. МОЩНОСТЬ.
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 410; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.22.34 (0.01 с.) |

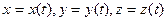 , где
, где  - время;
- время; , где
, где  - перемещение материальной точки
- перемещение материальной точки ;
; , где
, где  - путь, пройденный материальной точкой
- путь, пройденный материальной точкой , где
, где  - радиус вектор;
- радиус вектор; на оси координат х, у,z
на оси координат х, у,z ;
; ;
; , где
, где  ;
; ;
; ;
; ,
, - нормальное ускорение, направленное по радиусу к центру окружности;
- нормальное ускорение, направленное по радиусу к центру окружности; -тангенциальное ускорение, направленное по касательной к точке окружности;
-тангенциальное ускорение, направленное по касательной к точке окружности;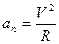 ,
,  ,
,  ;
; 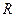 -радиус окружности;
-радиус окружности;

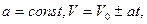
 ;
; .
. ;
; ;
; 
 ;
; 
 R – радиус окружности,
R – радиус окружности,
 ,
, ;
;
 - равномерное вращение;
- равномерное вращение;
 - равнопеременное вращение;
- равнопеременное вращение; ,
, ,
, ,
, ,
, , где N – число оборотов.
, где N – число оборотов. , где
, где  - масса м.т.,
- масса м.т.,  ,
,  ;
;  или
или  ,
, -сила, действующая на м.т.
-сила, действующая на м.т.
 , где
, где  - изменение импульса;
- изменение импульса; - импульс силы.
- импульс силы.
 ; yc =
; yc =  ; zc =
; zc = 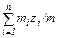 ,
,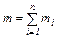


 ,
,
 - гравитационная постоянная
- гравитационная постоянная  - расстояние между
- расстояние между
 ,
,
 .
. .
. ,
, ,
,  .
. ,
,  ,
, - изменение размеров тела (удлинение),
- изменение размеров тела (удлинение),  - коэффициент упругости,
- коэффициент упругости, - напряжение в теле, возникающее за счет действия силы,
- напряжение в теле, возникающее за счет действия силы,  - площадь поперечного сечения тела,
- площадь поперечного сечения тела,  - относительное удлинение, Е – модуль Юнга (модуль упругости).
- относительное удлинение, Е – модуль Юнга (модуль упругости). .
. ;
; , где
, где  - коэффициент трения;
- коэффициент трения;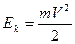 ,
,  ; где
; где 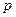 - импульс;
- импульс; , где
, где  - высота подъёма;
- высота подъёма; ; где
; где 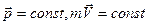 для замкнутых систем.
для замкнутых систем. для замкнутых систем;
для замкнутых систем; ;
; ;
; ;
; ;
;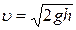 ,
где h – глубина, на которой находится отверстие относительно уровня жидкости в сосуде
,
где h – глубина, на которой находится отверстие относительно уровня жидкости в сосуде
 где η - коэффициент динамической вязкости жидкости;
где η - коэффициент динамической вязкости жидкости;
 - градиент скорости;
- градиент скорости;
 S - площадь соприкасающихся слоев
S - площадь соприкасающихся слоев
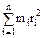 ,
где ri – расстояние i –й материальной точки массой m до оси вращения.
В случае непрерывного распределения масс: J =
,
где ri – расстояние i –й материальной точки массой m до оси вращения.
В случае непрерывного распределения масс: J =  .
Теорема Штейнера: момент инерции тела массой m относительно неподвижной оси вращения, не проходящей через центр масс и параллельный оси вращения:
J = Jz + mr2,
где Jz –момент инерции тела относительно оси z, проходящей через центр масс,
r - расстояние между осями.
.
Теорема Штейнера: момент инерции тела массой m относительно неподвижной оси вращения, не проходящей через центр масс и параллельный оси вращения:
J = Jz + mr2,
где Jz –момент инерции тела относительно оси z, проходящей через центр масс,
r - расстояние между осями.

 где
где 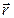 – радиус-вектор, проведенный из этой точки в точку приложения силы
– радиус-вектор, проведенный из этой точки в точку приложения силы  .
Модуль момента силы: M = Fl,
где l = r.sin α – плечо силы (кратчайшее расстояние между линией действия силы и осью вращения)
.
Модуль момента силы: M = Fl,
где l = r.sin α – плечо силы (кратчайшее расстояние между линией действия силы и осью вращения)
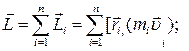
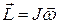 где
где  –радиус-вектор отдельной i - й частицы;
mi
–радиус-вектор отдельной i - й частицы;
mi  - импульс этой частицы;
J - момент инерции тела относительно оси;
- импульс этой частицы;
J - момент инерции тела относительно оси;  – угловая скорость
– угловая скорость

 где ε – угловое ускорение;
Jz -момент инерции тела относительно оси
где ε – угловое ускорение;
Jz -момент инерции тела относительно оси

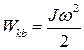 где J– момент инерции тела относительно оси,
ω - угловая скорость
Кинетическая энергия тела, катящегося по плоскости без скольжения:
где J– момент инерции тела относительно оси,
ω - угловая скорость
Кинетическая энергия тела, катящегося по плоскости без скольжения:
 где m – масса тела;
vc - скорость центра масс тела;
J – момент инерции тела относительно оси, проходящей через центр масс; ω –угловая скорость тела
где m – масса тела;
vc - скорость центра масс тела;
J – момент инерции тела относительно оси, проходящей через центр масс; ω –угловая скорость тела



