
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Направления: 190300.65 «Подвижной состав железных дорог»Содержание книги
Поиск на нашем сайте
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ» МИИТ
Одобрено кафедрой «Физика и химия»
ФИЗИКА Задания на контрольные работы № 1и №2 с методическими указаниями для студентов 1 курса Направления: 190300.65 «Подвижной состав железных дорог» (для всех специализаций)
Москва - 2012
Составители: канд. техн. наук, доц. Т.Ф. Климова ст. преп. В.Э. Геогджаев Рецензент: доктор физ.-мат. наук, проф. З. Л. Шулиманова
Курс физики играет важную роль в теоретической подготовке современного инженера - транспортника. Решение физических задач способствует формированию у студентов инженерного мышления, без которого невозможна успешная работа на транспорте, промышленных предприятиях и стройках. Цель методических указаний – оказать помощь студентам-заочникам в изучении курса физики. Предлагаемая работа состоит из двух частей, в каждой из них даны примеры решения задач, контрольные задания и общие методические указания. ОБЩИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ В процессе изучения физики студент должен выполнить четыре контрольные работы (по две на каждом курсе). Решение задач в контрольных работах является проверкой степени усвоения студентом теоретического курса, а рецензии на работу помогают доработать и правильно освоить различные разделы курса физики. Перед выполнением контрольной работы студенту необходимо внимательно ознакомиться с примерами решения задач по данной контрольной работе, уравнениями и формулами, приведенными в методических указаниях. В некоторых случаях преподаватель может дать студенту индивидуальное задание – задачи, не входящие в вариант студента. Выбор задач осуществляется по таблицам 1 и 2 следующим образом: первые четыре задачи выбираются по варианту, номер которого совпадает с последней цифрой учебного шифра, а пятая и шестая по варианту, номер которого совпадает с предпоследней цифрой шифра. Например, при шифре 1120–ПСс-1231 – студент решает в контрольной работе № 1 задачи 1, 11, 21, 31, 43, 53, в контрольной работе № 2 задачи 61, 71, 81, 91, 103, 113. Таблица 1. Задачи контрольной работы № 1
Таблица 2. Задачи контрольной работы № 2
Правила оформления контрольных работ и решения задач: 1. Условия всех задач студенты переписывают полностью без сокращений. 2. Все значения величин, заданных в условии и привлекаемых из справочных таблиц, записывают для наглядности сокращенно (столбиком) в тех же единицах, которые заданы, а затем рядом осуществляют перевод в единицы СИ. 3. Кроме задач на ядерные реакции (работа № 3), все задачи следует решать в СИ. 4. В большей части задач необходимо выполнять чертежи или графики с обозначением всех величин. Рисунки надо выполнять аккуратно, используя чертежные инструменты; объяснение решения должно быть согласовано с обозначениями на рисунках. 5. Необходимо указать физические законы, которые должны быть использованы, и аргументировать возможность их применения для решения данной задачи. 6. С помощью этих законов, учитывая условие задачи, получить необходимые расчетные формулы. 7. Вывод формул и решение задач следует сопровождать краткими, но исчерпывающими пояснениями. 8. Использованные в формулах буквенные обозначения должны быть согласованы с обозначениями, приведенными в условии задачи и на приведенном рисунке. Дополнительные буквенные обозначения следует сопровождать соответствующими объяснениями. 9. Получив расчетную формулу, необходимо проверить ее размерность.
Пример проверки размерности: [v] = 10. Основные физические законы, которыми следует пользоваться при решении задач (вывод расчетных формул), приведены в каждом из разделов. Там же приведены некоторые формулы, которыми можно пользоваться без вывода. 11. После проверки размерности полученных формул проводится численное решение задачи. 12. Вычисления следует производить по правилам приближенных вычислений с точностью, соответствующей точности исходных числовых данных условия задачи. Числа следует записывать в стандартном виде, используя множитель 10, например не 0,000347, а 3,47·10-4. 13. Каждая последующая задача должна начинаться с новой страницы. 14. В конце контрольной работы необходимо указать учебные пособия, учебники, использованные при ее выполнении, и дату сдачи работы и поставить подпись. 15. Если контрольная работа не допущена к зачету, то все необходимые дополнения и исправления сдают вместе с незачтенной работой. Исправления в тексте незачтенной работы не допускаются. 16. Допущенные к зачету контрольные работы с внесенными уточнениями предъявляются преподавателю на зачете. Студент должен быть готов дать во время зачета пояснения по решению всех выполненных задач.
Рекомендуемая литература Основная литература: 1. Т. И Трофимова. Курс физики: Учебное пособие. М.: Академия,, 2008 2. Т. И. Трофимова Краткий курс физики. М.: Высшая школа, 2009 3. Т.И Трофимова. Сборник задач по курсу физики с решениями М.: Высшая школа. 2008 4. А.А. Детлаф Курс физики. Учебное пособие. М.: Высшая школа, 2000 5. В.Ф. Дмитриева Основы физики. М. Высшая школа, 2001 6. В.Н. Недостаев. Физика. Конспект лекций т. 1-2. – М., РГОТУПС, 2005 Дополнительная литература: 7. С. Е Мельханов Общая физика. Конспект лекций, М.: Высшая школа, 2001 8. В.М. Гладской Физика. Сборник задач с решениями, М.:Дрофа, 2004 9. Т.И. Трофимова Физика.. 500 основных законов и формул. М., Высшая школа, 2003 10. В. Ф. Дмитриева, В. Ф. Прокофьев. Основы физики. М.: Высшая школа, 2002 11. Физический энциклопедический словарь. М.: Российская энциклопедия, 2003 12. С.М. Кокин, В.А. Селезнев Физика на транспорте. М.: 1995
КОНТРОЛЬНАЯ РАБОТА № 1. Задание 2. ЗАКОНЫ ДИНАМИКИ. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
Динамика ЗАДАНИЕ 3. СИЛЫ ПРИРОДЫ. МЕХАНИКА СПЛОШНЫХ СРЕД • Сила гравитационного взаимодействия (закон всемирного тяготения)
где материальными точками. на глубине h от поверхности Земли: где g0 = 9,81 м/c2 –ускорение свободного падения у поверхности Земли. • Определение ускорения свободного падения у поверхности планет
где M- масса планеты, R – радиус планеты, ускорение свободного падения у поверхности Земли • Определение ускорения свободного падения тела, находящегося на некоторой высоте h от поверхности планеты
• Сила тяжести
• Космические скорости Первая космическая скорость Вторая космическая скорость • Сила упругости (закон Гука)
где
• Сила реакции опоры - обозначается Если материальная точка находится на горизонтальной поверхности, то • Сила трения скольжения
Энергия и законы сохранения • Кинетическая энергия материальной точки
• Потенциальная энергия материальной точки, находящейся в гравитационном поле Земли
• Потенциальная энергия сжатой (или растянутой) пружины
• Законы сохранения: Закон сохранения импульса Закон сохранения энергии • Законы сохранения для абсолютно упругого и неупругого ударов: Абсолютно упругий удар Закон сохранения импульса Закон сохранения энергии Абсолютно неупругий удар Закон сохранения импульса Закон сохранения энергии
Механика сплошных сред
ЗАДАНИЕ 4. ОСНОВНОЕ УРАВНЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА Динамика вращательного движения
Момент инерции тел правильной геометрической формы относительно неподвижной оси вращения
Момент силы, момент импульса. Основное уравнение динамики вращательного движения
ЗАДАНИЕ 5. МЕХАНИЧЕСКАЯ РАБОТА. МОЩНОСТЬ. ЗАДАНИЕ 6. ЗАКОНЫ СОХРАНЕНИЯ ПРИ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ Закон сохранения момента импульса. Работа при вращении тела. Кинетическая энергия вращательного движения.
Аналогия между формулами поступательного и вращательного движения.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КОНТРОЛЬНАЯ РАБОТА № 1 Пример 1. Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид х = А + В t + С t3, где А = 4 м, В = 2 м/с, С = - 0,5 м/с2. Для момента времени t1 = 2 с определить: 1) координату х1 точки; 2) мгновенную скорость V1; 3) мгновенное ускорение а1. Дано: х = А + В t + С t3 А = 4 м В = 2 м/с С = - 0,5 м/с2. t1 = 2 с _____________ х1-? V1-? а1-?
Решение. Найдем координату точки, для которой известно кинематическое уравнение движения, подставив в уравнение движения вместо t заданное значение t1: х1 = А + В t1 + С t13; х1 = 4 м. Мгновенную скорость V в произвольный момент времени t найдем, продифференцировав координату х по времени: V = Тогда в заданный момент времени мгновенная скорость: V1 = B + 3Ct21; Мгновенное ускорение в произвольный момент времени найдем, взяв вторую производную от координаты по времени: a = Вычисления: Скорость V1 = - 4 м/с. Знак минус указывает на то, что в момент времени t1 = 2 с точка движется в отрицательном направлении координатной оси.
Мгновенное ускорение в заданный момент времени равно: a1 = - 6 м/c2, Знак минус указывает на то, что направление вектора ускорения совпадает с отрицательным направлением координатной оси.
Ответ: V1 = - 4 м/с, a1 = - 6 м/c2
Пример 2. Тело вращается вокруг неподвижной оси по закону, выражаемому формулой φ = 10 + 20 t - 2 t2 ( рис. 1). Найдите по величине и направлению полное ускорение точки, находящейся на расстоянии R = 0,1 м от оси вращения, для момента времени t1 = 4 с.
Условие: φ=10+20t-2t2; R =0,1 м; t1 =4 c; a -? α -? Решение. Точка вращающегося тела описывает окружность. Полное ускорение точки определяется геометрической суммой тангенциального и нормального ускорения: Тангенциальное и нормальное ускорения точки вращающегося тела выражаются формулами: а t = εR; (2) an = ω2R, (3) где ω - угловая скорость тела; ε - его угловое ускорение; R - расстояние от оси вращения. Подставляя выражения аt и аn в формулу (1) находим: a = R Угловая скорость вращающегося тела равна первой производной от угла поворота по времени ω = В момент времени t = 4 с угловая скорость ω = 4 с-1. Угловое ускорение вращающегося тела равно первой производной от угловой скорости по времени: ε = Подставляя найденные и заданные значения в формулу (4) получим: a = 1,65 м/c2. Направление полного ускорения можно определить, если найти углы, которые векторы ускорения составляют с касательной к траектории или нормалью к ней: cos α = Вычисления: По формулам (2) и (3) найдем значения аt и an: at = - 0,4 /c2; an = 1,6 /c2. Подставив эти значения и значения полного ускорения в формулу (5), получим: cos α = 0,242; α = 760.
Ответ: a = 1,65 м/c2, α = 760
Условие: m =1000 кг; S=200 м; sina =0,1 μ=0,05; v0 =0; vк =54км/ч = 15м/с; F -?
Решение. Автомобиль движется равноускоренно, причем начальная скорость равна нулю. Выберем ось х, расположенную вдоль наклонной плоскости, ось у – перпендикулярно ей (рис. 3). На автомобиль действует четыре силы: сила тяжести FТ =m g, сила реакции опоры N, сила тяги F и сила трения FТР. Запишем основной закон динамики:
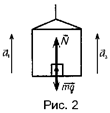
Это уравнение в проекциях на оси координат на ось х: ma = F – mg sina - FTP, на ось у: 0 = N – mg cosa, FTP = μ N. соsa= Выразим из этих уравнений силу тяги F F = mg sina + μmg cosa + ma. Ускорение на этом участке равно: a = (vk 2 - v02)/(2s) = vk2/(2s). Найдем силу тяги двигателя на этом участке: F = mg sinα + μmg cosα + Вычисления: F = 1000(0.98+0,50+0,56) = 2043(Н) Ответ: F =2043(Н) Пример 4. На горизонтальной платформе шахтной клети стоит человек массой m = 60 кг. Определить силу давления человека на платформу: 1) при ее подъеме с ускорением а1 = 3 м/с2; 2) при равномерном подъеме и спуске; 3) при спуске с ускорением а3 = 9,8 м/с2.
m=60 кг; а1=3 м/с2; v2=const, a2=0; а3=9,8 м/с; F1-? F2 -? F3 -?
Решение. На человека, стоящего на платформе шахтной клети действуют две силы: сила тяжести m g и сила реакции опоры N. Согласно второму закону Ньютона:
Согласно третьему закону Ньютона сила давления человека на платформу равна силе реакции опоры:
1. Согласно рис. 2 запишем уравнение (1) в проекции на ось У ma1 = N1 – mg Учитывая (2) получим
F1 = N1 = m (g + a1),
2. При равномерном движении шахтной клети а2 = 0 и, следовательно, сила давления человeка на платформу равна силе тяжести: F2 = N2 = mg. 3. При спуске платформы с ускорением, направленным вниз уравнение движения платформы имеет вид ma3 = mg – N3. Откуда сила давления человека на платформу: F3 = N3 = =m(g – a3). Учитывая, что а3 = g имеем F3 = 0. Следоватeльно, человек не давит на платформу.
Вычисления: F1 = 783 H, F2 = 60·9,81=588,6 (Н), F3 = 0. Ответ: F1 = 783 H, F2 = 588,6 (Н), F3 = 0.
Пример 5. Каким был бы период обращения ИСЗ на круговой орбите, если бы он был удален от поверхности Земли на расстояние, равное земному радиусу (R = 6400 км). Условие: h = R = 6370 км; Т -?
Решение. Период обращения ИСЗ по круговой орбите
Для определения скорости спутника учтем, что при его движении по круговой орбите на спутник действует только сила притяжения Земли Ft, сообщающая ему нормальное ускорение:
Ft = Fn;
где G – гравитационная постоянная, m – масса спутника, M – масса Земли.
Отсюда скорость спутника равна
Учитывая, что
где g – ускорение силы тяжести на поверхности Земли, получаем
Подставляя это значение скорости в формулу периода, найдем, что
Вычисление: Т = Ответ: Т = 3 ч 59 мин.
Пример 6. Стальная прoвoлока сечением S= 3 мм2 под действием растягивающей силы, равной F = 4 . 104 Н имеет длинy L1 = 2 м. Определить абсолютное удлинение проволоки при увеличении растягивающей силы на F1 = 104 Н. Модуль Юнга стали Е =2 . 1011 Па. Условие: Е = 2·1011 Па; S = 3 мм2 =3·10-6 м2; L1 = 2 м; F = 4·104 Н; F1 =1,0·104 Н; ΔL2 -?
Решение. Для того чтобы найти абсолютное удлинение проволоки при увеличенной растягивающей силе, необходимо узнать ее первоначальную длину L. Из закона Гука
F = εE = E(L1 – L)S/L
находим L = EL1S/(F +ES). При увеличении растягивающей силы на величину F1
F + F1 = EΔL2S/L. Откуда ΔL2 = (F + F1)L/ES. Заменив L выражением, записанным выше, получаем
ΔL2 = (F + F1)L1/(F + ES). Проверка размерности:
Вычисление: ΔL2 = ( 4·104 + 1,0·104 )2/( 4·104 + 2·10113·10-6 )=0,16(м)
Ответ: ΔL2 = 0, 16 м. Пример 7. Маховик, массу которого m = 5 кг можно считать распределенной по ободу радиуса r = 20 см, свободно вращается вокруг горизонтальной оси, проходящей через его центр с частотой n = 720 мин-1. При торможении маховик останавливается через Δt = 20 с. Определить тормозящий момент М и число оборотов N, которое сделает маховик до полной остановки. Условие: m = 5 кг r = 20см =0,20 м n =720 мин-1 = 12 с-1 Δt =20 с М -? N -? Решение. Если тормозящий момент постоянен, то движение маховика равнозамедленное, и основное уравнение динамики вращательного движения можно записать в виде:
где Число оборотов N может быть найдено как кинематически, так и по изменению кинетической энергии, равному работе совершаемой тормозящей силой. Векторному уравнению (1) соответствует скалярное уравнение J∆ω = M∆t, (2) где ∆ω, M - модули соответствующих векторов. Из условия задачи следует, что ∆ω = |ω – ω0 | = ω0 =2πn (3) Поскольку масса маховика распределена по ободу, момент инерции J = mr2 (4)
Подставляя выражения (2), (3) в (1) получим mr22πn = M∆t. Откуда M = 2πnmr2/Δt. Векторы Угловое перемещение, пройденное маховиком до остановки φ = ω0∆t – ε∆t2/2. (5) Учитывая, что ω = ωo - ε∆t = 0 преобразуем выражение (6) φ = ω0∆t/2. Так как φ = 2πN, ω =2πn, где N - число оборотов, которое делает маховик до полной остановки, окончательно получим N = nt/2
Проверяем размерность: Вычисления: М = 2·3,14·5·0,04/20 = 0,75 (Дж) N = 12·20/2=120 (об) Ответ: М = 0,75 Дж, N = 120 об.
Условие: m =2000 кг; S=100 м; α= 150; μ=0,05; v0 =0; vк =36км/ч = 10м/с; Рср -? Рmax -?
Решение. Автомобиль движется равноускоренно, причем начальная скорость равна нулю. Выберем ось х, расположенную вдоль наклонной плоскости, ось у – перпендикулярно ей (рис. 3). На автомобиль действует четыре силы: сила тяжести FТ =m g, сила реакции опоры N, сила тяги F и сила трения FТР. Запишем основной закон динамики:
Это уравнение в проекциях на оси координат на ось х: ma = F – mg sina - FTP, на ось у: 0 = N – mg cosa, FTP = μ N= μ mg cosa, Выразим из этих уравнений силу тяги F F = mg sina + μmg cosa + ma. Ускорение на этом участке равно: a = (vk 2 - v02)/(2s) = vk2/(2s). Найдем силу тяги двигателя на этом участке: F = mg sinα + μmgcosα + Работа двигателя на этом участке: A = Fscosφ, Где φ– угол между F и s, равный нулю. Следовательно A = Fs Подставив сюда выражение для F, получим А = m(gsinα + μgcosα + Средняя мощность равна < P> =
Максимальная мощность автомобиля достигается в тот момент, когда скорость максимальна: Pmax = F·vk, Проверка размерности: Вычисление: < P> = 3,58·104 Вт, Pmax = 7·104 Вт. Ответ: < P> = 3,58·104 Вт, Pmax = 7·104 Вт.
Пример 9. На скамье Жуковского сидит человек и держит в вытянутых руках гири массой m =10 кг каждая. Расстояние от каждой гири до оси вращения скамьи l 1 = 50 см. Скамья вращается с частотой n1 = 1,0 с-1. Как изменится частота вращения скамьи и какую работу A произведет человек, если он сожмет руки так, что расстояние от каждой гири до оси уменьшится до l 2 = 20 см. Суммарный момент инерции человека и скамьи относительно оси вращения J =2,5 кг·м2. Ось вращения проходит через центр масс человека и скамьи. Условие: m = 10 кг; l 1=50 см = 0,5 м; n1 =1,0 с-1; l 2 =20 см =0,2 м; J = 2,5 кг·м2. n2 -? А -? Решение. Частота вращения скамьи Жуковского изменится в результате действий, производимых человеком при сближении гирь. В системе тел скамья – человек – гири все силы, кроме сил реакции опоры, являются внутренними и не изменяют момента импульса системы. Однако моменты сил реакции опоры относительно вертикальной оси равны нулю. (Для скамьи Жуковского силы трения в оси можно считать отсутствующими.) Следовательно, момент импульса этой системы остается постоянным:
где J1ω1, J2ω2 - моменты импульса системы соответственно до и после сближения гирь. Перепишем векторное уравнение (1) в скалярном виде: J1ω1 = J2ω2. (2) До сближения гирь момент инерции всей системы: J1 = J0 + 2ml12. После сближения: J2 = J0 + 2ml22, где m - масса каждой гири. Выражая угловую скорость через частоту вращения по формуле ω = 2πn и подставляя ее в уравнение (1) получаем (J0 + 2ml12)n1 = (J0 + 2ml22)n2. Откуда
Все внешние силы не создают вращающего момента относительно оси и, следовательно, не совершают работы. Поэтому изменение кинетической энергии системы равно работе, совершенной человеком:
A = W2 - W1 = Учитывая, что ω2 = J1ω1/J2, получаем работу, совершаемую человеком:
Проверка размерности:
Вычис |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 369; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.241.87 (0.015 с.) |


 ,
,
 - гравитационная постоянная
- гравитационная постоянная  - расстояние между
- расстояние между
 ,
,
 .
. .
. ,
, ,
, 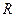 - радиус планеты;
- радиус планеты; .
. ,
,  ,
, - изменение размеров тела (удлинение),
- изменение размеров тела (удлинение),  - коэффициент упругости,
- коэффициент упругости, - напряжение в теле, возникающее за счет действия силы,
- напряжение в теле, возникающее за счет действия силы,  - площадь поперечного сечения тела,
- площадь поперечного сечения тела,  - относительное удлинение, Е – модуль Юнга (модуль упругости).
- относительное удлинение, Е – модуль Юнга (модуль упругости). .
. ;
; , где
, где  - коэффициент трения;
- коэффициент трения;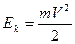 ,
,  ; где
; где 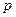 - импульс;
- импульс; , где
, где  - высота подъёма;
- высота подъёма; ; где
; где 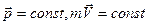 для замкнутых систем.
для замкнутых систем. для замкнутых систем;
для замкнутых систем; ;
; ;
; ;
; ;
;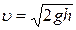 ,
где h – глубина, на которой находится отверстие относительно уровня жидкости в сосуде
,
где h – глубина, на которой находится отверстие относительно уровня жидкости в сосуде
 где η - коэффициент динамической вязкости жидкости;
где η - коэффициент динамической вязкости жидкости;
 - градиент скорости;
- градиент скорости;
 S - площадь соприкасающихся слоев
S - площадь соприкасающихся слоев
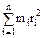 ,
где ri – расстояние i –й материальной точки массой m до оси вращения.
В случае непрерывного распределения масс: J =
,
где ri – расстояние i –й материальной точки массой m до оси вращения.
В случае непрерывного распределения масс: J =  .
Теорема Штейнера: момент инерции тела массой m относительно неподвижной оси вращения, не проходящей через центр масс и параллельный оси вращения:
J = Jz + mr2,
где Jz –момент инерции тела относительно оси z, проходящей через центр масс,
r - расстояние между осями.
.
Теорема Штейнера: момент инерции тела массой m относительно неподвижной оси вращения, не проходящей через центр масс и параллельный оси вращения:
J = Jz + mr2,
где Jz –момент инерции тела относительно оси z, проходящей через центр масс,
r - расстояние между осями.

 где
где 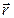 – радиус-вектор, проведенный из этой точки в точку приложения силы
– радиус-вектор, проведенный из этой точки в точку приложения силы  .
Модуль момента силы: M = Fl,
где l = r.sin α – плечо силы (кратчайшее расстояние между линией действия силы и осью вращения)
.
Модуль момента силы: M = Fl,
где l = r.sin α – плечо силы (кратчайшее расстояние между линией действия силы и осью вращения)
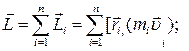
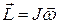 где
где  –радиус-вектор отдельной i - й частицы;
mi
–радиус-вектор отдельной i - й частицы;
mi  - импульс этой частицы;
J - момент инерции тела относительно оси;
- импульс этой частицы;
J - момент инерции тела относительно оси;  – угловая скорость
– угловая скорость

 где ε – угловое ускорение;
Jz -момент инерции тела относительно оси
где ε – угловое ускорение;
Jz -момент инерции тела относительно оси

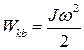 где J– момент инерции тела относительно оси,
ω - угловая скорость
Кинетическая энергия тела, катящегося по плоскости без скольжения:
где J– момент инерции тела относительно оси,
ω - угловая скорость
Кинетическая энергия тела, катящегося по плоскости без скольжения:
 где m – масса тела;
vc - скорость центра масс тела;
J – момент инерции тела относительно оси, проходящей через центр масс; ω –угловая скорость тела
где m – масса тела;
vc - скорость центра масс тела;
J – момент инерции тела относительно оси, проходящей через центр масс; ω –угловая скорость тела
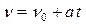


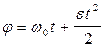

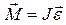
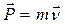

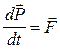





 = B + 3Ct2.
= B + 3Ct2. = 6Ct, т.е. a1 = 6Ct1
= 6Ct, т.е. a1 = 6Ct1
 (1)
(1)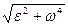 . (4)
. (4) = 20 – 4t.
= 20 – 4t. = - 4 c-2.
= - 4 c-2.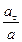 . (5)
. (5) Пример 3. Автомобиль массой m = 1000 кг движется вверх по наклонной плоскости с уклоном 0,1, развивая на пути S = 200 м скорость vк = 54 км/ч. Коэффициент трения μ = 0,05. Определить силу тяги двигателя
Пример 3. Автомобиль массой m = 1000 кг движется вверх по наклонной плоскости с уклоном 0,1, развивая на пути S = 200 м скорость vк = 54 км/ч. Коэффициент трения μ = 0,05. Определить силу тяги двигателя .
.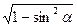
 = m(g sin α + μg cos α +
= m(g sin α + μg cos α +  )
) Условие:
Условие: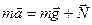 . (1)
. (1) N N = F (2)
N N = F (2) .
.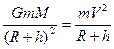
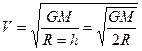

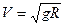
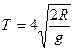
 14360 (с) = 3 ч 59 мин
14360 (с) = 3 ч 59 мин .
. (1)
(1) - изменение угловой скорости за интервал времени ∆t; М – искомый тормозящий момент.
- изменение угловой скорости за интервал времени ∆t; М – искомый тормозящий момент. направлены в сторону противоположную вектору
направлены в сторону противоположную вектору 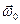 .
.
 , где
, где  , откуда
, откуда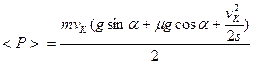

 ;
;  , (1)
, (1) 2,3 c-1.
2,3 c-1. .
.
 ,
, 



