
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Белицкий В.Д., Кожушко А.А., Панин Ю.Н., Пахотин А.Н.Стр 1 из 5Следующая ⇒
Белицкий В.Д., Кожушко А.А., Панин Ю.Н., Пахотин А.Н. Гидравлика и нефтегазовая Гидромеханика Методические указания
Омск Издательство ОмГТУ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Омский государственный технический университет» Кафедра: «Нефтегазовое дело» В.Д. Белицкий, Кожушко А.А., Панин Ю.Н., Пахотин А.Н. Гидравлика и нефтегазовая гидромеханика Методические указания Направление подготовки бакалавров 131000.62 «Нефтегазовое дело» Омск – 2014 ПРАВИЛА ИСПОЛЬЗОВАНИЯ ЕДИНИЦ ФИЗИЧЕСКИХ ВЕЛИЧИН
При выполнении расчетов значения физических величин должны выражаться в единицах международной системы СИ или в единицах, допускаемых к применению ГОСТ 8.417 – 2002. Таблица 1.1 Основные единицы международной системы СИ
Таблица 1.2 Важнейшие производные единицы системы СИ
Таблица 1.3 Приставки для кратных и дольных единиц измерения
Таблица 1.4 Соотношения между единицами давления
Таблица 1.5 Соотношения между единицами вязкости
ГИДРОСТАТИКА Вопросы для самопроверки
1. Каково численное соотношение между единицами давления «Паскаль» и «Техническая атмосфера»? 2. Какие виды давления вы знаете, и какими приборами они измеряются? 3. Как запишется основное уравнение гидростатики, если известно давление р0 на свободной поверхности жидкости, и требуется определить абсолютное давление в точке расположенной ниже? 4. Где расположена пьезометрическая поверхность для открытого сосуда с жидкостью? 5. Чему равно нормальное атмосферное давление?
Примеры решения задач Пример 2.1. В закрытом резервуаре с нефтью плотностью Определить показания манометра Решениe Проведем плоскость 1-1 на уровне присоединения манометра. В этой плоскости абсолютное давление в соответствии с основным Рис 2.4 уравнением гидростатики (2.3) равно
где р0 – абсолютное давление на поверхности, равное Тогда Поскольку манометр показывает избыточное давление, то
Так как на поверхности жидкости давления меньше атмосферного, то пьезометрическая высота отрицательна:
и пьезометрическая плоскость расположена ниже поверхности жидкости на расстоянии 1,37м.
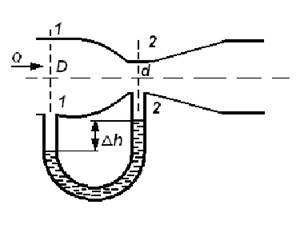
Задача 2.1. Определить разность давлений в сечениях 1 и 2 горизонтального водопровода по разности высот жидкости в трубках ртутного дифференциального манометра h=150мм (рис. 2.5) Рис. 2.5 Задача 2.2. Избыточное давление в нефтяном пласте составляет 4,9 МПа. Можно ли предотвратить выброс нефти из скважины, заполнив ее глинистым раствором плотностью
Рис. 2.6. 740мм.рт.ст.
Задача 2.4. Барометр, установленный у подножия холма, показывает давление 760мм.рт.ст, на вершине холма – 720мм.рт.ст. Определить высоту холма, считая температуру воздуха одинаковой и равной 100С. Газовая постоянная для воздуха R=287 Дж/кг0К. Задача 2.5. Определить на какой высоте Н от уровня моря давление воздуха составит 690мм.рт.ст. Температуру воздуха считать постоянной и равной 200С. Давление воздуха на уровне моря принять соответствующим 760мм.рт.ст.
Вопросы для самопроверки
1. Как определяется равнодействующая сил давления на твердую поверхность и что понимается под символом рс? 2. Может ли равнодействующая сил давления действовать с внешней стороны твердой поверхности, где жидкости нет? 3. Что такое центр давления? 4. Может ли центр давления располагаться выше центра тяжести смоченной части плоской поверхности?
Примеры решения задач
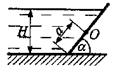
Пример 2.3. Вертикальная стенка (рис.2.8) длиной
Рис.2.8.
Найти величину опрокидывающего момента, действующего на стенку, а также определить будет ли стенка устойчива против опрокидывания, если плотность материала стенки Решение Найдем силу давления воды на стенку слева. Так как на поверхности давление атмосферное, то пьезометрическая плоскость совпадает с поверхностью жидкости
Координаты центра давления
Для прямоугольной стенки
Точно также справа
Опрокидывающий момент, т.е. момент сил давления жидкости относительно точки О (см.рис.2.8):
Восстанавливающим моментом против опрокидывания стенки будет момент силы тяжести относительно точки О:
Так как Мвос>Мопр, то стенка устойчива.
Задачи для самостоятельного решения
Задача 2.6. Найти силу давления воды на дно сосуда диаметром D=1м (рис.2.9), если глубина Н=0,7м, вес поршня G=300Н, d=0,5м.
Рис. 2.9. Рис. 2.10.
Задача 2.7. Наклонный прямоугольный щит плотины шарнирно закреплен на оси О (рис. 2.11). При каком уровне воды Н щит опрокинется, если угол наклона щита
Вопросы для самопроверки
1. В чем сходство и различие формул для определения горизонтальной составляющей силы давления жидкости на криволинейную поверхность и силой давления на плоскую поверхность? 2. Что называется «телом давления»? 3. Если тело тонет, то куда направлена Архимедова сила? Примеры решения задач
Пример 2.5. Определить вес груза, установленного на круглом в плане металлическом понтоне диаметром d=4м, если после установки на него груза осадка понтона увеличилась на h=0,6м.
Решение
Вес груза равен весу вытесненной понтоном воды на основании закона Архимеда
Следовательно, вес груза будет равен
Пример 2.6. Определить необходимый объем W заполненного светильным газом воздушного шара, поднимающего на уровне земли груз весом G=1000Н (вместе с весом шара), если
Решение
Подъемная сила воздуха Рвыт, действующая на шар по закону Архимеда, уравновешивается весом шара с грузом G и весом газа в нем
Задачи для самостоятельного решения
Рис. 2.18. Длина спущенных труб – 1000м, их внешний диаметр – 73мм, толщина стенок – 5,5мм, вес одного метра длинны – 93,7 Н. Определить максимальные усилия на крюке лебедки для двух случаев: 1) нижний конец труб открыт; 2) нижний конец труб заглушен.
Задача 2.14. Какой объем бензина (
ГИДРОДИНАМИКА ЛАБОРАТОРНАЯ РАБОТА № 1 Цели и задачи работы. Целью лабораторной работы является иллюстрация уравнения Бернулли на экспериментной установке. Задачи работы 1. С помощью пьезометров и трубок Пито определить пьезометрический напор (удельную энергию давления), полный напор (полную удельную энергию) установившегося потока жидкости в канале переменного сечения. 2. Определить потери напора, пьезометрический и гидравлический уклоны на характерных участках трубопровода. 3. Построить пьезометрическую и гидродинамическую линии для установившегося движения жидкости.
4. Определить скорость и расход жидкости. 5. Найти постоянную расходомера Вентури и построить его тарировочную характеристику.
Порядок выполнения работы Подготовить установку для проведения опытов. Для этого закрыть кран 5, расположенный на выходе из трубы переменного сечения. Заполнить напорный резервуар 2 до заданного уровня. Затем плавно открывая кран 5, установить малый расход и после достижения установившегося режима течения, произвести замеры необходимых величин. Увеличивая расход, повторить опыт ещё три раза. Режимы опытов рекомендуется брать такими, чтобы скоростной напор в наиболее узком сечении трубы переменного сечения находился в пределах 5-15 см. При установлении режима опыта необходимо следить за тем, чтобы в резервуаре 2 обеспечивался постоянный напор Результаты замеров занести в таблицу 3.2 Таблица 3.2
ЛАБОРАТОРНАЯ РАБОТА № 2. Задачи работы 1.1.Ознакомиться с режимами движения жидкости: ламинарным и турбулентным. 1.2.Опытным путем установить режим движения жидкости. ЛАБОРАТОРНАЯ РАБОТА № 3 ИССЛЕДОВАНИЕ ПОТЕРЬ НАПОРА ПО ДЛИНЕ ТРУБОПРОВОДА Задачи работы 1.1 Определить опытным путем величину потерь напора по длине трубопровода и коэффициент путевых потерь (коэффициент Дарси) для указанных участков трубопровода. 1.2 Расчетным путем определить коэффициенты путевых потерь и сравнить их с опытными значениями. 1.3 Исследовать изменение потерь напора по длине трубопровода в зависимости от скорости движения жидкости. Порядок выполнения работы Включить установку и заполнить рабочей жидкостью напорный резервуар 11. Опыты начинаются с малого расхода, при этом должно обеспечиваться постоянство уровня жидкости в резервуаре с помощью кранов 7 и 8. Установить расход, измерить уровень жидкости в пьезометрах и с помощью мерного бака определить расход жидкости в трубопроводе 3. Показания пьезометров заносятся в табл. 3.7, а уровень жидкости в мерном баке и время его наполнения- в табл. 3.8. Расход жидкости определяется по формуле
где W - объем жидкости в мерном баке, см3; t - время наполнения бака, с. Объем жидкости в мерном баке определяется по шкале 4 и тарировочному графику мерного бака (рис. 3.5). Опыты повторить 2-3 раза, постепенно увеличивая расход жидкости в трубопроводе 3. Таблица 3.7
Таблица 3.8
Определим расход Q в трубопроводе:
где W - объем в мерном баке, см3; t-время заполнения бака, с. Объем в напорном баке определяют по тарировочному графику (см. рис.3.5). Вычисляем среднюю скорость движения жидкости в трубопроводе:
где S - площадь живого сечения трубопровода, см2; Определяем скоростной напор V2/2g, см. На основе опытных данных (по показаниям пьезометров) определяем потери напора по длине h h Так как рассматриваются участки трубопровода постоянного сечения, то скоростные напоры двух сечений будут одинаковы. Поэтому потери напора по длине h Опытное значение коэффициента путевых потерь
где h Для каждого из проведенных опытов определяется коэффициент путевых потерь (Дарси)
где По табл. 3.4 определяем кинематический коэффициент вязкости Определяем режим движения жидкости в трубопроводе и по известным зависимостям гидравлики находим значение коэффициента путевых потерь для ламинарного режима:
для турбулентного режима:
Данные расчетов заносим в табл. 3.8. По результатам опытов строим графическую зависимость
Рис. 3.5. Тарировочный график мерного бака. Контрольные вопросы 1.От каких параметров зависят потери напора по длине трубопровода? 2.Как влияет режим движения жидкости на потери напора по длине? 3.Как опытным путем определяется коэффициент Дарси? 4.По каким формулам производится определение коэффициента Дарси для ламинарного и турбулентного режимов движения жидкости? 5.Как определяются потери давления по длине трубопровода? 6.Влияет ли расход жидкости на потери напора по длине?
ЛАБОРАТОРНАЯ РАБОТА № 4 ИССЛЕДОВАНИЕ ПОТЕРЬ НАПОРА В МЕСТНЫХ СОПРОТИВЛЕНИЯХ Задачи работы 1.1. Определить опытным путем потери напора в местных сопротивлениях и коэффициенты местных сопротивлений. 1.2. Расчетным путем найти коэффициенты местных сопротивлений при внезапном расширении потока и сравнить с опытными значениями. Порядок выполнения работы Эта работа проводится на той же установке (рис. 3.4), что и лабораторная работа № 3. Запустить установку и заполнить напорный резервуар 2 и горизонтально расположенный трубопровод 5. При установившемся движении жидкости с помощью мерного бака и секундомера определить расход Q и записать показания пьезометров hi; перед местным сопротивлением и hi+1 после местного сопротивления в табл.3.9. Определяем среднюю скорость движения жидкости перед местным сопротивлением и за местным сопротивлением. Средняя скорость жидкости определяется по формуле
где
Определяем скоростной напор Находим разность показаний пьезометров
где hi; - показание параметра перед местным сопротивлением, см; hi+1 - показание параметра за местным сопротивлением, см. Определяем опытное значение потерь напора по формуле
где Vi - средняя скорость перед местным сопротивлением, см/с;Vi+1 -средняя скорость за местным сопротивлением, см/с; g — ускорение свободного падения, см/с2. Опытное значение коэффициента местного сопротивления определяем по формуле
где V - наибольшее значение средней скорости из Vi и Vi+1, см/с. Теоретическое значение коэффициента местных сопротивлений вычисляем по зависимости
где S2 - значение площади живого сечения трубопровода широкой части, см2; S1 - значение площади живого сечения трубопровода в узкой части, см2. Данные опытов обрабатываются и записываются в табл. 3.9. Таблица 3.9
По результатам опытов построить графическую зависимость Сравниваем результаты полученных значений
Контрольные вопросы 1.Что называется местным сопротивлением? 2.Назовите примеры местных сопротивлений. 3.По какой формуле определяются потери напора в местном сопротивлении? 4.Как определить опытным путем значение коэффициента местного сопротивления? 5.От каких параметров зависят потери напора в местном сопротивлении? 6.Являются ли гидродвигатель, дроссель, другие элементы гидропривода примерами сложных местных сопротивлений? 7.Как найти потери давления в местном сопротивлении, если известны потери напора? 8.Как определяется средняя скорость потока жидкости? 9.Что понимается под принципом наложения потерь?
Библиографический список 1. Альтшуль А.Д., и др. Гидравлика и аэродинамика. – М.: Стройиздат, 1987. – 414с. 2. Башта Т.М., Руднев С.С. и др. Гидравлика, гидромашины и гидроприводы. – М.: Машиностроение, 1982. -423с. 3. Башта Т.М. Машиностроительная гидравлика: Справочник. – М.: Машиностроение, 1971.-672с. 4. Транспорт и хранение нефти и газа в примерах и задачах: Учебное пособие /Под общей редакцией Ю.Д. Земенкова. – СПб.: Недра, 2004. – 544с. 5. Идельчик А.Е. Справочник по гидравлическим сопротивлениям. – М.: Машиностроение, 1975. – 560с. 6. Лабораторные работы по гидравлике (технической гидромеханике) на установках типа ГД: Методические указания / Сост.: С.П. Лупинос, Ш.К. Мукушев, Н.А. Угрюмов, Д.В. Поступинских; СибАДИ. – Омск, 2003. – 32с. 7. Басниев К.С., Дмитриев Н.М., Розенберг Г.Д.. Нефтегазовая гидромеханика: Учебник для вузов. – Москва – Ижевск, 2003, 480 с.
Белицкий В.Д., Кожушко А.А., Панин Ю.Н., Пахотин А.Н. Гидравлика и нефтегазовая Гидромеханика Методические указания
Омск Издательство ОмГТУ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Омский государственный технический университет»
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 934; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.36.10 (0.182 с.) |
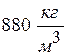 вакуумметр, установленный на его крышке, показывает
вакуумметр, установленный на его крышке, показывает 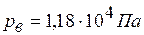 Па (рис.2.4)
Па (рис.2.4) , присоединенного к резервуару на глубине Н=6м от поверхности жидкости, и положение пьезометрической плоскости.
, присоединенного к резервуару на глубине Н=6м от поверхности жидкости, и положение пьезометрической плоскости. 
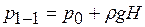 ,
, .
. .
.

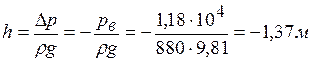
 Задачи для самостоятельного решения.
Задачи для самостоятельного решения.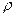 =1200кг/м3? Глубина скважины Н=460м.
=1200кг/м3? Глубина скважины Н=460м. Задача 2.3 [4] На рис.2.6. приведен вертикальный разрез газонефтеводоносного пласта, имеющего выход на земную поверхность в точке А. Найти абсолютное давление в газовой шапке, если Н=2500м, h1=800м, h2=300м, плотность минерализованной воды
Задача 2.3 [4] На рис.2.6. приведен вертикальный разрез газонефтеводоносного пласта, имеющего выход на земную поверхность в точке А. Найти абсолютное давление в газовой шапке, если Н=2500м, h1=800м, h2=300м, плотность минерализованной воды  =1020кг/м3, плотность нефти
=1020кг/м3, плотность нефти 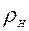 =850кг/м3, атмосферное давление
=850кг/м3, атмосферное давление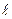 =3м (в направлении, перпендикулярном плоскости чертежа), шириной в=0,7м и высотой Н0=2,5м разделяет бассейн с водой на две части. В левой части поддерживается уровень воды Н1=2м, в правой – Н2=0,8м.
=3м (в направлении, перпендикулярном плоскости чертежа), шириной в=0,7м и высотой Н0=2,5м разделяет бассейн с водой на две части. В левой части поддерживается уровень воды Н1=2м, в правой – Н2=0,8м.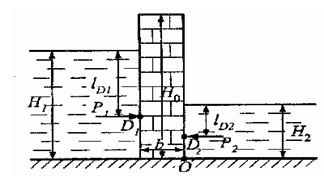
 =2500кг/м3.
=2500кг/м3.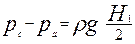 .
.
 .
. , тогда
, тогда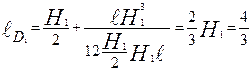 м.
м. кН
кН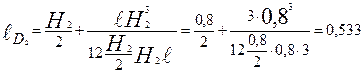 м.
м.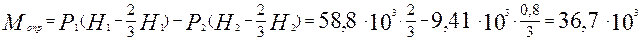 Нм
Нм Нм
Нм
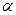 =600, а расстояние от его нижней кромки до оси шарнира а=1,3м. Вес щита можно не учитывать.
=600, а расстояние от его нижней кромки до оси шарнира а=1,3м. Вес щита можно не учитывать. .
. кН.
кН.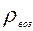 =1,23кг/м3,
=1,23кг/м3,  =0,515кг/м3.
=0,515кг/м3.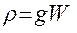

 ;
; м3.
м3.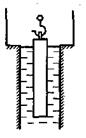 Задача 2.8. Перед подземным ремонтом газовую скважину «задавили», залив ее ствол до устья (до поверхности земли) водой (рис. 2.18). Затем в скважину лебедкой спустили насосно-компрессорные трубы, по которым при эксплуатации скважины поступает из пласта газ.
Задача 2.8. Перед подземным ремонтом газовую скважину «задавили», залив ее ствол до устья (до поверхности земли) водой (рис. 2.18). Затем в скважину лебедкой спустили насосно-компрессорные трубы, по которым при эксплуатации скважины поступает из пласта газ. =740кг/м3) можно залить в железнодорожную цистерну внутренним объемом 50м3 и массой 23т, чтобы она еще сохраняла плавучесть в пресной воде.
=740кг/м3) можно залить в железнодорожную цистерну внутренним объемом 50м3 и массой 23т, чтобы она еще сохраняла плавучесть в пресной воде.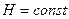 .
. , см
, см
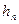 , см
, см
 , см
, см
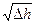
 , (3.19)
, (3.19)
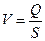 , (3.20)
, (3.20) .
. находим из формулы Дарси - Вейсбаха для определения потерь напора по длине трубопровода:
находим из формулы Дарси - Вейсбаха для определения потерь напора по длине трубопровода: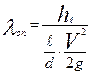 , (3.22)
, (3.22) аналитическим путем. Для этого необходимо вычислить число Рейнольдса по формуле
аналитическим путем. Для этого необходимо вычислить число Рейнольдса по формуле , (3.23)
, (3.23)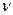 - кинематический коэффициент вязкости жидкости, см2/с; V -средняя скорость движения жидкости в трубопроводе, см/с; d - внутренний диаметр трубопровода, см.
- кинематический коэффициент вязкости жидкости, см2/с; V -средняя скорость движения жидкости в трубопроводе, см/с; d - внутренний диаметр трубопровода, см. ; (3.24)
; (3.24)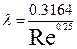 . (3.25)
. (3.25)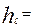 f(V):
f(V):
 , (3.26.)
, (3.26.)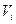 - средняя скорость движения жидкости в i-м сечении;
- средняя скорость движения жидкости в i-м сечении; - площадь живого сечения трубопровода в i - м сечении, см2(см. табл. 3.6).
- площадь живого сечения трубопровода в i - м сечении, см2(см. табл. 3.6).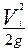 , см.
, см. h в местном сопротивлении:
h в местном сопротивлении: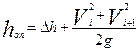 , (3.28)
, (3.28) , (3.29)
, (3.29) , (3.30)
, (3.30) Т
Т
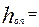 f(Q).
f(Q).


